はじめに
素因数分解のアルゴリズムとして、試し割法やrho法、p-1法、楕円曲線法(ecm)などが有名である。これらの長所短所はよく知られているが、具体的にどのような場合にどのアルゴリズムを(更にはどのパラメータを)使うかはあまり知られていない。例えば、何の情報もない自然数nに対してecmを試すよりも、まずは2や3といった小さい素数で試し割をしてみるだろうし、逆に試し割をある程度行ったならばecmに切り替えた方が効率的だろう。雰囲気はそういうことが知りたいのだが、具体的な境界を示すのはちょっと大変だ。
ここで結論が出ているわけではなく、ああだこうだ言っているだけであることに注意してほしい。
rho法
rho法 自体の説明はリンク先に譲る。
$n$の素因数$p$について、大体$\sqrt{p}$回のループで$p$を発見できることが知られている。理屈の上ではそうなのだが、実験して調べてみる。$k$回のループではどれほどの大きさの$p$が見つかることが期待できるのだろうか?
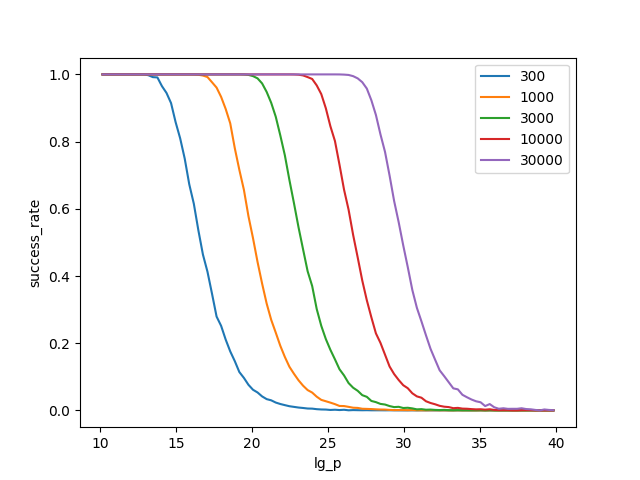
このグラフは、rho法のループ回数を300, 1000, ..., 30000と変化させたとき、大きさ$\lg p$の素因数を発見できる確率を表している。例えば、1000回のループだと、$2^{18}$くらいまでは確実に見つけられるが、そこからどんどん発見確率は下がり、$2^{25}$くらいの素因数を発見できる確率はごくわずかだ。ただしあくまで素因数のサイズとループ回数の関係を知りたいので、失敗は考慮していない。rho法の場合、2つの素因数が近いとき失敗することがあるが、その時は初期値を変えてリトライすればよい。
とは言え、何か閾値を設けないと扱い辛い。そこで、ecmの界隈で利用されているT-levelを参考に、$1-1/e$=約63%を基準としてみよう。つまり、$k$回のループを実行すると63%の確率で見つかる素因数のサイズを見積もりたい。
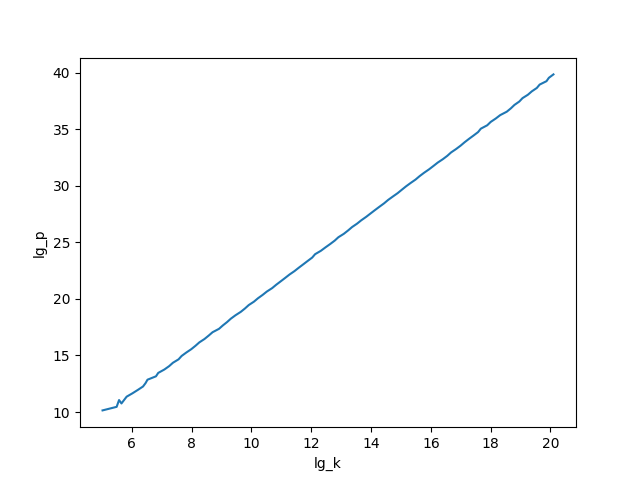
実験結果から$\lg k$と$\lg p$の関係は線形になることが分かる。近似すると、$\lg p = 2\lg k - 0.35$が得られた。$\sqrt{p}$回のループで$p$を発見できるという見積もりは、実証的に間違ってはいないようだ。