非負値テンソル因子分解の更新式の導出と実装

書いたコード

稚拙な出来ですが、Github でコードを公開させていただいています。

参考文献

• [1] 亀岡弘和: 非負値行列因子分解入門 ～音響信号処理を題材として～
  (視覚からNMFを理解できます)
• [2] 澤田宏: 非負値行列因子分解 NMF の基礎とデータ／信号解析への応用
  (わかりやすいNMFの解説記事です)
• [3] 続・わかりやすいパターン認識―教師なし学習入門― (数式の導出でお世話になりました)
• [4] 松林達史他: 非負値テンソル因子分解を用いた購買行動におけるブランド選択分析
  (NTFの実データへの利用方法について述べています)
• [5] Koh Takeuchi et al.: Non-negative Multiple Tensor Factorization
  (拡張NTFの論文ですがNTFの理解にも役立ちます)

文献[1,2,4,5]は今のところネット上で無料公開されているので、自分みたいな貧乏性(論文を自由にダウンロードできない方)には超おすすめです。特に、非負値テンソル因子分解(Non-negative Tensor Factorization, 以下NTF)の前に非負値行列因子分解(Non-negative Matrix Factorization, 以下NMF)がよくわからないという方には文献[1][2]がとてもわかりやすいので、本記事の前に一読することをすすめます。文献[3]は数式展開がとても丁寧で、ベイズ推定の本の中では最高にわかりやすく、これもおすすめです。

自分の雑な理解

非負値テンソル因子分解改めNTFはテンソルを低ランクの非負値のテンソル積で近似する分解計算である。誤解を恐れずに高校生レベルでいいかえると、大きなサイズの行列を各成分が 0 以上である小さなサイズの行列に因数分解することである。テンソルとはスカラー、ベクトル、行列の概念の拡張であり、これらはそれぞれ0階のテンソル、1階のテンソル、2階のテンソルと言い換えられる。様々な研究分野で広く使われているNMFは2階のテンソルに限定したNTFのことである。

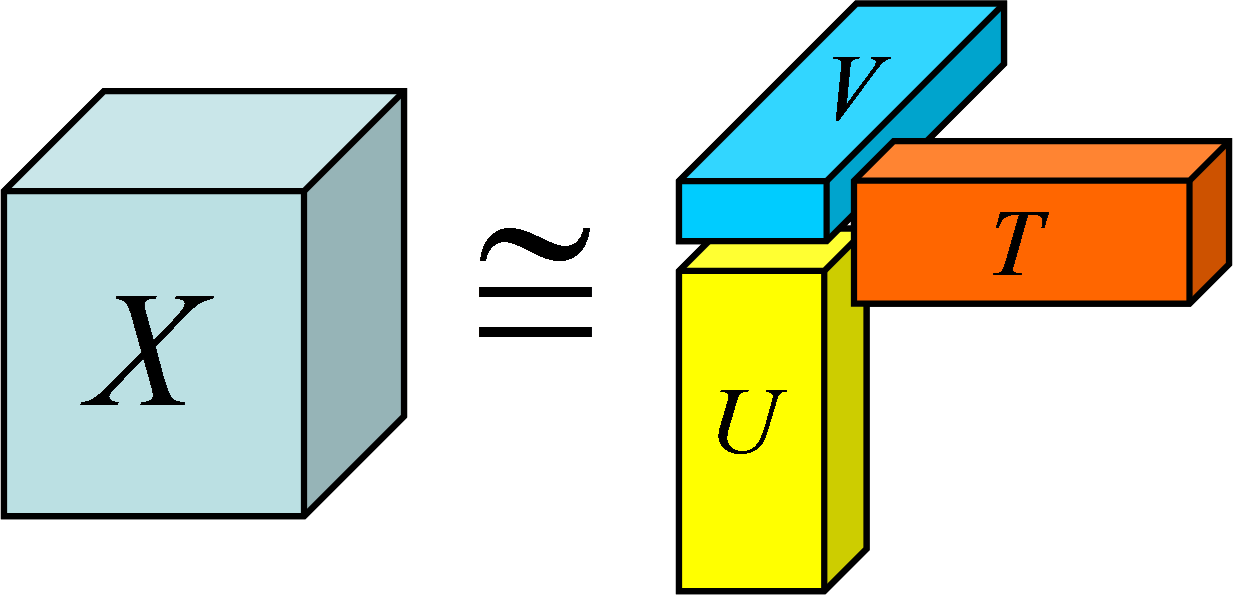
人間が一見するだけはわからない膨大なデータも、NTFを適用して低ランクのテンソルに分解することで複数の因子間の関係を抽出でき、人間にとってわかりやすいデータ形式となる。直感的な理解のために、3階のテンソル $X$ を階数の低い3つのテンソル $T,U,V$ (行列、ベクトル etc.)へ近似的に分解できることを表したポンチ絵を以下に示す。

NMFでは2次元のデータにおける因子間の関係しか抽出できなかった。一方、NTFはテンソルの階数だけ因子間の関係を抽出できるため、より複雑な関係を分析することが可能である。これは4次元以上の視覚化が難しいデータを傾向という形で間接的に視覚化できることも意味する。

NTFは元のテンソルと、近似ベクトルの積から再構成したテンソルとの距離(コスト関数)の最小化に基いて行われる。この距離の最小化を解くにあたってはどんな手法を利用しても構わないが、近似テンソルの期待値計算とこれを用いたときのコスト関数の最小化を繰り返すことで、解が効率的に収束する(テンソル分解でありがちな逆行列の計算をしなくてよい!)ことが知られており、しばしばこのアプローチが用いられる。つまり、実務的には、この更新式さえ知っていればNTFを使ってのデータ分析ができるようになる。

更新式の導出

NTFをはじめ機械学習をただのツールとして使う側にとって、このあたりの数式を変換していく過程は疎かにされがちですが、データの特性に応じたコスト関数の設計やモデル化によるアルゴリズムの拡張を扱う上では必須の知識です。なので、自分なりの理解で数式を頑張って展開してみました。

大筋をいうと、コスト関数を偏微分したものが 0 となるとき、コスト関数の極小値をとることを利用して更新式を導出します。

コスト関数の定義

コスト関数にはよく $\beta$ ダイバージェンスが用いられるが、今回はその特別な形式である一般化KLダイバージェンスを取り上げる。$R$ 階のテンソルを分解して得られるベクトルを$u_{ki_{r}}^{(r)}$ とする$(k = 1,2,...,K)$$(i_{r} = 1,2,...,I_{r})$$(r = 1,2,...,R)$。ここで、$K$は基底数(近似に用いる各次元のベクトル数)、$I_{r}$ は各ベクトルの要素数とする。$i_{r}$ は各ベクトルの要素への添字とする。$L$ を各次元の要素数の集合としたとき、ベクトルのクロネッカー積で得られるテンソルは次式となる。

\hat{x}_{\bf i} = \sum_{k=1}^{K} \prod_{r=1}^{R}
u_{ki_{r}}^{(r)}
\quad ({\bf i} = i_{1}i_{2}...i_{R} \in L) \quad (1)

一般化KLダイバージェンスに基づくコスト関数は次式のとおり。

D(X, \hat{X})
 = \sum_{{\bf i} \in L}(
   x_{\bf i}\log\frac{x_{\bf i}}{\hat{x}_{\bf i}}
    - x_{\bf i} + \hat{x}_{\bf i}) \quad (2)

近似したいテンソル $X$ と近似したテンソル $\hat{X}$ が完全に一致するとき、本コスト関数は 0 となる。式(1)を式(2)に代入して $\log$ の分数を和に変換すると次式を得られる。

D(X, \hat{X})
 = \sum_{{\bf i} \in L}(
   x_{\bf i}\log x_{\bf i}
   - x_{\bf i}\log \sum_{k=1}^{K}
   \prod_{r=1}^{R} u_{ki_{r}}^{(r)}
   - x_{\bf i} + \sum_{k=1}^{K}
   \prod_{r=1}^{R} u_{ki_{r}}^{(r)}) \quad (3)

コスト関数の偏微分

式(3)を $u_{ki_{r}}^{(r)}$ でサクっと偏微分したいところだが、第二項がlog-sum ( $\log\sum_{k}f_{k}(u_{k{\bf i}})$ ) の形となるため偏微分が難しい。そこで、

h_{k{\bf i}}^{0} = \frac{
  \prod_{r=1}^{R} u_{ki_{r}}^{0(r)}
}{
  \hat{x}_{\bf i}^{0}
} \quad (4)

という $\sum_{k=1}^{K} h_{k{\bf i}} = 1, h_{k{\bf i}} \geq 0$となる性質を持つ変数を定義する。ここで各変数の右肩の 0 は更新前であることを示す。式(3)の第二項に対して式(4)から構成される $h_{k{\bf i}}/h_{k{\bf i}}(=1)$ を積算し Jensen の不等式を用いることで、以下のようにsum-log ( $\sum_{k}\log f_{k}(u_{k{\bf i}})$ )の形をもつ第二項の上限値を導出できる。

- x_{\bf i} \log \sum_{k=1}^{K}
h_{k{\bf i}}^{0}
\frac{\prod_{r=1}^{R} u_{ki_{r}}^{(r)}}
{h_{k{\bf i}}^{0}} \leq - x_{\bf i}
\sum h_{k{\bf i}}^{0} \log
\frac{\prod_{r=1}^{R} u_{ki_{r}}^{(r)}}
{h_{k{\bf i}}^{0}} \quad (5)

式(5)を式(3)に代入することで次式のようなコスト関数の上限値を導出できる。

D(X, \hat{X}) \leq
\sum_{{\bf i} \in L}(
  x_{\bf i}\log x_{\bf i}
  - x_{\bf i} \sum h_{k{\bf i}}^{0} \log \frac{\prod_{r=1}^{R} u_{ki_{r}}^{(r)}}
  {h_{k{\bf i}}^{0}}
  - x_{\bf i} + \sum_{k=1}^{K}
  \prod_{r=1}^{R} u_{ki_{r}}^{(r)}) \\
  = \sum_{{\bf i} \in L}(
    - x_{\bf i} \sum h_{k{\bf i}} \log \prod_{r=1}^{R} u_{ki_{r}}^{(r)}
    + \sum_{k=1}^{K}
    \prod_{r=1}^{R} u_{ki_{r}}^{(r)}
   + C)
   \quad (6)

ここで、$u_{ki_{r}}^{(r)}$ を含まない項については次の偏微分の過程で 0 となるため、$C$ という定数項でまとめた。このコスト関数の上限値を最小化するために、式(6)を $u_{ki_{r}}^{(r)}$ で偏微分したものを 0 とおくと次式が得られる。

0 = \sum_{{\bf i} \in L_{-r}} (
  - x_{\bf i}
\frac{h_{k{\bf i}}^{0}}{u_{ki_{r}}^{(r)}} +
\prod_{\substack{r=1 \\ \bar{r} \neq r} }^{R}
u_{ki_{\bar{r}}}^{(\bar{r})}
) \quad (7)

ここで、$L_{-r}$ は( $\bar{\bf i} = i_{1}...i_{r-1}i_{r+1}...i_{R} \in L_{-r}$ )という集合である。式(7)を式(4)も用いて $u_{ki_{r}}^{(r)}$ について整理することで次の更新式が得られる。

u_{ki_{r}}^{(r)} = u_{ki_{r}}^{0(r)} \cdot
\frac{
  \sum_{\bar{\bf i} \in L_{-r}}
  (x_{\bar{\bf i}}
    / \hat{x}_{\bar{\bf i}}^{0})
    \prod_{\substack{\bar{r}=1 \\ \bar{r} \neq r} }^{R}
    u_{ki_{\bar{r}}}^{0(\bar{r})}
}{
  \sum_{\bar{\bf i} \in L_{-r}}
  \prod_{\substack{\bar{r}=1 \\ \bar{r} \neq r} }^{R}
  u_{ki_{\bar{r}}}^{(\bar{r})}
} \quad (8)

コスト関数の上限値を最小化して得られた $u_{ki_{r}}^{(r)}$ を$h_{k{\bf i}}^{0}$ として、さらにコスト関数の上限値を最小化するという逐次更新によって、$D(X, \hat{X})$ の極小値が得られる。極小値が得られた時点での ${\bf u}_{k}^{(r)}$ が元のテンソルを因子分解して得られる近似テンソルである。

実装

Python + Numpy で実装しました。足りないライブラリはpipで落としてきてください。Python + Numpy を初めて触る人には最初からいろいろパッケージが入っている Anaconda を利用するのがハマりづらくておすすめです。

入力するデータを行列とすれば、2階のテンソルのNTF、すなわちNMFも可能です。肝となる更新式の部分だけコードを示しておきます。

ntf.py

class NTF():
    # その他のメンバ関数等はいろいろ省略...
    def updateBasedOnGKLD(self, x, factor, index):
        # Create tensor partly.
        element = self.kronAlongIndex(factor, index)

        # Summation
        element = element.reshape(self.preshape[index])
        estimation = self.createTensorFromFactors()
        boost = x/(estimation + EPS)
        numer = self.sumAlongIndex(boost*element, factor, index)
        denom = np.sum(element)

        return numer/(denom + EPS)

    def kronAlongIndex(self, factor, index):
            element = np.array([1])
            for i1 in factor[:index]:
                element = np.kron(element, i1)
            for i1 in factor[index + 1:]:
                element = np.kron(element, i1)
            return element

    def sumAlongIndex(self, value, factor, index):
        for _ in np.arange(index):
            value = np.sum(value, axis=0)
        for _ in np.arange(index + 1, len(factor)):
            value = np.sum(value, axis=1)
        return value

    def createTensorFromFactors(self):
        tensor = self.composeTensor(self.factor)
        tensor = np.sum(tensor, axis=0)
        return tensor.reshape(self.shape)

    # composeTensor の実体となる関数。
    def composeTensorSerially(self, element):
        return map(self.kronAll, element)

    def kronAll(self, factor):
        element = np.array([1])
        for i1 in factor:
            element = np.kron(element, i1)
        return element

Pythonなのにfor文が多くて汚い感じがしますが、ここでこだわるのも微妙なので放置しています。
# キレイな書き方 or 爆速で動く書き方を知っていたらプルリクください。

実験

ガウス分布から作成した乱数をクラスタリングする実験(というよりデモ)をしました。

実験条件

以下の2つのガウス分布に基づいてそれぞれ 100 サンプル3次元空間に散布しました。

ID	平均	分散
A	(10, 10, 20)	$5 \times E_{3}$
B	(30, 30, 30)	$5 \times E_{3}$

既に2つのクラスタからサンプルが撒かれていることがわかっている体で、マッチポンプ的ですが基底数は2とします。つまり、3階テンソルを基底数2で近似ベクトルに分解することになります。

追試するには run_ntf_demo_3rd_order_2bases.py を実行してください。なお、異なるパラメータ(e.g., テンソルの階数、基底数 etc.)で同様の実験を試行できるコードも run_ntf_demo_*.py といった名前で用意しています。

結果

下図の右側に近似ベクトルからクロネッカー積で再構成したサンプルの分布(テンソル)を示します。比較のために左側に元のサンプルの分布も示しておきます。各軸に割り振られている値は分割したビンごとへの添字なので、実験条件で示した平均と分数とは一致しない点だけご注意ください。

元のサンプルの分布	近似ベクトルから再構成したサンプルの分布

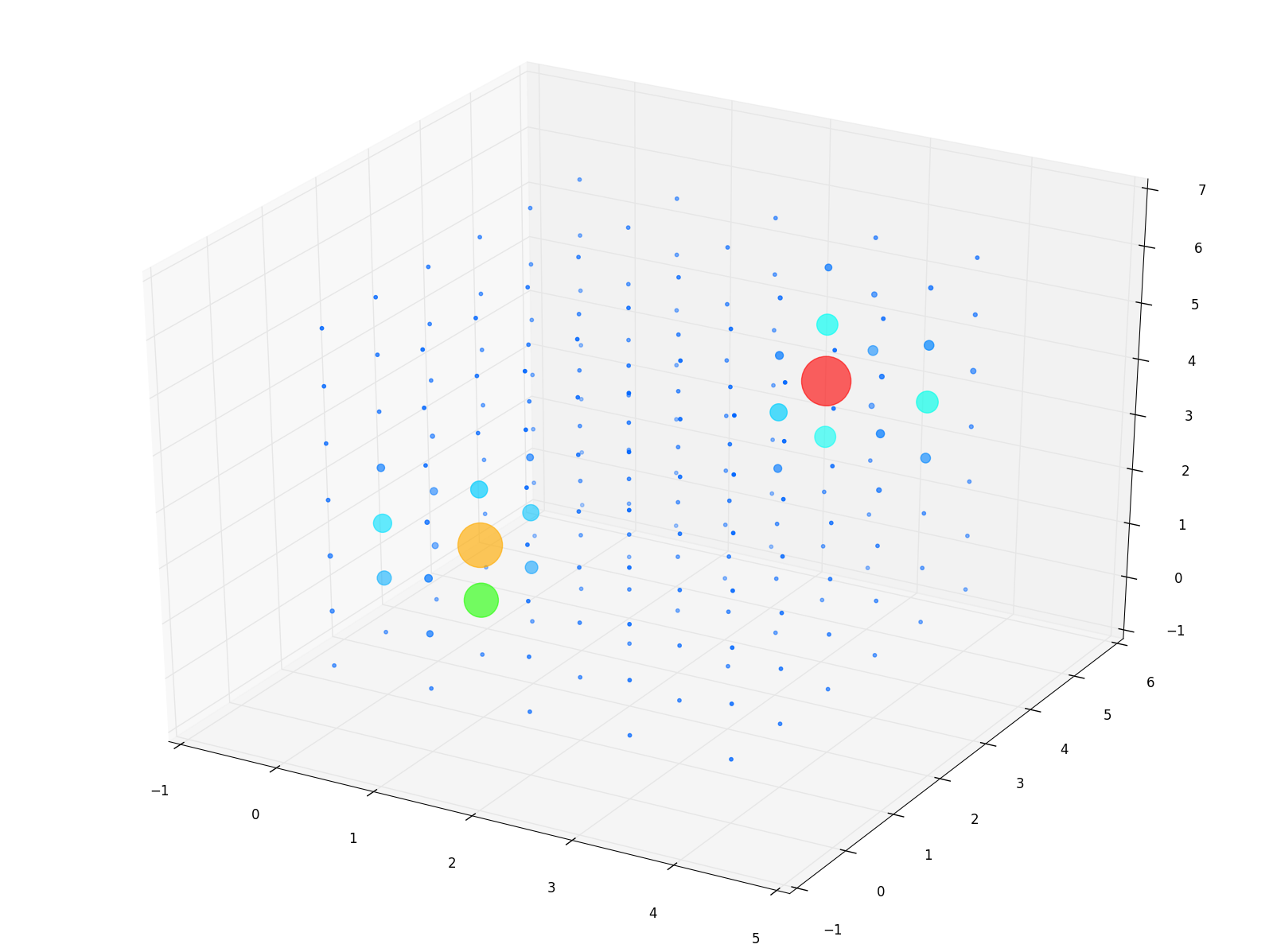両方のサンプルの分布が近いことがわかります。なお、サンプルの分布の再構成に用いた近似ベクトルは以下のようになりました。

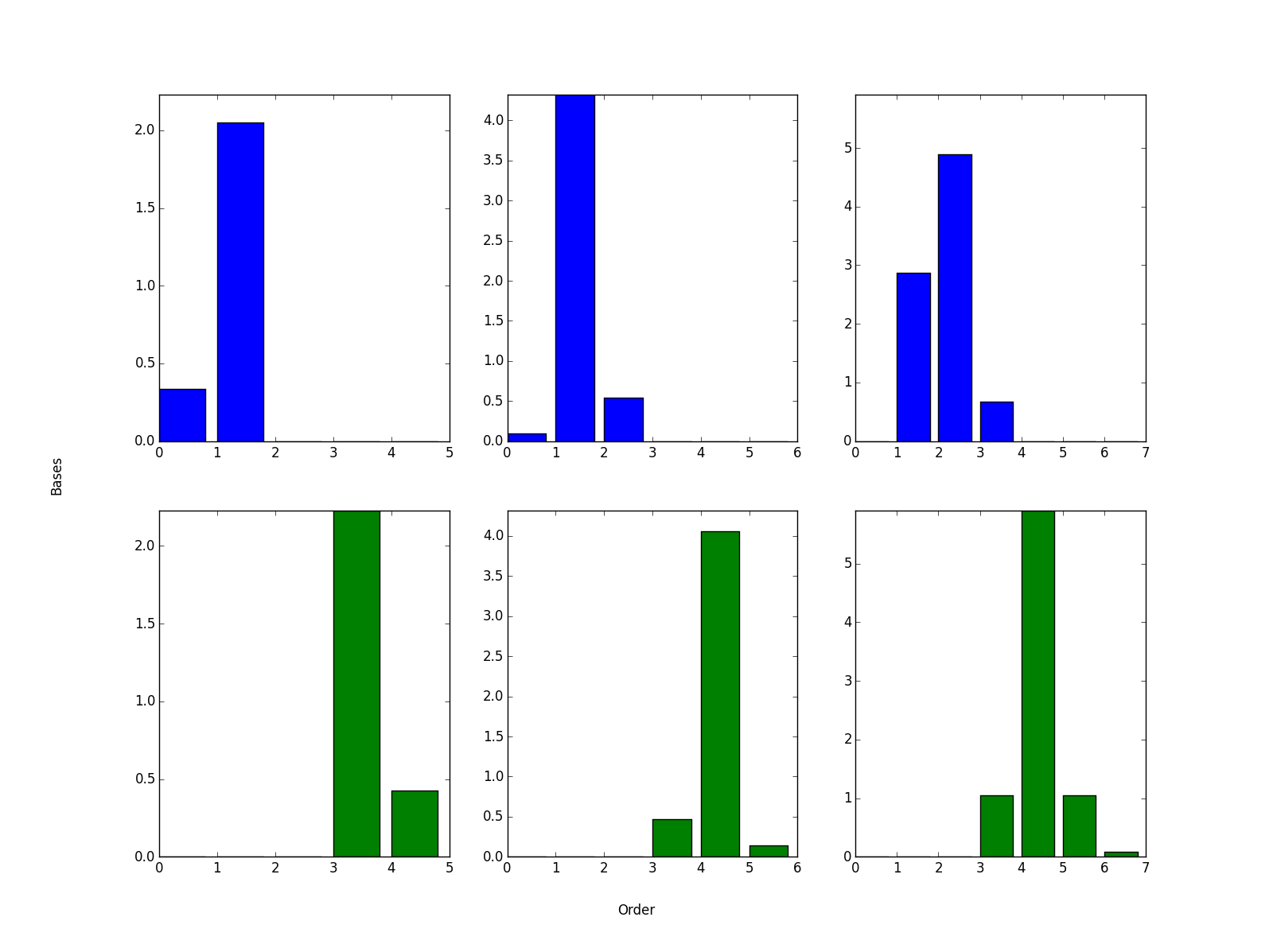
横軸は因子の軸です。縦軸が基底の軸なのですが、各基底に1つのガウス分布が分配されていることがわかります。とまあこんなかんじで、それなりにコードが組めていることを確認できました。

補足

NTFをクーポンの購買履歴に適用しました。より実用的な例ですので、よければこちらもご覧ください。