書いたコード
稚拙な出来ですが、Github でコードを公開させていただいています。
補足
非負値テンソル因子分解(以下、NTF)とはなんぞや? という方はNTFの概要と更新式の導出と簡単なデモを記載しましたので、こちらもご覧ください。NTF以前に非負値行列因子分解(以下、NMF)がよくわからないって方にも、記載した参考文献が役立つと信じています。
クーポンの購買データへの適用
去年 Kaggle で催されたリクルートのクーポン購買予測コンペのデータにNTFを適用してみました。
実験条件
本記事では以下の2種類の実験の試行について述べます。
-
(実験1): 「クーポンジャンル」、「購入者の性別」、「クーポン発行元の都道府県」の
因子から構成した3階のテンソルを基底数5で分解する。 -
(実験2): さらに「購入者の年齢」、「割引後の価格」の因子を加えて構成した
5階のテンソルを基底数8で分解する。
これら実験で使われている各因子の具体的な水準は以下の表のとおりです。
| 因子名 | 水準の数 | 水準 |
|---|---|---|
| クーポンジャンル | 13 | 00 グルメ, 01 エステ, 02 ビューティー, 03 ネイル・アイ, 04 ヘアサロン, 05 健康・医療, 06 リラクゼーション, 07 レジャー, 08 ホテル・旅館, 09 レッスン, 10 宅配, 11 ギフトカード, 12 その他のクーポン |
| 購入者の性別 | 2 | 00 男性, 01 女性 |
| 発行元の都道府県 | 47 | 00 北海道, 01 青森県, 02 岩手県, 03 宮城県, 04 秋田県, 05 山形県, 06 福島県, 07 茨城県, 08 栃木県, 09 群馬県, 10 埼玉県, 11 千葉県, 12 東京都, 13 神奈川県, 14 新潟県, 15 富山県, 16 石川県, 17 福井県, 18 山梨県, 19 長野県, 20 岐阜県, 21 静岡県, 22 愛知県, 23 三重県, 24 滋賀県, 25 京都府, 26 大阪府, 27 兵庫県, 28 奈良県, 29 和歌山県, 30 鳥取県, 31 島根県, 32 岡山県, 33 広島県, 34 山口県, 35 徳島県, 36 香川県, 37 愛媛県, 38 高知県, 39 福岡県, 40 佐賀県, 41 長崎県, 42 熊本県, 43 大分県, 44 宮崎県, 45 鹿児島県, 46 沖縄県 |
| 購入者の年齢 | 13 | 00 20歳未満, 01 20歳-, 02 25歳-, 03 30歳-, 04 35歳-, 05 40歳-, 06 45歳-, 07 50歳-, 08 55歳-, 09 60歳-, 10 65歳-, 11 70歳-, 12 75歳- |
| 割引後の価格 | 10 | 00 100円未満, 01 100円-, 02 1000円-, 03 2000円-, 04 3000円-, 05 5000円-, 06 10000円-, 07 20000円-, 08 30000円-, 09 50000円- |
「購入者の年齢」と「割引後の価格」については One-hot 表現にするためにデータの分布を眺めてから適度に量子化しています。なお、ざっくりとしたデータの分布や傾向を眺めたい人には有志によって可視化された因子間の関係をどうぞ。
追試するためには、コードの実行前にKaggle から取得できるコンペ用のデータ(Kaggle へのログインが必要です) を unzip したものを data/ 以下に配置する必要があります。データを配置後、実験1を追試するには run_ntf_ponpare_coupon_3rd_order.py、実験2を追試するには run_ntf_ponpare_coupon_5th_order.py をそれぞれ実行してください。
結果
実験1: 3階のテンソルの因子分解の結果
分解された近似ベクトルと比較するために、元のテンソルであるクーポンの購買データの分布を示しておきます。
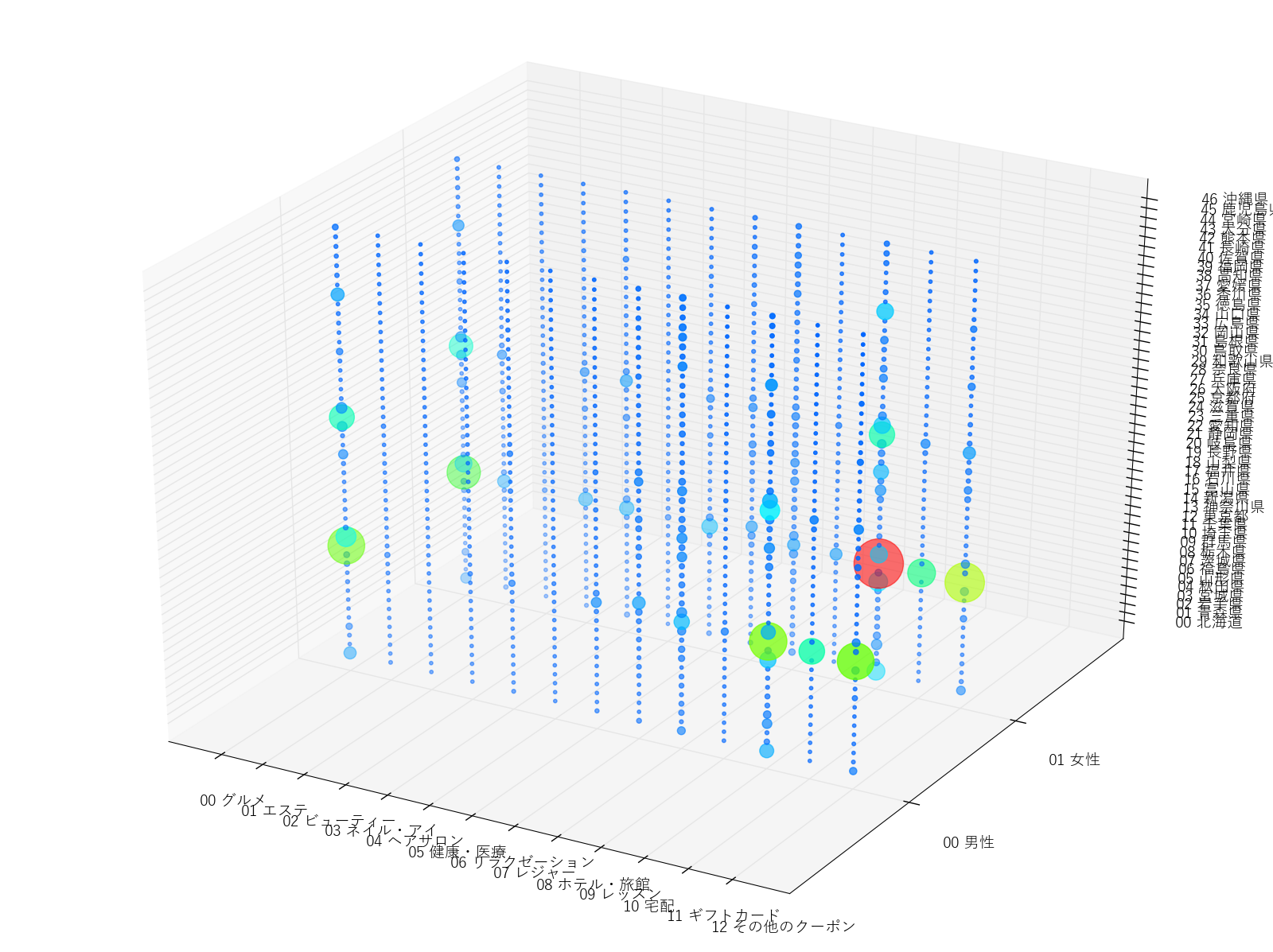
実験1で用いる分布は3次元データなので上図のように俯瞰が可能ですが、1,2次元のデータと比べて傾向をつかむことが難しいことは明らかです。それを踏まえて、因子分解で得られた近似ベクトル(下図)をみてみます。
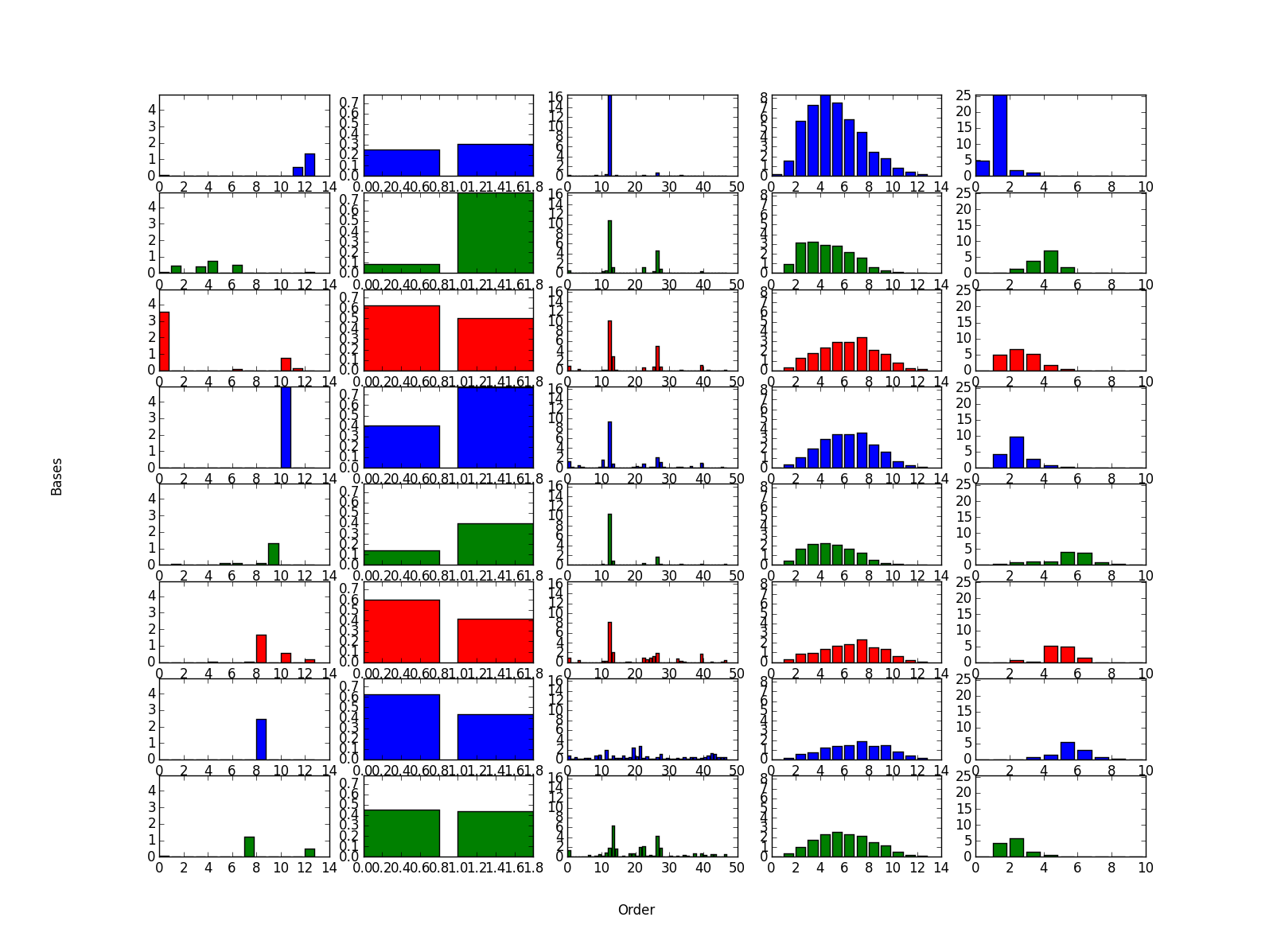
横軸は因子の軸であり、表で上から列挙した順に左から並んでいます。縦軸は基底の軸であり、各基底をデータ傾向として見なせます。3次元のデータではパッと見てわからなかった傾向がつかみやすくなっています。
上図に示された各基底の近似ベクトルから読み取れる傾向を、上から順に述べていきます。
| ID | 傾向 |
|---|---|
| 1 | 東京在住の女性のクーポンの利用傾向が顕著にでている。 |
| 2 | 全国的に男性はホテル旅館のクーポンを利用している。レジャーのクーポンの利用もそこそこ多い。都市部近郊の利用者が多め。 |
| 3 | 全国的に女性は宅配サービスを利用している。 |
| 4 | 全国的に男性はホテル旅館のクーポンを利用している。2.と比べてレジャーのクーポンの利用が見えなく、利用者も地方に散っている。 |
| 5 | 東京を除く都市部の利用者には男女問わず、グルメのクーポンは人気が高そう。 |
各基底からクーポンの購買の傾向をそれなりに読み取ることができますが、少し雑に傾向が出ていることは否めません。特に、1つ目の傾向はかなり雑で、本来分かれていてほしいヘアサロンなどの美容関係のクーポンの傾向が包含されてしまっています。
実験2: 5階のテンソルの因子分解の結果
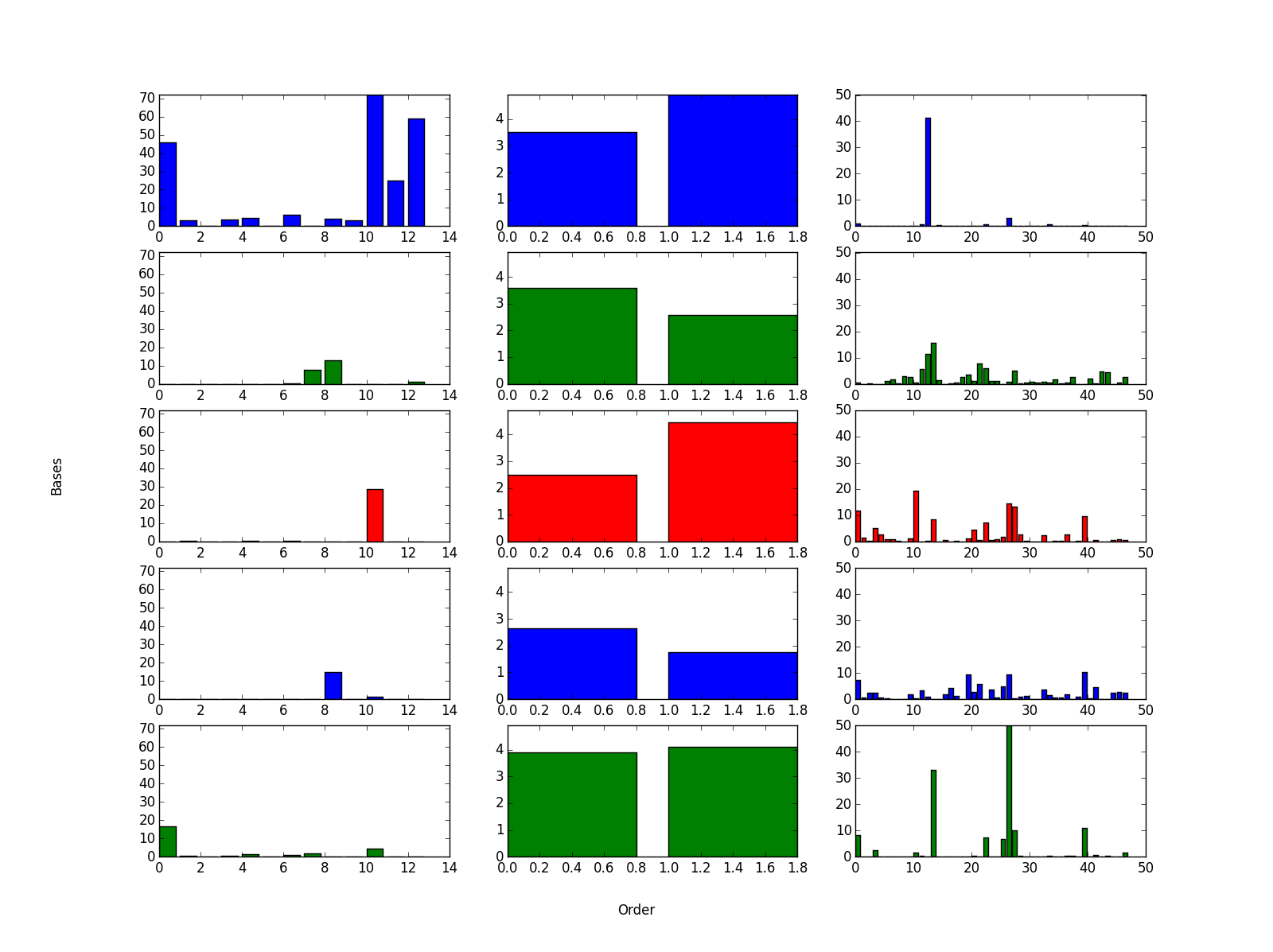
実験1と異なり、5次元のデータを扱っているため、元のテンソルの視覚化は困難なのでスルーです。というわけで、いきなり因子分解で得られた近似ベクトル(下図)をみてみます。
続けて、上図に示された各基底の近似ベクトルから読み取れる傾向を、上から順に述べていきます。
| ID | 傾向 |
|---|---|
| 1 | ギフトカードやその他のクーポンは爆安なものに人気が集中している。そして、購入者が東京在住の人ばかり。 |
| 2 | ヘアサロンなどの美容関係の利用者は若年層の女性に集中している。3000-5000円台が人気があるっぽい。 |
| 3 | グルメのクーポンの利用者は若干男性が多め。中年層で人気。他のクーポンジャンルと比べて割りと大阪の利用者が多い。 |
| 4 | 1000-2000円台の宅配サービスが中年層の女性に人気。 |
| 5 | レッスンのクーポンが若年層の女性に人気。値段の幅が他に比べて広め。 |
| 6 | ホテル旅館の利用者の傾向が示されている。東京在住の利用者が多いのと、人気の価格帯が3000-10000円台なので、地方へのお泊り出張者の利用を表している? |
| 7 | 上に同じくホテル旅館の利用者の傾向でているが、地方の利用者が多いのと、人気の価格帯が5000-20000円台なので、こっちは旅行の宿泊先としての利用者が多いことを示している? |
| 8 | レジャーで利用する人は全国的に散っている印象。1000-2000円台のチケットが人気。 |
実験1のときより基底数とテンソルを構成する因子の数を増やしたことで、クーポンの利用傾向が細かく出ていることがわかります。特に、実験1では他の傾向と包含されてはっきりわからなかったヘアサロンなどの美容関係が、実験2でははっきりと2つ目の基底で傾向が出ています。視覚化が困難な高次元のデータも、NTFなら各因子を関連づけなから視覚化することができます。
考察
NMFのように2つの因子間にとどまらず、複数の因子間の複雑な傾向をみれるところがNTFの良さであり、NMFとの差分です。実験1のときよりも実験2のときのほうが細かなクーポンの購買の傾向を把握できたように、理論的には、分析する因子の数(テンソルの階数)を増やすほど複雑な因子間の関係を可視化でき、基底数を増やすほど多様な傾向を抽出することができます。
以上から、自分はテンソルの階数と基底数を増やすことで、クーポンの購買データからいろんな県民性が浮き彫りになることを期待していました。が、人生そんなに甘くなく、実際いろいろ実験していると以下のような問題に直面しました。
- 固定のデータ数に対してテンソルの階数を大きくするとスパースになる
NTFのことを知るきっかけとなった方(「さいごに」の章で少し言及します)から「テンソルの階数が大きくなると、分析するデータ空間(テンソル)がスパースになるので因子分解がうまくいかない」という話を伺いましたが、確かにごもっともです。かなり直感的ですが、平面に撒かれたゴマと3次元空間に撒かれたゴマでは、どちらがかき集めるのが大変そうかを考えれば、後者なのは明らかです。なので、本記事のクーポンの購買データへ適用した実験では、適度に量子化するなどしてデータ空間を限定したりしています。なお、NTFの概要を述べた記事で挙げた文献[5]では、この問題を解消するためにデータを稼ぐような工夫をいれたNTFを提案しています。 - テンソルの階数に応じて計算コストが指数的に高くなる
run_ntf_ponpare_coupon_7th_order.py という 7階テンソルを分析するコードも用意していますが、自分の計算機(数年前にドスパラで購入した10万しなかったデスクトップ)ではなかなか収束しなさそうだったので実験をあきらめました。各基底の期待値計算などは並列計算可能なので、今流行のCUDAとか利用すれば計算時間を短縮することはできそうですが、さらにテンソルの階数が増えると手に負えなくなることは容易に想像できます。 - 基底を増やすほど全基底の直交性を維持することが難しくなる
NMF にも当てはまる問題です。本記事では取り上げませんが、NTFやNMFの初期値への依存が高い問題もこれに含まれます。これを解決するアプローチとして、分析するデータの前提に基づいた基底ごとの分布のモデル化や、収束過程における制約の導入、データが十分に存在する部分におけるコスト関数への重み付けなど、様々な方法が考えられます。また、適切な基底数を指定することも重要です。これには、分割ルールの集中度によって基底数を決めるノンパラメトリックベイズや、もう少し簡単な凸クラスタリング法のような基底数ではなく全基底の分散を既知とする方法へ拡張するアプローチが有効です。単純ですが、試行を重ねてAICなどの情報量基準に基いて基底数を決定するのもありだと思います。
自分のようなNTFをただ使う側の方も、これらは注意事項として把握しておくと良いかもしれません。
さいごに
NTTオープンハウス2015のポスター発表を見てNTFというものを知り、NMFより高次元なデータの関連性を俯瞰できそうと期待して勉強に至りました。本記事は、NTFのことをいろんな人に知ってもらいたいというより、説明することで自分自身の理解を高めることと、識者から意見をもらいたいというを動機で書いています。もちろん、NTFの概要を述べた記事とあわせて本記事が「NMFは知っているがNTFとはなんぞや?」という方々の酒の肴になることや、機械学習の初学者(特に学生)の助けになることは願ってもない幸いです。
ポスター発表者の方々とNTFやその他の技術についてお話できたことを感謝します。機械学習と無縁な1企業の平社員の自分は、知識不足のためにいくつか素っ頓狂な質問もしてしまいましたが、丁寧なご回答をいただけました。参加者の多くが超一流の研究者ばかりで恐縮でしたが、機械学習を学んでいく上での良い刺激となりました。本当にありがたいことです。
発表の情報をたよりにコードを組んだり、更新式の導出過程を書いて説明することで、NTFについて理解を深めることができました。次は無限次元行列の確率モデルを用いたデータ解析のようなデータを矩形分割するコードを作成してみたいと思います。