書いたコード
稚拙な出来ですが、Github でコードを公開させていただきました。
参考文献
- [1] 続・わかりやすいパターン認識―教師なし学習入門― (とてもわかりやすい本!)
- [2] D. Lashkari and P. Golland: Convex clustering with exemplar-based models (凸クラスタリング法の原著)
自分の雑な理解
凸クラスタリング法は混合正規分布のパラメータ推定をベースとしたクラス数を既知としないクラスタリング手法である。
通常のEMアルゴリズムによる混合正規分布のパラメータ推定(以下、soft K-means)との違いは初期値を割り振らないといけないパラメータにある。
| 手法 | 初期値 |
|---|---|
| soft K-means | 正規分布の数と各分布の平均 |
| 凸クラスタリング法 | 正規分布の分散(全分布で統一) |
ようするに、soft K-means よりも解の初期値への依存が小さいことが利点である。
観測データ全てをセントロイドとみなして、各セントロイドが形成する正規分布の尤度を計算する。尤度計算は最初の一回きりであり、事前確率のみを更新していく。更新により、分布を形成しがたいセントロイドの事前確率はゼロへと近づく。一定の事前確率で足きりしても、なお残ったセントロイドの数が最終的なクラス数となる。
実装の動機
文献[1]で紹介されていて興味を持った。実装が簡単そうなのと、初期値への依存が低そうなのが魅力的。自分の趣味のおもちゃ作りのアプローチとして、ノンパラメトリックベイズより手軽に使えるのではと期待して実験してみた。
実装
Python + Numpy で実装した。
凸クラスタリング法のパラメータ更新の実装部のみを示す。
def calculateLikelihoodCombination(x, sigma, gaussianFunc):
likelihood = np.empty(0)
for i1 in x:
likelihood = np.append(likelihood, gaussianFunc(x, i1, sigma))
samples = len(x)
return np.reshape(likelihood, (samples, samples))
def calculatePrior(prePrior, likelihood):
samples = len(prePrior)
molecule = (prePrior*likelihood.T).T
denomin = np.sum(molecule, axis=0) + 1e-10
return np.sum(molecule/denomin, axis=1)/samples
def runConvexClustering(x, hyperSigma, gaussian, plotter):
# Pre-calculation of likelihood
likelihood = calculateLikelihoodCombination(x, hyperSigma, gaussian)
# Initialize prior probability.
classNum = len(x) # Number of samples is used as number of classes.
firstPrior = 1.0/classNum # Set non zero value.
prior = np.repeat(firstPrior, classNum)
# Update parameters.
for dummy in range(1000):
prior = calculatePrior(prior, likelihood)
なんと、数十行で済むお手軽さ。
過去にローカルで書いた soft K-means のコードよりも短い気がする。
実験条件
| 因子 | 水準 |
|---|---|
| データ | $\mathbb{R}^{1}$(1次元データ)、$\mathbb{R}^{2}$(2次元データ) |
| サンプリングに使った正規分布の数 | 4つ |
| 1つの正規分布からのサンプル数 | 100点 |
| 初期値の分散の大きさ(倍率) | 普通(×1)、大きめ(×2)、とても大きい(×10) |
1回の実験での全サンプル数は4*100=400点。
初期値の分散の大きさに添えられた倍率は、サンプリングに用いた正規分布の標準偏差からの倍率。
結果
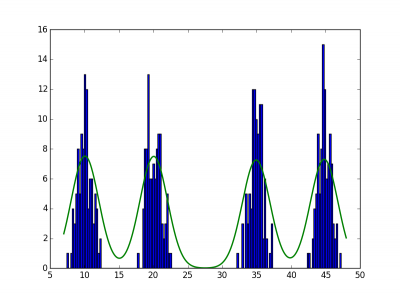
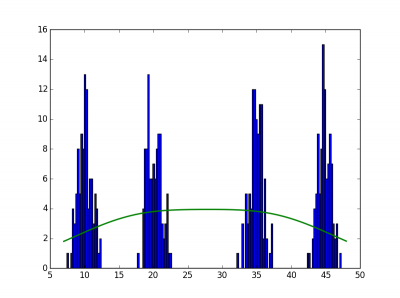
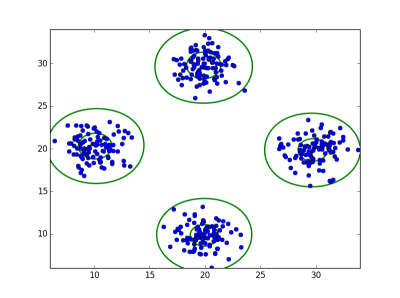
クラスタリングの様子を表した図を以下の表に示す。
表の縦軸はデータ、横軸は初期値の分散の大きさ。
| 普通 | 大きめ | とても大きい | |
|---|---|---|---|
| $\mathbb{R}^{1}$ | 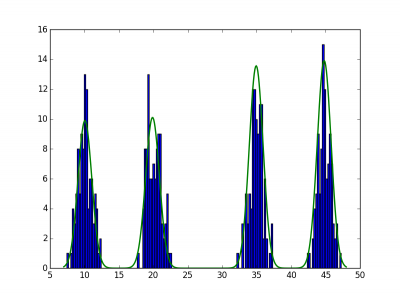 |
 |
 |
| $\mathbb{R}^{2}$ | 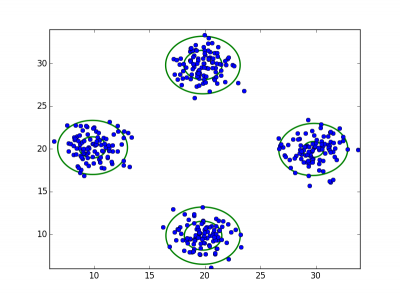 |
 |
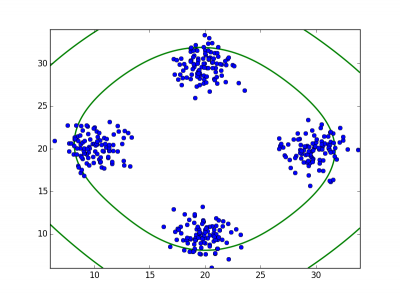 |
青がサンプル、緑が凸クラスタリング法によって求められたクラスのセントロイドから生成した正規分布の凸結合の形状である。
また、足切り後に残ったクラス数は以下のとおり。
同様に、表の縦軸はデータ、横軸は初期値の分散の大きさ。
| 普通 | 大きめ | とても大きい | |
|---|---|---|---|
| $\mathbb{R}^{1}$ | 46 | 40 | 5 |
| $\mathbb{R}^{2}$ | 23 | 11 | 15 |
考察
初期値の分散が[普通、大きめ]のとき、それなりにうまくクラスタリングされている模様。若干、[大きめ]のときのほうが正しくクラスタリングできているような気もする。実問題に適用する場合は想定より少し大きめの分散を使うのが良いかもしれない。初期値の分散が[とても大きい]のとき、4つの分布を1つの分布としてクラスタリングされている。が、これはまあ自明な結果ではある。
1次データより2次データのほうがセントロイドの数がサンプルの生成に用いた正規分布の数(=4)に近い。これについては文献[2]でも言及されている。探索する空間が広いほうが凸クラスタリング法の初期値への依存が小さい性質が生きるとか。ただ、文献[1][2]のようにセントロイドの数が4に十分に近くならなかったことが少々不安ではある。
#実装のバグでないことを切に願う。
まとめ
実装&実験を通して凸クラスタリング法に感じたことは、「実装はとても簡単だが実問題へ適用するにはコツがいりそう」である。文献[1][2]では考察の中で長所や短所が述べられており、扱う問題によっては使いづらい印象がある。コストパフォーマンスの高いクラスタリング法だとは思うが、自分が解きたい問題へのアプローチとして適切かはもう少し慎重に検討したいと思う。