【論文読み】 Graph Structure of Neural Networks (ICML 2020)

Graph Structure of Neural Networks (ICML 2020)

• J. You, J. Leskovec, K. He, and S. Xie, “Graph Structure of Neural Networks,” in Proceedings of the 37th International Conference on Machine Learning, Nov. 2020, pp. 10881–10891. Accessed: Apr. 30, 2022. [Online]. Available: https://proceedings.mlr.press/v119/you20b.html
  • ResNetのKaiming He氏が共著に入っている

論文まとめ

(まとめ方の参考: 高速で論文がバリバリ読める落合先生のフォーマットがいい感じだったのでメモ)

概要

• 畳み込み層における入出力間の接続をRelational Graphとしてモデル化し、精度の良くなる構造 (Sweet Spot) を探索

新規性

• ニューラルネットワークの構造 (Relational Graph) と精度の関係を解明
  • 画像分類の精度を、Relational Graph の平均経路長 (ASPL), クラスタリング係数 (CC) を変数とする滑らかな関数として近似可能

手法の要点

• 同一のRelational Graphをネットワーク内の全ての畳み込み層に適用

有効性の検証

• ランダムグラフを基にRelational Graphを生成し、それらをResNet等に適用してImageNetの分類精度を評価

議論

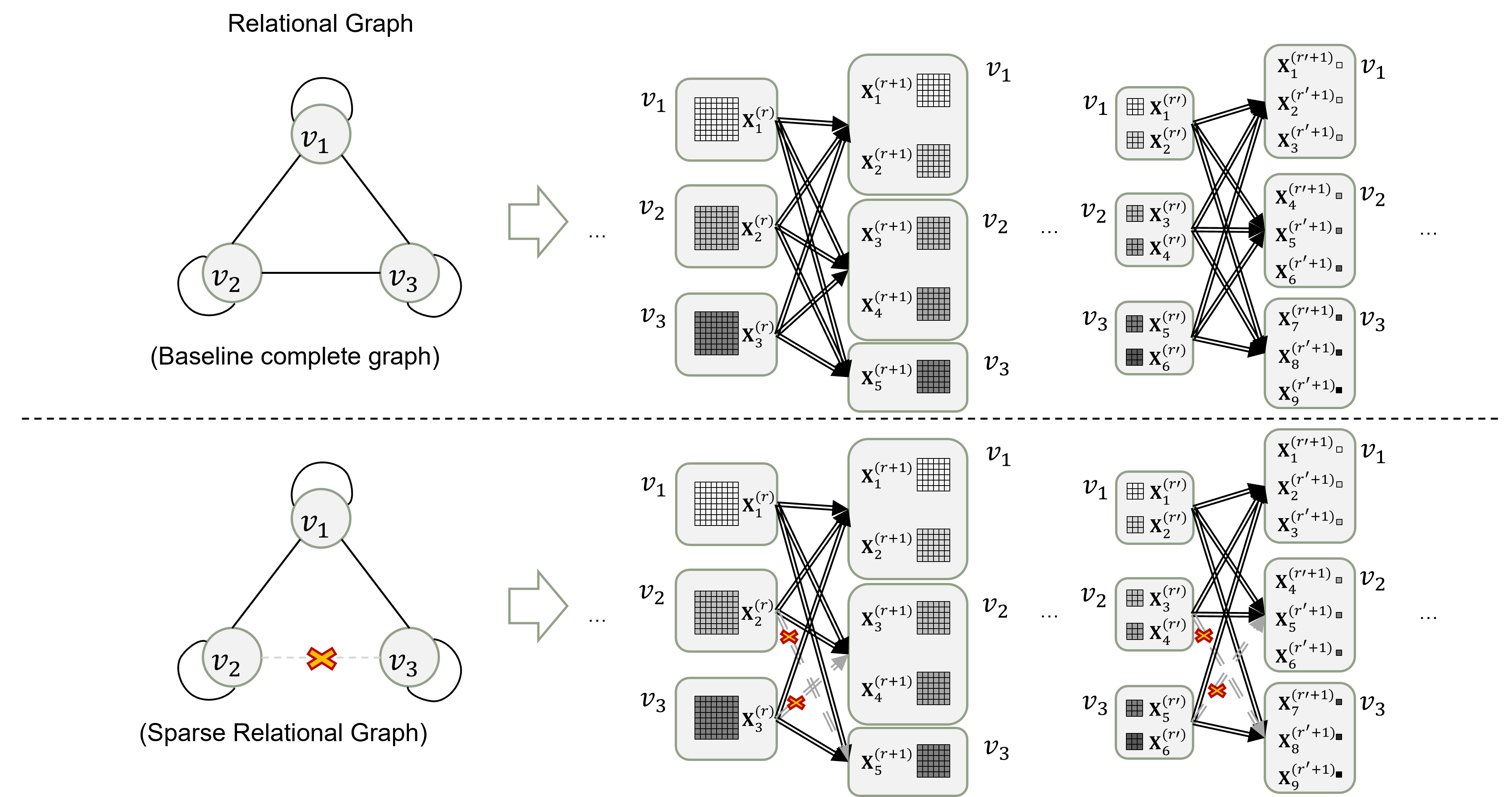
• (完全グラフを基にしたRelational Graphに対応する) Baselineのネットワークより、スパース化されたランダムなRelational Graphを適用したネットワークの方が、最終的なテスト精度が良くなる

次に読むべき論文

(Neural Architecture Search 関連で、ネットワークの最適化に焦点を当ててそうなもの)

• [1]A. Goulas, F. Damicelli, and C. C. Hilgetag, “Bio-instantiated recurrent neural networks.” bioRxiv, p. 2021.01.22.427744, Apr. 24, 2021. doi: 10.1101/2021.01.22.427744. (https://doi.org/10.1101/2021.01.22.427744)
• [2]Á. L. García-Arias, M. Hashimoto, M. Motomura, and J. Yu, “Hidden-Fold Networks: Random Recurrent Residuals Using Sparse Supermasks.” arXiv, Nov. 24, 2021. Accessed: Jun. 13, 2022. [Online]. Available: http://arxiv.org/abs/2111.12330
• [3]U. Evci, T. Gale, J. Menick, P. S. Castro, and E. Elsen, “Rigging the Lottery: Making All Tickets Winners,” arXiv:1911.11134 [cs, stat], Jul. 2021, Accessed: May 12, 2022. [Online]. Available: http://arxiv.org/abs/1911.11134

Relational Graphについて

• 論文の核となるコンセプト
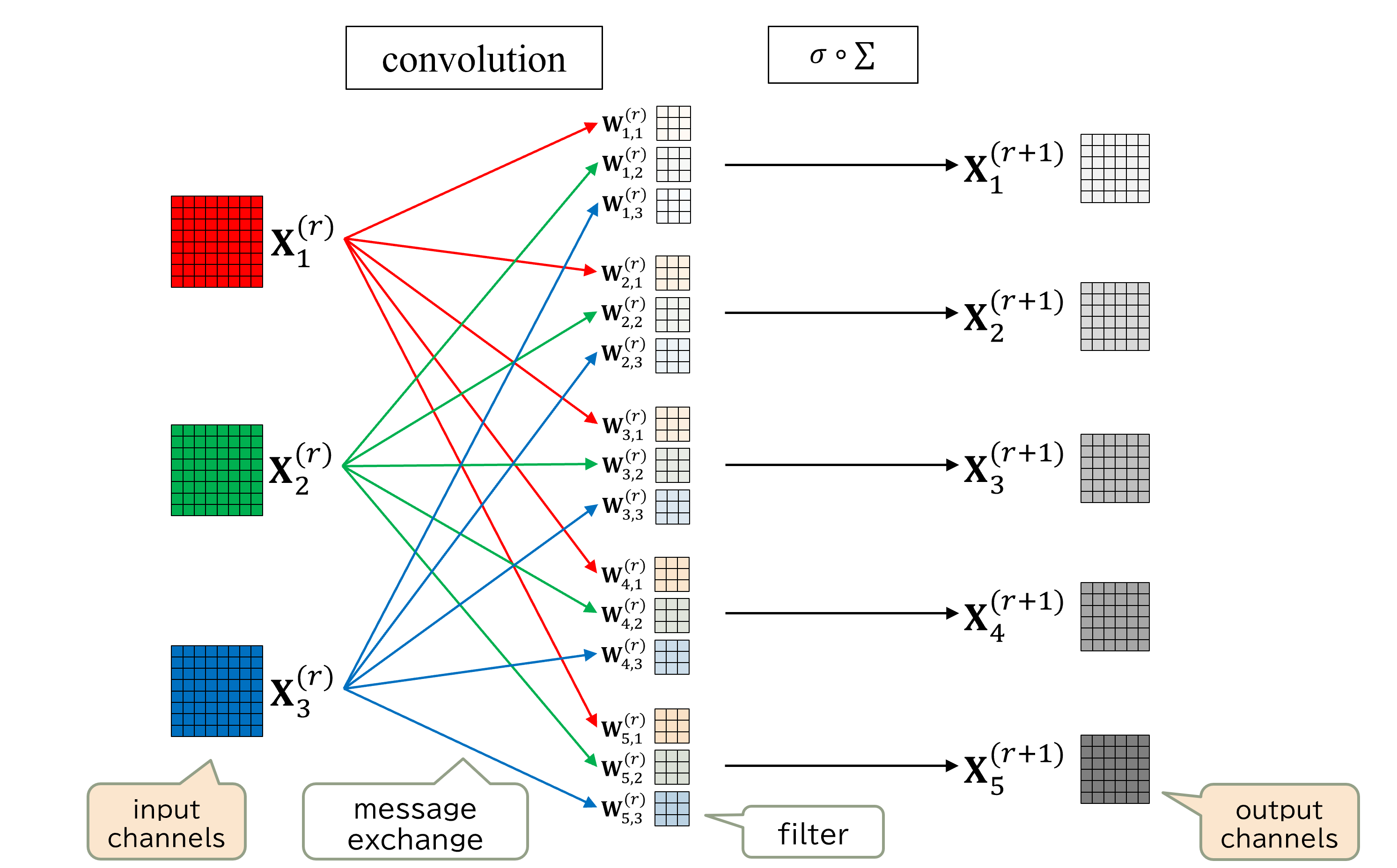
• 各畳み込みレイヤ内での、入出力チャネル間のメッセージ (値) の交換を表すグラフ

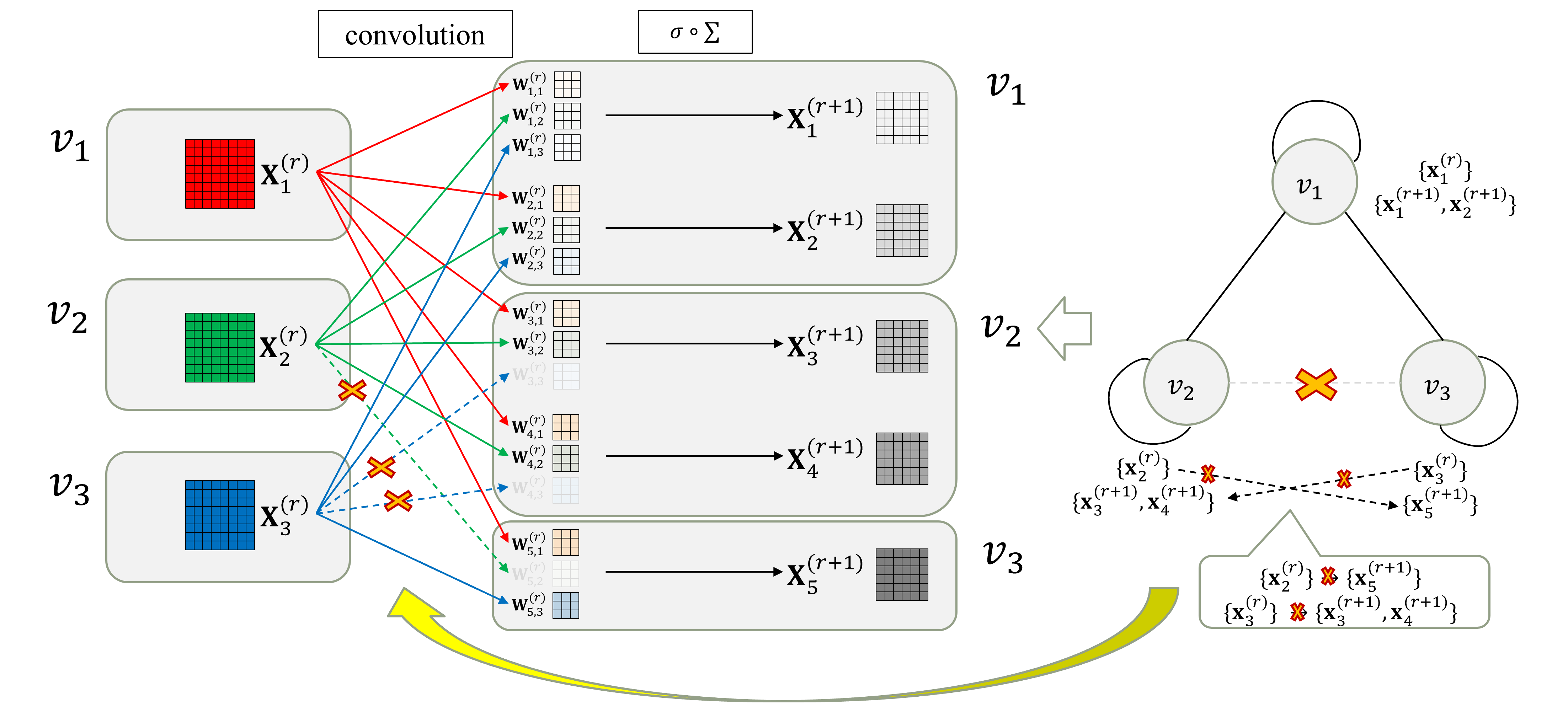
畳み込み層への適用例

• 図のような畳み込み層を考える

• 3ノードのRelational Graphへの変換例
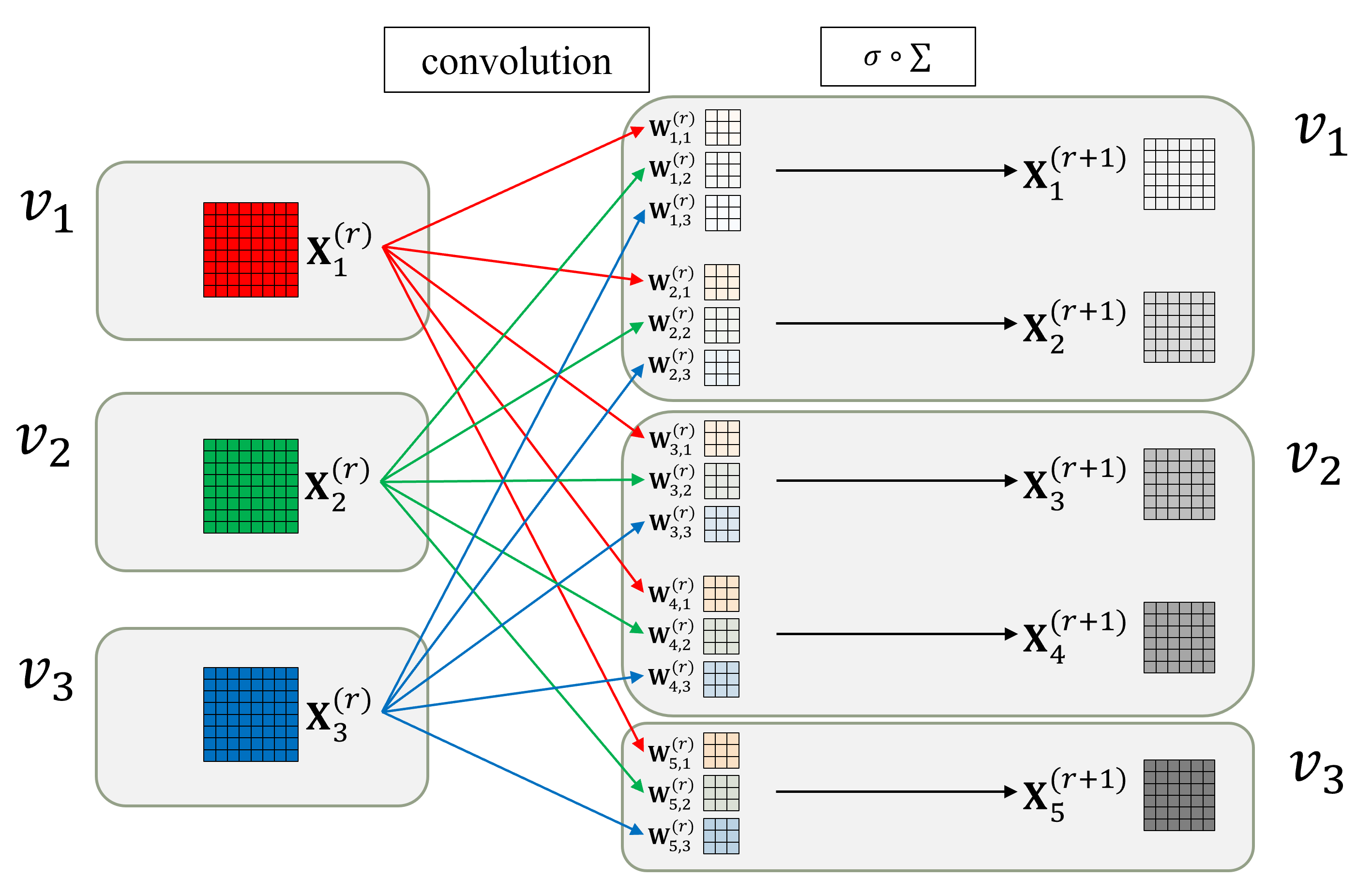
  • 入出力チャネルを、同じノード数 (3ノード) でグループ化

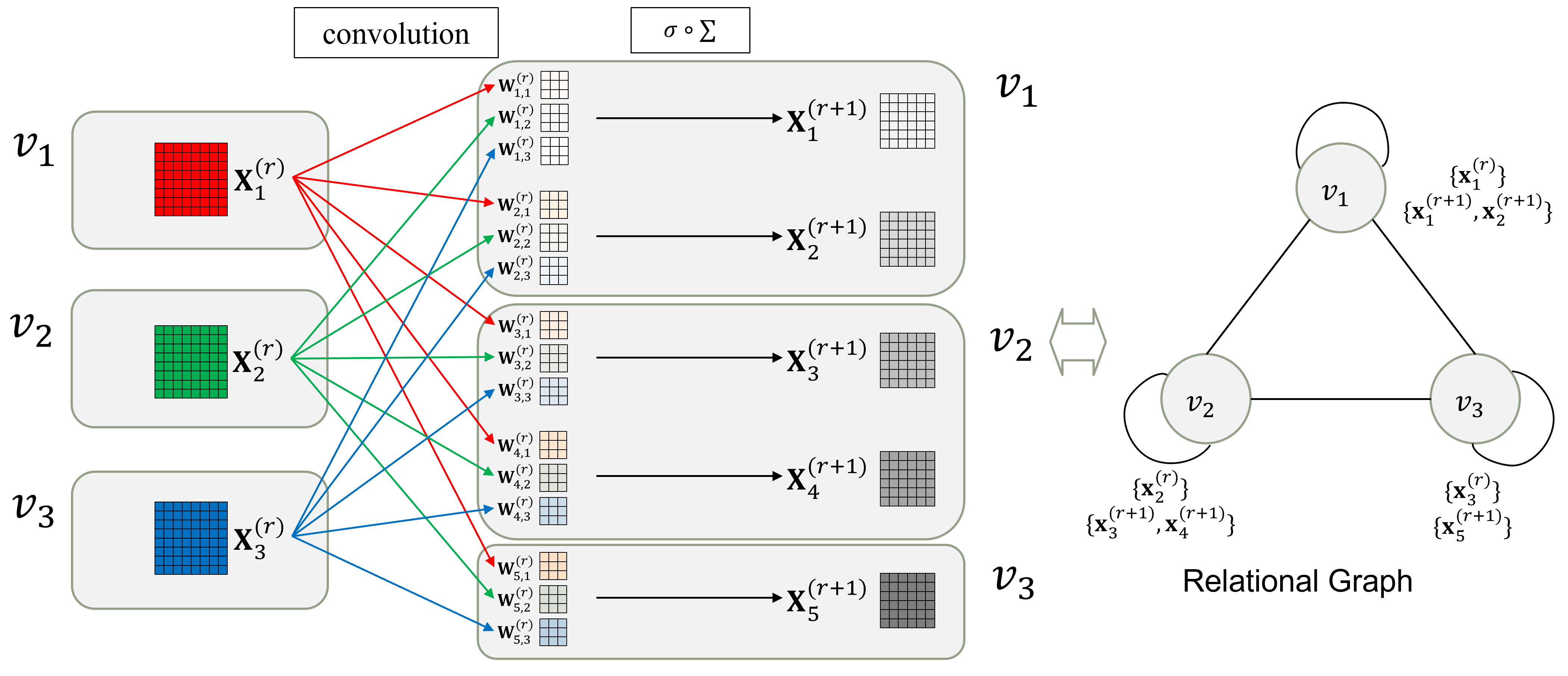
• 入出力間の値の交換を、Relational Graphにおけるノード間のエッジとしてモデル化
  • この論文ではself loopを含む無向グラフとしてモデル化
  • 全ての入出力チャネル間で値を交換⇒self loopを含む完全グラフに変換

• Relational Graphの変更例
  • ノード$v_2, v_3$ 間のエッジを削除
    ⇒ 対応する入出力チャネル間 ({$x_2^{(r)}$} $ \rightarrow $ {$x_5^{(r+1)}$}, {$x_3^{(r)}$} $ \rightarrow $ {$x_3^{(r+1)}, x_4^{(r+1)}$}) の値の交換を削除

提案のアプローチ

• 同一のRelational Graphを、ネットワーク全体の (最初と最後のレイヤ以外の) 全ての畳み込み層に同様に適用

• スパースなRelational Graphの適用時、(完全グラフを基にしたRelational Graphに対応する) BaselineとFLOPSを合わせるため、各ノードのwidth (チャネル数) を増やして調整
  • 『スパースな入出力チャネル間の接続 + チャネル数増加』の方が、Baselineの完全な入出力チャネル間の接続よりも精度が高い、というのが論文の主旨