特に名前のついていないテクニックが、名前がつくことで広く知れ渡って「典型」と化すことはよくあることと思います。競プロ界で俗に言う imos 法などはその代表例と言えます。桁 DP もその呼び名が固有名詞化したことで、smaller フラグを用いる考え方が普及したイメージです。
これに対して「部分文字列を走査する DP」のような名前のついていないテクニックは、なかなか典型と受け止められないイメージがあります。AUPC 2018 day3 北大セットの最終問題の解法も、この DP の考え方を知っていれば自然なものに思えます。本記事ではこの「部分列 DP」を特集してみます。誰かがいい名前を付けて固有名詞化してくれたらいいなと思いつつ...
0. はじめに --- 部分文字列とは
文字列 $S$ (例えば "nyanpasu") に対して、
- $S$ を構成する文字を $0$ 文字以上取り除き
- 残った文字を元の順番で並べる
ことによって得られる文字列を $S$ の部分文字列と呼びます。文字列 "nyanpasu" を例にとると
- 部分文字列の例 : "n", "ny", "yn" (2 文字目と 4 文字目), "nyau", "nyanpasu", ""
- 部分文字列ではない例: "x", "us", "pn", "nyanpasupasuun"
という感じです。特に「空文字列」や「元の文字列そのもの」も部分文字列です。
文字列 $S$ が与えられる。$S$ の部分文字列を数え上げよ。
というのは典型的な問題で、この問題に対する DP の考え方は、以下のような他の様々な問題にも応用が効きます:
注意
部分文字列と言った場合に、特に「連続する部分文字列」のことを指す場合もあるようです。これは特に、元の文字列から取り出す文字の index が連続しているものを指します。連続する部分文字列について扱うときは、本記事の部分文字列とは根本的に異なる手法をとることが多いです。
1. なにが難しいか
元の文字列 $S$ からの「文字の残し方」が異なっていても、同じ部分文字列を生成することがあります。例えば $S$ = "nyanpasu" について
- 1 文字目と 3 文字目と 7 文字目: "nas"
- 1 文字目と 6 文字目と 7 文字目: "nas"
- 4 文字目と 6 文字目と 7 文字目: "nas"
といった具合に異なる選び方で同じ "nas" が生成されます。これをダブルカウントすることなく数え上げる必要があります。
対策方法はとても簡単で、重複しないようなルールを決めてしまえばいいです。具体的には
同じ部分文字列を生成する選び方のうち、
選ぶ index の辞書順が最小になるものだけを考えて、それ以外は捨てる
という風にします。したがって上の例で言えば、
- (1, 3, 7) 文字目を選んだ "nas" は OK な部分文字列
- (1, 6, 7) 文字目を選んだ "nas" は NG な部分文字列 (なのでカウントしない、調べない)
- (4, 6, 7) 文字目を選んだ "nas" は NG な部分文字列 (なのでカウントしない、調べない)
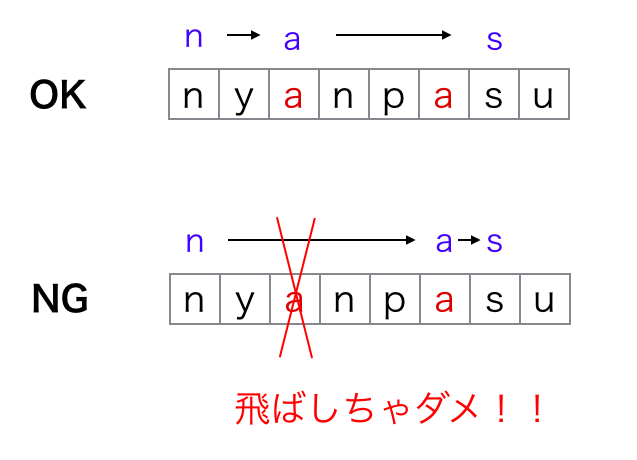
です。2 個目の (1, 6, 7) が NG になった原因ですが、"nyanpasu" の 1 文字目の 'n' を選んだ後に次の "a" を見つけたいのですが、直近 3 文字目に 'a' があるにもかかわらず飛ばして 6 文字目の 'a' を選んだのがダメだったということになります。
2. 部分列 DP
早速ですが、次のような問題を解いてみましょう!
問題 1: 部分文字列の数え上げ
【問題概要】
長さ $n$ の文字列 $S$ が与えられる。
$S$ の部分文字列 (空文字含む) として考えられるものの個数を数え上げよ。ただし答えがとても大きくなることがあるので、個数を 1,000,000,007 で割ったあまりを求めよ。
【制約】
- $1 \le n \le 10^{5}$
- $S$ に登場する文字は英小文字のみ (26 種類)
【数値例】
- $S$ = "abcde" のとき、32 通り (全文字が異なるので $2^5 = 32$ 通り)
- $S$ = "aaaaa" のとき、6 通り ("", "a", "aa", "aaa", "aaaa", "aaaaa")
- $S$ = "aba" のとき、7 通り ("", "a", "b", "aa", "ab", "ba", "aba")
部分列 DP テーブルの定義
さて、この問題でやりたいことの構造はナップサック問題と近いです。すなわち
- 各文字 (各アイテム) についてそれを「選ぶ」か「選ばない」の二択を繰り返して行く
という構造です。この種の構造をした問題に対してはしばしば DP が有効です。DP テーブルを以下のように定義します:
${\rm dp}[i]$ := 文字列 $S$ において、$i-1$ 番目の文字 (0-inedexed) は必ず使うものとして、$S$ のうち $0$ 番目から $i-1$ 番目までの部分から得られる部分文字列の個数
(ただし「同じ部分文字列を生成するなら選択 index が辞書順最小になるように」という上の章で述べたルールを守る)
ちょっと複雑ですが、例えば "nyanpasu" について
- ${\rm dp}[0] = 1$ ("" に対応します、文字列 $S$ の先頭に仮の文字列があるものとみなして、それのみを選ぶことに対応します)
- ${\rm dp}[1] = 1$ ("n" に対応します、"n" を選ばないといけないことに注意です)
- ${\rm dp}[2] = 2$ ("y" と "ny" に対応します)
- ...
という感じです。この DP テーブルが得られたら、最後の答えは
- $\sum_{i=0}^{n}$ ${\rm dp}[i]$
になります。これは $S$ の部分文字列のうち、最後に選び取る index で場合分けしていることになります。
部分列 DP の遷移式
${\rm dp}[i]$ が定義されているときに、遷移は「次に選ぶ文字を 'a' 〜 'z' で場合分け」して次のように考えます。次に選ぶ文字に応じて最左の index を選ぶことで、「同じ部分文字列を生成するなら辞書順最小な選び方をする」というルールを満たすことを保証しています。また、ここでは配る DP で書いています。
- 次の文字として 'a' を選ぶとき: $S$ の $i$ 文字目以降で最左の 'a' の index を $a$ として ${\rm dp}[a + 1]$ += ${\rm dp}[i]$
- 次の文字として 'b' を選ぶとき: $S$ の $i$ 文字目以降で最左の 'b' の index を $b$ として ${\rm dp}[b + 1]$ += ${\rm dp}[i]$
- ...
- 次の文字として 'z' を選ぶとき: $S$ の $i$ 文字目以降で最左の 'z' の index を $z$ として ${\rm dp}[z + 1]$ += ${\rm dp}[i]$
ここで、便利配列として
- ${\rm next}[i][c]$ := $S$ の $i$ 文字目以降で最初に文字 $c$ が登場する index
を前処理で求めておきます。これは以下のような関数で $O(n)$ でできます:
vector<vector<int> > calcNext(const string &S) {
int n = (int)S.size();
vector<vector<int> > res(n+1, vector<int>(26, n));
for (int i = n-1; i >= 0; --i) {
for (int j = 0; j < 26; ++j) res[i][j] = res[i+1][j];
res[i][S[i]-'a'] = i;
}
return res;
}
これを用いて以上の DP をまとめると
<DP 遷移式>
各文字 $c$ について、${\rm next}[i][c] < n$ ならば、${\rm dp}[{\rm next}[i][c] + 1]$ += ${\rm dp}[i]$
<DP 初期条件>
${\rm dp}[0] = 1$
<求める値>
$\sum_{i=0}^{n}; {\rm dp}[i]$
となります。C++ で実装すると以下のようになるでしょう。計算時間は $O(n)$ (より正確には $S$ に登場する文字の種類数を $K$ として $O(KN)$) になります。
# include <iostream>
# include <string>
# include <vector>
using namespace std;
const int MOD = 1000000007;
// res[i][c] := i 文字目以降で最初に文字 c が登場する index (存在しないときは n)
vector<vector<int> > calcNext(const string &S) {
int n = (int)S.size();
vector<vector<int> > res(n+1, vector<int>(26, n));
for (int i = n-1; i >= 0; --i) {
for (int j = 0; j < 26; ++j) res[i][j] = res[i+1][j];
res[i][S[i]-'a'] = i;
}
return res;
}
// mod 1000000007 の世界で a += b する関数
void add(long long &a, long long b) {
a += b;
if (a >= MOD) a -= MOD;
}
int main() {
// 入力
string S; cin >> S;
int n = (int)S.size();
// 前処理配列
vector<vector<int> > next = calcNext(S);
// DP
vector<long long> dp(n+1, 0);
dp[0] = 1; // 初期化、空文字列 "" に対応
for (int i = 0; i < n; ++i) {
for (int j = 0; j < 26; ++j) {
if (next[i][j] >= n) continue; // 次の文字 j がもうない場合はスルー
add(dp[next[i][j] + 1], dp[i]);
}
}
// 集計
long long res = 0;
for (int i = 0; i <= n; ++i) add(res, dp[i]);
cout << res << endl;
}
3. 問題例
似た考え方をする問題をいくつか見てみます。
問題 2: AOJ 2895 回文部分列 (AUPC 2018 day3 G)
【問題概要】
文字列 $S$ が与えられる。$S$ の部分文字列のうち回文となっているものが何通りあるか、$1000000007$ で割ったあまりで求めよ。
【制約】
- $1 \le |S| \le 2000$
- $S$ は英小文字のみからなる
【解法】
部分文字列のうち、特に回文になっているものを数え上げる問題です!
単純な部分文字列の数え上げ問題では「同じ部分文字列を生成するような index の選び方のうち、辞書順が最小になるものだけを考えて左寄せする」という感じでやっていましたが、それと同様にして
- 同じ回文部分文字列を生成する選び方のうち、両端になるべく寄せる
という風にやればよいです。ここでは簡単のため、$S$ を反転した文字列を $T$ として、$S$ と $T$ をそれぞれ左から見ていって、同じ文字になっているところを抜き出して行く問題だと思うことにします。例によって
- ${\rm ns}[i][c]$ := $S$ の $i$ 文字目以降で最初に文字 $c$ が登場する index (存在しないときは $n$)
- ${\rm nt}[i][c]$ := $T$ の $i$ 文字目以降で最初に文字 $c$ が登場する index (存在しないときは $n$)
という配列を前処理して用意しておきます。そして $S$ と $T$ とで共通する文字を取って行くイメージの DP を立てます:
- ${\rm dp}[i][j]$ := $S$ の $0$ 文字目から $i-1$ 文字目までと、$T$ の $0$ 文字目から $j-1$ 文字目までとを使ってできる回文の個数 ($S$ の $i-1$ 番目の文字と、$T$ の $j-1$ 番目の文字は必ず採用するものとします)
として、各アルファベット $c$ に対して
${\rm dp}[ {\rm ns}[i][c] + 1 ][ {\rm nt}[j][c] + 1 ]$ += ${\rm dp}[ i ][ j ]$
という感じの遷移をすれば OK です。そして最後の集計では、$i + j <= n$ を満たす $i$, $j$ に対して、
- ${\rm dp}[i][j]$ に「(元の文字列 $S$ の左側 $i$ 文字分と右側 $j$ 文字分を削り取って残る文字列中に含まれる文字の種類数) $+ 1$」を掛け算したもの
を合算していけばよいです。これは奇数長の回文を作るときに真ん中の文字となりうる文字の個数を調べています。「$+ 1$」は偶数長の回文に対応しています。
# include <iostream>
# include <string>
# include <vector>
# include <algorithm>
# include <set>
using namespace std;
const int MOD = 1000000007;
// res[i][c] := i 文字目以降で最初に文字 c が登場する index (存在しないときは n)
vector<vector<int> > calcNext(const string &S) {
int n = (int)S.size();
vector<vector<int> > res(n + 1, vector<int>(26, n));
for (int i = n - 1; i >= 0; --i) {
for (int j = 0; j < 26; ++j) res[i][j] = res[i + 1][j];
res[i][S[i] - 'a'] = i;
}
return res;
}
void add(long long &a, long long b) {
a += b;
if (a >= MOD) a -= MOD;
}
int main() {
string S; cin >> S;
int n = (int)S.size();
string T = S;
reverse(T.begin(), T.end());
auto ns = calcNext(S);
auto nt = calcNext(T);
vector<vector<long long> > dp(n + 1, vector<long long>(n + 1, 0));
dp[0][0] = 1;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 26; ++k) {
int ni = ns[i][k];
int nj = nt[j][k];
if (ni + nj + 2 > n) continue;
add(dp[ni + 1][nj + 1], dp[i][j]);
}
}
}
long long res = 0;
for (int i = 0; i <= n; ++i) {
for (int j = 0; i + j <= n; ++j) {
int num = 1;
for (int k = 0; k < 26; ++k) if (ns[i][k] + 1 + j <= n) ++num;
res = (res + dp[i][j] * num % MOD) % MOD;
}
}
cout << res - 1 << endl;
}
問題 3: ARC 081 E - Don't Be a Subsequence
【問題概要】
文字列 $A$ が与えられる。
$A$ の部分文字列とはならないような文字列 (英小文字のみ) のうち、最短の長さのものを求めよ。複数考えられる場合にはそのうち辞書順最小のものを求めよ。
【制約】
- $1 \le |A| \le 2 × 10^5$
- $A$ は英小文字のみからなる
【解法】
今回は「辞書順最小な復元をする」という要求もあります。そのような復元を要求する場合には
- 後ろから DP する
というのが典型対策と言えるでしょう。これまで見て来た部分列 DP に対して「後ろから DP」という形に対応して、以下のようにします。ここで、${\rm next}[i][c]$ 配列は上と同様、$S$ の $i$ 文字目以降で最初に文字 $c$ が登場する index です。
なお、これまで見て来た部分列 DP は DP テーブルの定義に「$i$ 文字目は必ず使うものとして」といった制約が入っていることが多かったですが、後ろから遷移していく形にすると、この種の制約を外せるケースが多いようです。
【DP 定義】
${\rm dp}[i]$ := $i$ 文字目以降について「部分文字列とならない」最短の文字列長
(今までの通常の「部分文字列数え上げ DP」と異なり、必ずしも $i$ 文字目自体を採用しなくてもよいです)
【DP 遷移】
${\rm dp}[i]$ = $\min_{c} ({\rm dp}[{\rm next}[i][c]+1] + 1)$
(${\rm i}$ 文字目以降について最初に選ぶべき文字の種類を 'a'〜'z' で場合分けしています)
【DP 初期化】
${\rm dp}[n] = 1$
# include <iostream>
# include <string>
# include <vector>
using namespace std;
// chmin
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }
// res[i][c] := i 文字目以降で最初に文字 c が登場する index (存在しないときは n)
vector<vector<int> > calcNext(const string &S) {
int n = (int)S.size();
vector<vector<int> > res(n+2, vector<int>(26, n+1));
for (int i = n-1; i >= 0; --i) {
for (int j = 0; j < 26; ++j) res[i][j] = res[i+1][j];
res[i][S[i]-'a'] = i;
}
return res;
}
string solve(const string &S) {
int n = (int)S.size();
// 前処理配列
auto next = calcNext(S);
// DP
vector<int> dp(n+1, 1<<29); // DP テーブル
vector<char> recon(n+1, 'a'); // 復元用テーブル
dp[n] = 1;
for (int i = n - 1; i >= 0; --i) {
for (int j = 0; j < 26; ++j) {
// 次の文字がないとき
if (next[i][j] == n+1) {
if (dp[i] > 1) {
dp[i] = 1;
recon[i] = 'a'+j;
}
}
// 次の文字があるとき
else if (chmin(dp[i], dp[next[i][j] + 1] + 1)) {
recon[i] = 'a'+j;
}
}
}
// 復元
string res = "";
int index = 0;
while (index <= n) {
res += recon[index];
index = next[index][recon[index]-'a'] + 1;
}
return res;
}
int main() {
string S;
cin >> S;
cout << solve(S) << endl;
}
問題 4: Typical DP Contest G - 辞書順
【問題概要】
文字列 $S$ が与えられる。
$S$ の部分文字列のうち、辞書順で $K$ 番目のものを求めよ。
(ただし空文字列は部分文字列に含めない)
【制約】
- $1 \le |S| \le 10^6$
- $S$ は英小文字のみからなる
- $1 \le K \le 10^{18}$
【解法】
とりあえず辞書順に関する復元を要求されているので、前問と同様「後ろから DP」をします。少し考えてみると
- ${\rm dp}[i][c]$ := $i$ 文字目以降について文字 $c$ から始まる部分文字列の個数
という風にすると良さそうです。このようにしておくと部分文字列の数え上げができるだけでなく、辞書順 $K$ 番目の部分文字列が何であるかの決定までできます!!!
例えば先頭の文字を決定したいと思ったら、
- ${\rm dp}[0][$'${\rm a}$'$] \le K$ ならば、先頭の文字は '${\rm a}$'
- それ以外で ${\rm dp}[0][$'${\rm b}$'$] \le K - {\rm dp}[0][$'${\rm a}$'$]$ ならば、先頭の文字は '${\rm b}$'
- それ以外で ${\rm dp}[0][$'${\rm c}$'$] \le K - {\rm dp}[0][$'${\rm a}$'$] - {\rm dp}[0][$'${\rm b}$'$]$ ならば、先頭の文字は '${\rm c}$'
- ...
という風にして、先頭の文字を決定することができます。先頭の文字が例えば 'c' だとわかったならば、
- $K = K - {\rm dp}[0][$'${\rm a}$'$] - {\rm dp}[0][$'${\rm b}$'$] - 1$ として
- 同様のことを ${\rm dp}[1][$'${\rm a}$'$]$, ${\rm dp}[1][$'${\rm b}$'$]$, ... について実行する
ことによって二番目の文字を決定することができます。$K = K - {\rm dp}[0][$'${\rm a}$'$] - {\rm dp}[0][$'${\rm b}$'$] - 1$ の「$-1$」の部分についてですが、部分文字列として '${\rm c}$' で終わって残りは何も使わないものがあるので、その分を引いています。以後これを繰り返すことで、辞書順 $K$ 番目の部分文字列を復元できることがわかりました!
残りの課題は上記の ${\rm dp}$ テーブルの求め方ですが、上記のように定義していると実は ${\rm next}$ 配列が必要ないことがわかります。以下のような遷移で求められます。
- 各文字 $c$ に対して、
- $S[i]$ != $c$ ならば ${\rm dp}[i][c]$ += ${\rm dp}[i+1][c]$
- $S[i]$ == $c$ ならば ${\rm dp}[i][c]$ += $\sum_{c_2}{\rm dp}[i+1][c_2] + 1$
- 「最左採用ルール」によって、$S$ の ${\rm i}$ 文字目が ${\rm c}$ なら、それは必ず使います
- そしてその次の文字 $c_2$ を場合分けします
- $c$ を採用した後残りは採用しないケースもあるので、$+ 1$ します
# include <iostream>
# include <string>
# include <vector>
using namespace std;
long long INF = 1LL<<60;
void add(long long &a, long long b) { a += b; if (a >= INF) a = INF; }
int main() {
string S; long long K;
cin >> S >> K;
int n = (int)S.size();
// DP
vector<vector<long long> > dp(n+1, vector<long long>(26, 0));
dp[n-1][S[n-1] - 'a'] = 1;
for (int i = n-2; i >= 0; --i) {
for (int c = 0; c < 26; ++c) {
if (c != (int)(S[i] - 'a')) {
add(dp[i][c], dp[i+1][c]);
}
else {
add(dp[i][c], 1); // c を採用した後は何も採用しないケース
for (int c2 = 0; c2 < 26; ++c2)
add(dp[i][c], dp[i+1][c2]);
}
}
}
// 復元
long long sum = 0;
for (int c = 0; c < 26; ++c) add(sum, dp[0][c]);
// 部分文字列の個数が K に満たない場合
if (sum < K) {
cout << "Eel" << endl;
}
else {
string res = "" ;
for (int i = 0; i < n; ++i) {
// 次の文字が何かを決める
int j;
for (j = 0; j < 26; ++j) {
if (K - dp[i][j] <= 0) break;
K -= dp[i][j];
}
char c = 'a' + j; // 次の文字は c
res += c;
--K; // c をとって終了し、残りは何も取らないような文字列を除外
if (K <= 0) break; // K <= 0 になるなら c で終了
while (S[i] != c) ++i;
}
cout << res << endl;
}
}
4. その他の問題
部分列 DP の考え方で解ける問題を見つけたら、ドンドン記載して行きます:
- CS Academy 057 D - Distinct Palindromes (「AOJ 2895 回文部分列」と全く同じです)
- AOJ 1392 Shortest Common Non-Subsequence (ICPC Asia 2018 D) (ARC 081 E - Don't Be a Subsequence の文字列 2 個バージョンですね)
- SRM 435 DIV1 Medium DNADeletion (最左のものをとっていく考え方を適用します)
- AGC 027 E - ABBreviate (最後の最後で部分列 DP みたいな考え方の DP をします)
- square869120Contest #5 H - Percepts of Atcoder (TDPC G からさらに考察を積み重ねます)