本記事では、かの有名なResNetが提案された論文「Deep Residual Learning for Image Recognition」 (CVPR 2016) [1]を紹介します。また、論文中で取り組まれているCIFAR-10 classificationのコードを実装し (GitHub) 、実際に再現実験を行ってみました。
この論文で提案されているResNetは、ImageNetの分類精度を競うコンペであるILSVRCで優勝しただけでなく、深いネットワークを扱う提案手法の有効性と汎用性から、極めて多様なタスクで活用されています(引用数は2020年8月現在で52000を超えています)。
論文解説
概要
深いニューラルネットワークはこれまで学習することが難しいと言われていました。この論文では、真値を直接学習するのではなく、「残差」(真値との差分)を学習するニューラルネットワークのブロックを多数連結した構造を用いることで、深いネットワークの学習を容易にし、様々な画像認識タスクにおいて性能が大きく向上しました。
背景
画像認識では、ネットワークの階層が深くなるほど、より「深い」意味的特徴を抽出できることが知られています。しかし、単純にネットワークの階層を重ねていくだけでは勾配消失/勾配爆発といった問題が生じ、ネットワークのパラメータが収束せず学習がうまく行えませんでした。
この収束が困難であるという問題はネットワークの初期値や、正規化の手法により解決が図られてきましたが、たとえ収束しても、層を深くすると精度が下がるという問題が存在しました(これは過学習ではなく、下のグラフのようにtraining errorも悪くなります)。
(図は論文より。以下も同じ)
提案手法
この論文で提案されている手法は、小さな"residual block"を、多数接続することで階層の深いネットワークを実現するという手法です。一つ一つのresidual blockは、以下の図のように複数のweight layerとidentity mappingからなっています。このblock全体に表現させたい関数が $ H(x) $ だとしたとき、weight layerが組み合わさった部分では $ F(x) = H(x) - x $ を学習することになります。これが"residual"(残差)と呼ばれる所以です。
この手法は、背景の最後で述べた「層が深くなると精度が下がる」という問題の解決につながります。実は複数層の非線形層は、identity mapping( $ H(x) = x $ )の学習が難しく、層を増やしたときにidentity mappingが最適解であるようなブロックにおいてこのmappingがうまく学習できず、精度が落ちると言われています。
しかし、提案したresidual blockを用いれば、単にweight layerの重みを0にするだけで容易にidentity mappingを学習することができます。実用上は真にidentityであることはまれですが、 $x$ と $H(x)$ が非常に小さいようなケースでの学習を容易にできます。
Residual blockの詳細
Residual blockの出力を$y$としたとき、blockはこのような演算で表せます。
$$y = F(x) + x$$
この$F(x)$は、2層以上のレイヤを組み合わせて実現されます。例えば、上に載せた図ではレイヤが2層であるため、$\sigma$をReLU関数として
$$F(x) = W_2\sigma(W_1x)$$
のように表せます(ここではバイアス項は省略しています)。ReLUによる非線形演算は、最後の加算のあとにも行われるため、実際は
$$y = \sigma(W_2\sigma(W_1x) + x)$$
のようになります。なお、$x$と$F(x)$のチャネル数が合わない場合は、0埋めを行うか、1x1 convolutionを行うことでチャネル数を合わせています。
全体のネットワーク構造
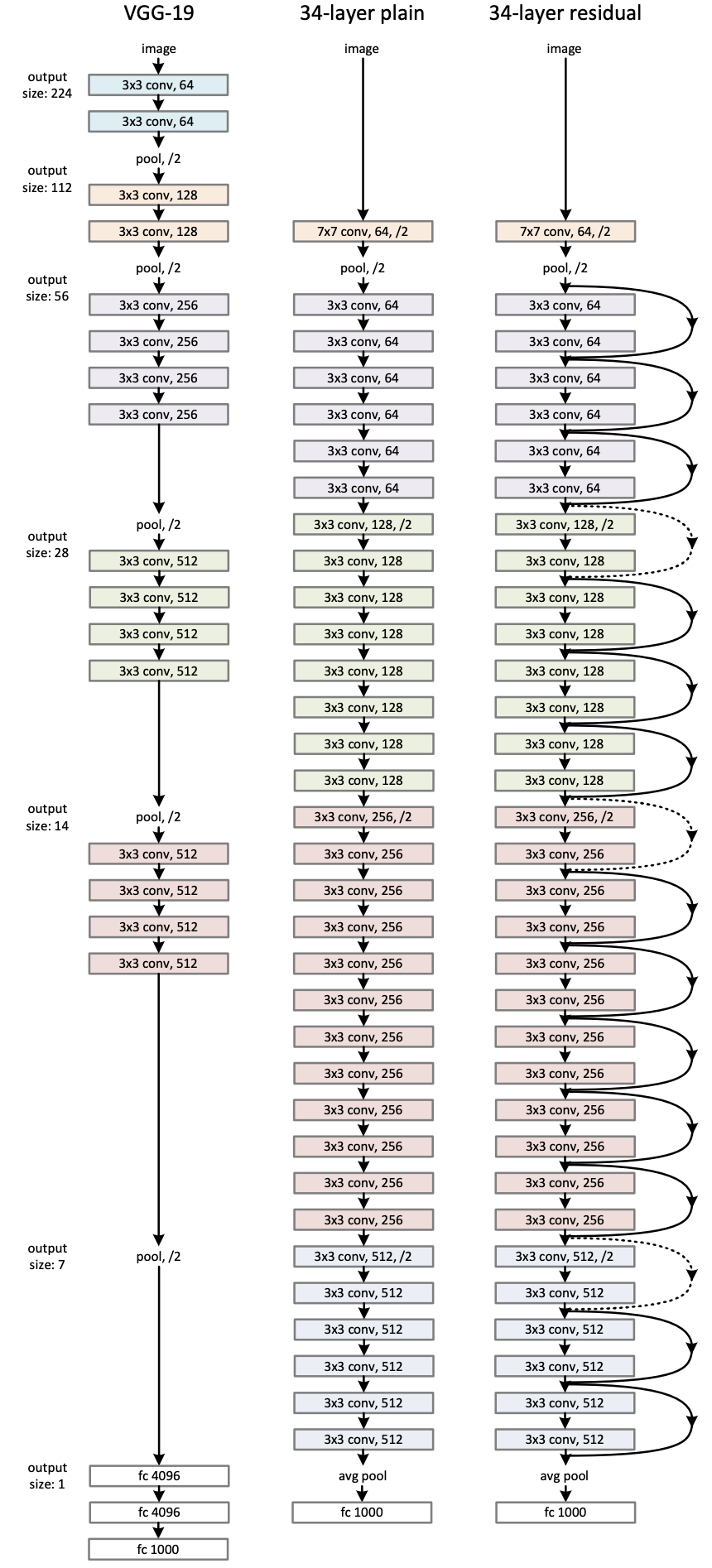このネットワーク図は、ImageNetの分類問題を解くためのネットワークです。一番右の図が提案手法です。
特徴マップの大きさが同じであればチャネル数も同じ、特徴マップの大きさを半分にしたらチャネル数を倍にする、という原則のもとネットワーク構造を設計しています。特徴マップの大きさを小さくする操作は基本的に1層目のconvolutionのstrideを2にする、という操作で行い、poolingは(最初と最後以外)行っていません。(ちなみに最後のFC層に入れる前のpoolingはGloval Average Poolingです。)
Batch Normalizationは、各convolutionの直後に実行されます。
データセットごとの実装の違い
※ 仔細なハイパーパラメータ類に関してはここでは省略します。
ImageNet
ImageNetの画像分類では、以下の表のネットワークが用いられています。50層以上のネットワークでは、residual blockの構造が少し変化しており、これを"bottleneck architecture"と呼んでいます。これまで2層で構成されていた$F(x)$を3層とし、1層目と2層目は浅いチャネル数で構成するというのが特徴となっています。なお、これは計算コストを意識した改変で、精度はあまり変わらないと述べられています。実際152層のネットワークでも、VGG-16/19より計算量が少なくなっています。
チャネル数が異なるときのidentity mappingの加算は、チャネル数が異なる場合のみ 1x1 convolutionを行うという手法を採用しています。
CIFAR-10
CIFAR-10の画像分類は、入力の画像サイズがImageNetよりかなり小さいため、ネットワーク構造も少し変化しています。最初の層は単一の3x3 convolutionで、それ以降はresidual blockが続いていきます。convolution層は$6n+1$個の層が用いられ、以下の表のような内訳となります。結果的に、$3n$個のresidual blockができます。
この$6n+1$個の層の後にGloval Average Poolingが行われ、10層のFC層を用いて分類が行われます。$n = \{ 3, 5, 7, 9\}$で実験が行われ、それぞれ$20, 32, 44, 56$層のネットワークとなります。
チャネル数が異なるときのidentity mappingの加算は、不足する部分を0埋めするという手法がとられています。
再現実装
本論文で取り上げられたデータセットのうち、CIFAR-10の分類問題を解くコードをPyTorchを用いてすべて実装しました。
ソースコードの全体はGitHubに掲載しました。
コード
特に重要なモデル定義の部分のみ、こちらにも掲載します。Residual blockを1つのクラスResNetCifarBlockとして実装し、同じチャネル数のグループを作る汎用的な関数make_resblock_groupを実装することで簡潔で拡張性のあるコードとなるようにしています。特徴マップのサイズとチャネル数が変わるところでは、まずピクセルの間引きを行い、次いで0埋めを行っています。
import torch
import torch.nn as nn
import torch.nn.functional as F
class ResNetCifarBlock(nn.Module):
def __init__(self, input_nc, output_nc):
super().__init__()
stride = 1
self.expand = False
if input_nc != output_nc:
assert input_nc * 2 == output_nc, 'output_nc must be input_nc * 2'
stride = 2
self.expand = True
self.conv1 = nn.Conv2d(input_nc, output_nc, kernel_size=3, stride=stride, padding=1)
self.bn1 = nn.BatchNorm2d(output_nc)
self.conv2 = nn.Conv2d(output_nc, output_nc, kernel_size=3, stride=1, padding=1)
self.bn2 = nn.BatchNorm2d(output_nc)
def forward(self, x):
xx = F.relu(self.bn1(self.conv1(x)), inplace=True)
y = self.bn2(self.conv2(xx))
if self.expand:
x = F.interpolate(x, scale_factor=0.5, mode='nearest') # subsampling
zero = torch.zeros_like(x)
x = torch.cat([x, zero], dim=1) # option A in the original paper
h = F.relu(y + x, inplace=True)
return h
def make_resblock_group(cls, input_nc, output_nc, n):
blocks = []
blocks.append(cls(input_nc, output_nc))
for _ in range(1, n):
blocks.append(cls(output_nc, output_nc))
return nn.Sequential(*blocks)
class ResNetCifar(nn.Module):
def __init__(self, n):
super().__init__()
self.conv = nn.Conv2d(3, 16, kernel_size=3, stride=1, padding=1)
self.bn = nn.BatchNorm2d(16)
self.block1 = make_resblock_group(ResNetCifarBlock, 16, 16, n)
self.block2 = make_resblock_group(ResNetCifarBlock, 16, 32, n)
self.block3 = make_resblock_group(ResNetCifarBlock, 32, 64, n)
self.pool = nn.AdaptiveAvgPool2d(output_size=(1, 1)) # global average pooling
self.fc = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.bn(self.conv(x)), inplace=True)
x = self.block1(x)
x = self.block2(x)
x = self.block3(x)
x = self.pool(x)
x = x.view(x.shape[0], -1)
x = self.fc(x)
return x
使用したデータセットと各種パラメータ
論文に記載されているものは、全てそれに従っています。
データセット
CIFAR-10は10クラス・6万枚の画像を含むデータセットで、この5万枚を訓練用、1万枚を評価用として用いました。画像サイズは32x32です。
パラメータ
- Batch size: 128
- Iterations: 64k
- Optimizer: SGD + momentum (0.9) + weight decay (0.0001)
- Learning rate: 0.1で開始し、32k/48kイテレーションでそれぞれ1/10倍
- Initialization: Heの初期値
- 訓練時のdata augmentation:
- 各辺に4ピクセルの0-paddingを行い、32x32でランダムクロップ
- 水平方向の反転
結果
上記の設定で学習をそれぞれ行い、評価した結果が以下です。評価の指標としてはTop-1のerror rateを用いています。5回の実行での平均 ± 標準偏差を表しています。
| 手法 | $n$ | Top-1 error rate (%) | Reported error rate (%) |
|---|---|---|---|
| ResNet-20 | 3 | 8.586 ± 0.120 | 8.75 |
| ResNet-32 | 5 | 7.728 ± 0.318 | 7.51 |
| ResNet-44 | 7 | 7.540 ± 0.475 | 7.17 |
| ResNet-56 | 9 | 7.884 ± 0.523 | 6.97 |
層が深くなるほどエラー率のばらつきが大きくなっていき、平均値が論文で報告された値とは離れていっていますが、概ね論文値に近い値が出ているといえます。(書いてはありませんでしたが、論文値が複数回実行してbestを用いているということならば妥当な値とも思います。)
参考文献
- [1] He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.