特にネタが思いつかなかったため、昔せっせと自分でエンコーダを作っていたjpgの内部構造について記事をしたためたいと思います_(:3」∠)_
※注意 このお話で紹介するのはjpgの
1フォーマットに過ぎません。
全てのjpgがこのアルゴリズムで
動いてはいませんので悪しからず… (jpg2000, 可逆jpg, etc…)
そもそもjpgとは?
- 静止画像を圧縮する方式の1つ
- 非可逆圧縮
- デジカメなんかの記録方式もコレ(exifとか特殊なヘッダがくっついている)
- 画像の品質が低いとブロックノイズ発生
なんてお話を切り出してみたものの、とても1回では書ききれないため、今回はjpgの圧縮に用いられている主要なアルゴリズムについて触れていきたいと思います。
今回説明する主要アルゴリズムは以下の3つ
主要アルゴリズム
- ランレングス(ゼロランレングス)
- ハフマン符号
- 2次元DCT
順にどのようなアルゴリズムなのか説明していきます。
ランレングス
ある連続したデータを、そのデータ1つ分と連続した長さで表現すること
例
AAAAABBBBBBBBBAAA
↓
A5B9A3
- 可逆圧縮
- 0(数字のゼロ)に対して行う場合を特別にゼロランレングスという
- 連続したデータが多ければ多いほど高圧縮
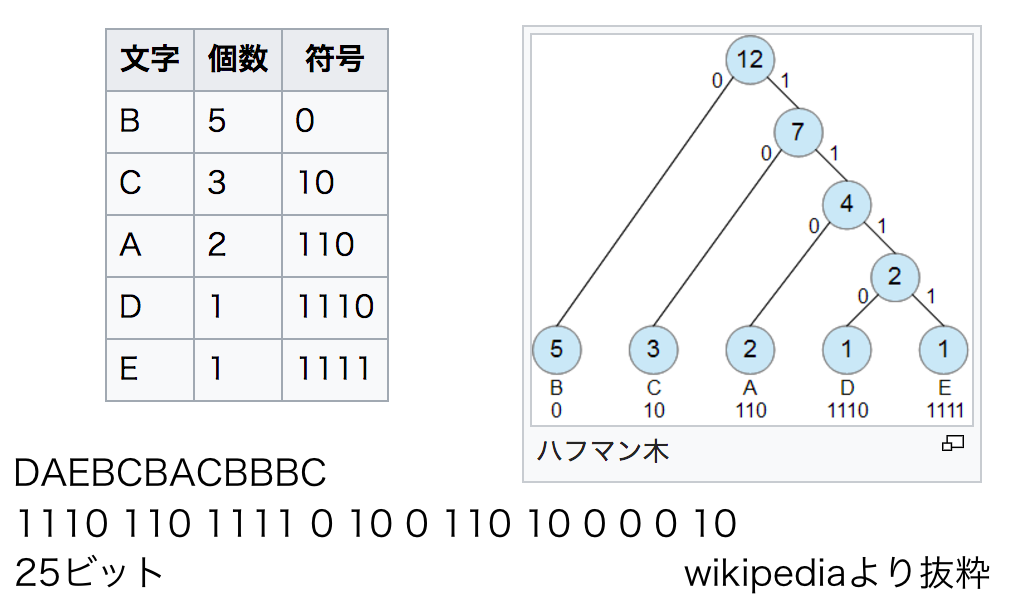
ハフマン符号
よく出現する文字には短いビット列、 あまり出現しない文字には長いビット列 を割り当てることで総データ量の 削減を狙うエントロピー符号
- 可逆圧縮
- 接頭符号(先頭から順に判定していって、必ず一意に符号化できるもののこと)
- ハフマン木より生成
例
2次元DCT
DCTを2次元空間に適用したもの
そもそもDCT(discrete cosine transform)とは
- 離散コサイン変換
- 離散信号を周波数領域へ変換する1つの方法
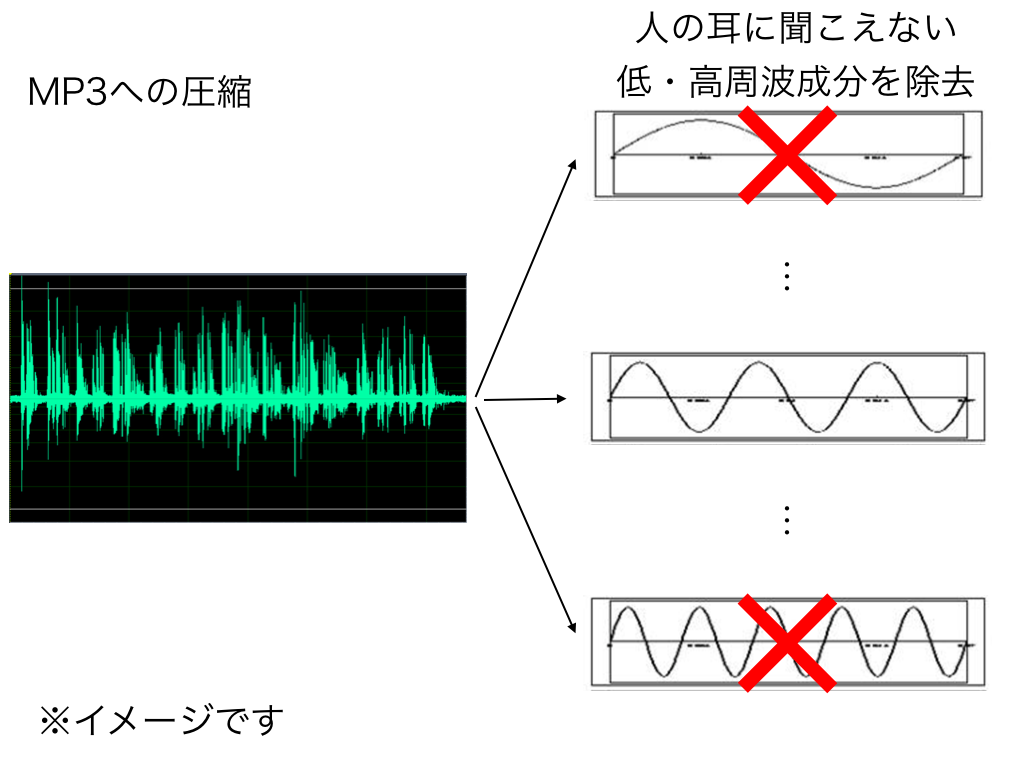
- MP3などの圧縮に利用されている
MP3 → 1次元DCT
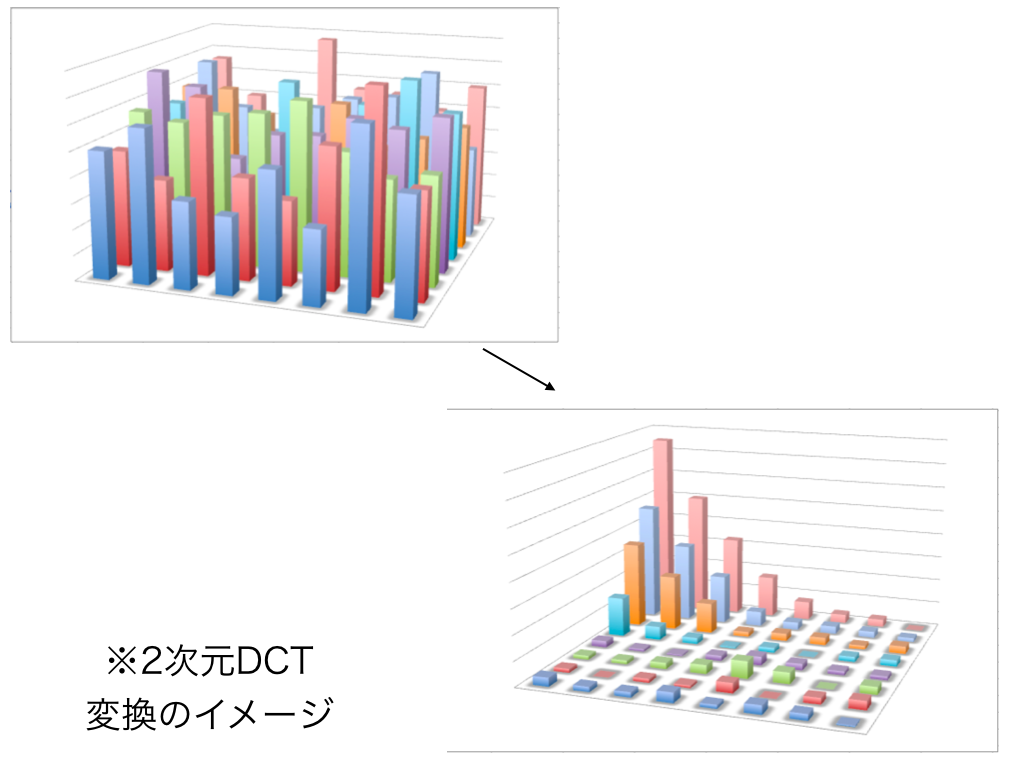
画素平面の2次元に適用したもの → 2次元DCT
音の周波数領域はイメージしやすいが、はて、画素の周波数領域? …それってなんぞ?
ここはイメージしづらいところですが、離散データを特定の成分ごとに分離する手法と捉えてください。
(逆の変換をかければ元の離散データに復元可能)
今回はここまで(๑•̀ㅂ•́)و✧
上記で挙げたアルゴリズムの他にも高い圧縮率を出すための工夫として
- YCbCr変換
- ジクザクスキャン
- DC成分AC成分
- 4:1:1
など様々な先人の知恵が盛り込まれています。
次回は上記含めて実際の処理フローについて見ていきたいと思います。
つづく