はじめに
全国 8,120 万人のレイトレファン の皆様こんにちは!
WebGL でレイトレがどうしてもやりたいんだというお便りがついに 1,021 万通を超えたので、そろそろ WebGL で簡単なレイトレーシングの実装について解説する頃合いかなと思い立ち筆を執った次第です。
今回はあくまでも 基本に忠実 に、簡単なレイトレーシングの実装を GLSL だけで行ってみましょう。全国のレイトレファンの皆さんの声援に応えてがんばって解説記事を書いていこうと思います。
前置き
私は幸運なことに WebGL について解説する機会がそれなりにあります。
そういった席ではよく、数学的な知識はとりあえず後回しにしてまずはやってみることからスタートしましょうという話をします。たとえば行列やクォータニオンについて、その数学的な詳細にまで勉強するのは大変です。ですから、まずは使い方から覚えようという促し方をするわけですね。
しかし、残念ながらレイトレの場合は数学的なことを無視しながら修得するのはちょっと難しいですね。
例えば、ベクトルや内積や外積といったレベルの、ある程度の数学の知識がない状態でレイトレに取り組もうとしても、コードをコピーするところまでが精一杯。自分なりの修正を加えることは難しいと思います。
ただ、基本を習得してからでないとレイトレに触れてはいけないかというと、そんなことはないのです。少しでも興味を持ったのなら、まずはこのテキストを最後までがんばって読んでみましょう。最後まで読み切ることができたのなら、きっとあなたは立派なレイトレ戦士になれる素質がありますよ!
まずは 興味をもつこと 、そして一度に理解できなくても何度もいろんな文献を漁ったりコードを読んだりすること。これが大事なのではないかなと思います。
実行環境
WebGL と GLSL を用いてコーディングを行いますので、必要となるのは WebGL が実行できるハードウェアとブラウザのみです。
私が作った GLSL オンラインエディタ がありますので、テキストエディタを個別に用意する必要さえありません。もちろん、ローカルでお好きなエディタを用いてコーディングして、実行だけオンラインエディタを使ったっていいでしょう。
とにかく気軽に始められますから、変に気負いせず、気持ち軽やかにやっていきましょう。
また、今回は GLSL に関しては一応最低限の知識がある前提で書きます。GLSL の基本から解説し始めてしまうととんでもない文章量になってしまうので、そのあたりはご了承ください。
ちなみに手前味噌で恐縮ですが、GLSL によるシェーダコーディングの基本は以下のリンクなど参考になさるとよろしいかと思います。全十回にわたって連載形式で解説しています。
[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(1) - Qiita
とりあえずレイを飛ばしてみっか!
なにはなくとも、レイトレーシングというくらいですから、まずはレイを飛ばさないことには始まりませんね。サクッとレイを飛ばすためのコードを書いてみましょう。
// r は resolution、つまりスクリーンサイズ
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
まず上記のコードを見てください。
このシェーダには、 uniform 変数(外部からシェーダに送られてくるデータが入っている変数)として resolution、つまりスクリーンの解像度が入ってきます。GLSL オンラインエディタの場合にはスクリーンの一辺は縦横ともに 512px ですので、上記の vec2 型変数 r には (512.0, 512.0) という感じでデータが入っています。
同様に gl_FragCoord にも、なにかしらの数値が入っています。GLSL で今回のように映像を作り出す場合には、スクリーン上の すべてのピクセルに対して一律に同じシェーダのコードが実行 されます。gl_FragCoord は、今まさに処理されようとしているピクセルの座標を教えてくれる便利な組み込みの変数です。
ここまでを踏まえて先ほどのコードをもう一度よく見てみましょう。
先ほどのような計算を行うとスクリーンの中心を原点として X と Y のそれぞれが -1.0 〜 1.0 となるような座標系を作ることができます。左下の隅が (-1.0, -1.0) となり、同じように右上の隅が (1.0, 1.0) となります。
最終的に、先ほどのコードでいうところの変数 p には これからまさに処理されようとしているスクリーン上の座標 が、-1.0 〜 1.0 の範囲で入っている状態になりますね。
ただこのままでは、二次元のスクリーン上の X と Y 座標についてのみでしか考えられない状態になっています。ここに奥行きに関する情報を追加して、レイを三次元空間上に解き放ってあげましょう。
vec3 direction = normalize(vec3(p.x, p.y, -1.0));
ベクトルを normalize で正規化しているのがポイントになるでしょうか。座標系は右手系と同じで奥に行くほど Z 値はマイナスになります。上記のコードは実際には、レイを飛ばしているというよりはレイの進む方向を定めるための処理ですね。レイがどこに向かって進んでいくかがこれで決まりました。
とりあえず色出してみっか!!
スクリーンの座標からレイを定義するための方向に関する情報は先ほどまでの手順で生成できました。
レイにはその向かう方向以外に、レイの 始点となる座標 が必要になります。ここは別々の変数として定義してももちろん構わないのですが、GLSL では構造体が定義できますのでこれを利用してみましょう。
struct Ray{
vec3 origin; // 始点
vec3 direction; // 方向
};
これで、レイの始点と進行方向のふたつを一度に管理できるようになりましたね。
それでは先程までのコードを統合して、レイの情報を色として出力するところまでを書いてみましょう。
precision mediump float;
uniform float t;
uniform vec2 r;
struct Ray{
vec3 origin;
vec3 direction;
};
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
// ray init
Ray ray;
ray.origin = vec3(0.0, 0.0, 5.0);
ray.direction = normalize(vec3(p.x, p.y, -1.0));
gl_FragColor = vec4(ray.direction, 1.0);
}
最終的に gl_FragColor に出力した情報が色として画面に出るようになります。色は RGBA の四つの要素で指定するので vec4 を使っているのがポイントでしょうか。
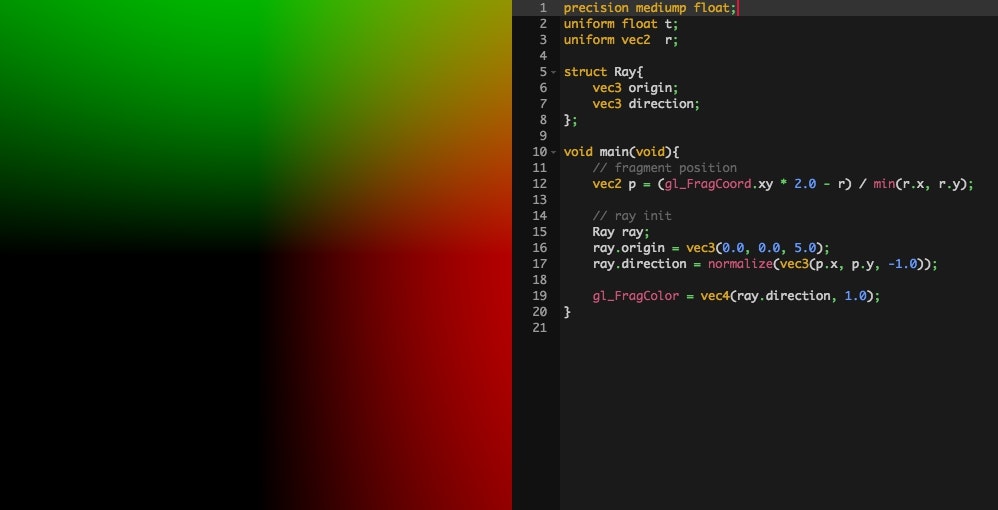
これを実行すると次のような結果になります。
色は 0.0 〜 1.0 の範囲で指定するので、例えば X 座標がマイナスとなる左半分には赤色の成分がまったく出力されていないのがわかるでしょうか。逆に右側に行けば行くほど赤色が濃くなっていますね。うまく、レイの座標が色として出力されており、レイの定義もうまくいっているのがわかります。
とりあえず球出してみっか!!!
レイトレで一番最初にレンダリングするものといえばやっぱり球ちゃんです。
全国 1 億 7120 万人のレイトレファンの諸兄におかれましてもまずは球ちゃんからレンダリングしたことと思います。
レイトレーシングの手法の一つである レイマーチング の場合は、球ちゃんを描くのは非常に簡単でした。レイトレーシングで球を出すのはレイマーチングと同様に基本中の基本ではあるものの、レイマーチングの場合と比較すると若干手数が増えます。どちらかというとレイマーチングの場合が簡素すぎますね。
今回は球の定義もレイの場合と同じように構造体を使ってみましょう。
struct Sphere{
float radius; // 半径
vec3 position; // 位置
vec3 color; // 色
};
簡単ですね。意味もそのままですのでわかりやすいと思います。
それでは、上記の構造体を使って球体を定義し、実際にレイと球との交差判定を行ってみましょう。交差判定には、専用の関数を定義してみることにしましょうか。
引数として、レイと球体、そのふたつを受け取って交差判定を行う関数です。
bool intersectSphere(Ray R, Sphere S){
vec3 a = R.origin - S.position;
float b = dot(a, R.direction);
float c = dot(a, a) - (S.radius * S.radius);
float d = b * b - c;
if(d > 0.0){
float t = -b - sqrt(d);
return (t > 0.0);
}
return false;
}
引数をふたつ受け取って、結果を真偽値で返す関数になっているのがわかると思います。第一引数には定義したレイを、第二引数に球体の定義を渡します。
肝心の関数の中身で何をやっているのかですが、ここは完全に数学の世界です。レイトレについて調べてみれば、どうしてこのような計算で球体とレイとの交差判定が行えるのかはわかると思います。あえて言うと、最終的に変数 t の中に入る値が 0.0 より大きければ交差しているということになるのがポイントです。
計算方法の解説については以下のページなどを参考にするといいと思います。特に最上段のリンクは WebGL によるライブデモも用意されていて非常にわかりやすいと思います。
さて、それでは先程の交差判定関数を用いて、実際にどのようにシェーダを記述したらいいのか見てみましょう。実際に動作するコードは次のような感じになります。
precision mediump float;
uniform float t;
uniform vec2 r;
struct Ray{
vec3 origin;
vec3 direction;
};
struct Sphere{
float radius;
vec3 position;
vec3 color;
};
bool intersectSphere(Ray R, Sphere S){
vec3 a = R.origin - S.position;
float b = dot(a, R.direction);
float c = dot(a, a) - (S.radius * S.radius);
float d = b * b - c;
if(d > 0.0){
float t = -b - sqrt(d);
return (t > 0.0);
}
return false;
}
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
// ray init
Ray ray;
ray.origin = vec3(0.0, 0.0, 5.0);
ray.direction = normalize(vec3(p.x, p.y, -1.0));
// sphere init
Sphere sphere;
sphere.radius = 1.0;
sphere.position = vec3(0.0);
sphere.color = vec3(1.0);
// hit check
vec3 destColor = vec3(0.0);
if(intersectSphere(ray, sphere)){
destColor = sphere.color;
}
gl_FragColor = vec4(destColor, 1.0);
}
すごく長いコードのように見えると思いますが、ここまで小さく区切って解説してきたものを繋ぎ合わせているだけですので、落ち着いて考えてみてください。
レイと球を定義して、交差判定関数を呼んでいるのがわかりますね。戻り値は真偽値なので、その値に応じて最終的に出力される色を格納する destColor の中身を変えているのが見て取れます。
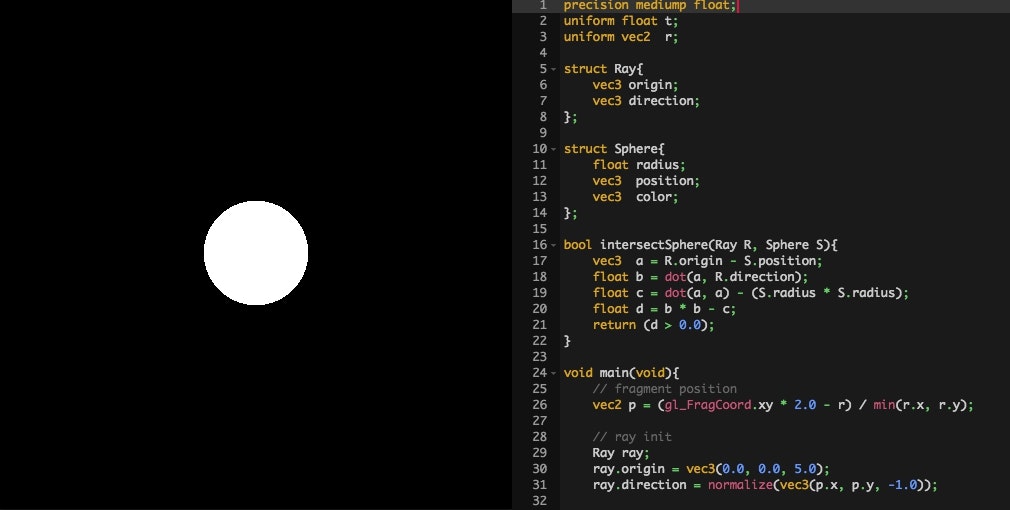
これを実行すると、次のような感じになるはずです。
白い球ちゃん出てますね!
とりあえず陰影つけてみっか!!!!
先ほどの実行結果では、なんとなく球ちゃんが出ている感じはしますがベタ塗り状態なので球体というより円という感じになってしまっていました。ちゃんと三次元空間で立体としての球と交差判定がとれているのかどうか確認するために、球の法線を求めて陰影をつけてみましょう。
球の法線を求めるのは、理屈としてはすごく簡単です。
レイと球とが交差した 交点 さえ求まれば、球の中心からその交点に向かってベクトルを伸ばしてやればいいんですね。これはよ〜く頭を柔らかくして考えてみれば自ずとわかると思います。
実際にそのような処理をコードに反映させていくわけですが、交点の情報などを包括的に扱うための構造体を一つ定義して、そこに交差に関する情報が集約されるように設計してみましょう。
struct Intersection{
bool hit; // 交差したかどうかのフラグ
vec3 hitPoint; // 交点の座標
vec3 normal; // 交点位置の法線
vec3 color; // 交点位置の色
};
上記は、交差に関する情報をまとめて持つことができる構造体 Intersection です。
これを見ると、まずレイと衝突したのかどうかという情報を格納する hit があり、その他に交点の位置やその地点の法線などが同時に格納できるようになっているのがわかりますね。
交差判定関数を修正して、上記の構造体にデータを格納して返すようにしてみます。
Intersection intersectSphere(Ray R, Sphere S){
Intersection i;
vec3 a = R.origin - S.position;
float b = dot(a, R.direction);
float c = dot(a, a) - (S.radius * S.radius);
float d = b * b - c;
if(d > 0.0){
float t = -b - sqrt(d);
if(t > 0.0){
i.hit = true;
i.hitPoint = R.origin + R.direction * t;
i.normal = normalize(i.hitPoint - S.position);
float d = clamp(dot(normalize(vec3(1.0)), i.normal), 0.1, 1.0);
i.color = S.color * d;
return i;
}
}
i.hit = false;
i.hitPoint = vec3(0.0);
i.normal = vec3(0.0);
i.color = vec3(0.0);
return i;
}
関数の戻り値の型が Intersection になっているのがわかるでしょうか。
関数の中身は、途中までは先程の衝突判定の関数そのままです。先程は変数 t が 0.0 以上かどうかをそのまま真偽値として返していましたが、今回はそこから更に処理が分岐するようになっています。
そして、もし衝突していると判断できる場合には、まず交差した座標までの距離を求めてやります。これが変数 t ですね。距離が求まったら、それをレイの始点と方向とを利用して計算してやることで、最終的に交点の座標位置を求めているわけですね。
交点の座標が求まったら、球体の中心部分の座標と比較することで法線を求め、そのまま内積でディフューズを計算しています。一度にたくさんの処理が詰め込まれていますが、落ち着いて順番にコードを追いかけながら考えてみればそれほど究極に難しいことをやっているという感じではないと思います。
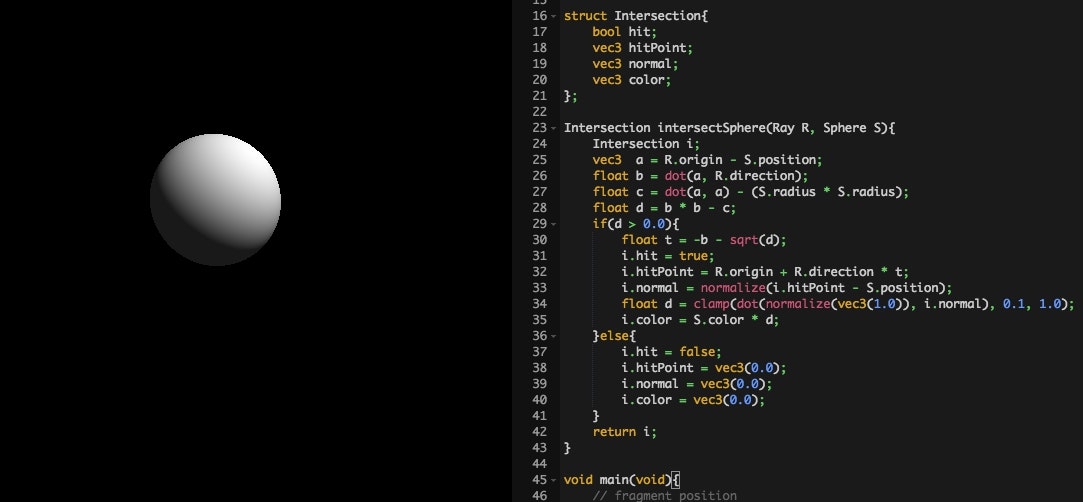
それではこれを実行するとどうなるのか、実際の描画結果の様子を見てみましょう。
見事に陰影がつきましたね。
正しく交差判定や法線の算出ができていることが確認できました。
とりあえず床とか出して鏡面反射してみっか!!!!!
さて、レイトレーシングといえばあれですね。ピカピカの鏡のような鏡面反射で描かれるオブジェクトですね。
複数のオブジェクトや床などが配置されていないと効果がわかりにくいですから、これらのものをまずは用意してやらないといけません。一つ一つを丁寧に解説しているととてもじゃないけど 尺が足りない 気がするので、概念だけサクッと解説します。
※いずれ wgld.org でちゃんと解説記事書きます……
床を出す場合には、平面とレイとの間で、先ほどの球と同じように交差判定をしてやればいいですね。計算の方法などは少々違いますが、要はやるべきことは同じです。また、先ほどの実装を思い返してみればわかるとおり、球体を独自の構造体として定義してありますから球を複製することは簡単にできます。
その辺りを踏まえて、複数の球ちゃんと床ちゃんをまずは描画することを目指してみましょう。
注意すべきポイントとしては、今回の場合はすべてのオブジェクトとの交差判定を行うことになりますので、レイの方向によっては複数のオブジェクトに交差するケースが出てくる可能性があり、このことを踏まえた実装ができるかどうかが鍵になります。
具体的には、交差と判定された場合に、しっかりとオブジェクトまでの距離を考慮して、最も近い距離にあるオブジェクトの色や情報を拾ってくるようにすることでしょう。その辺りに注意して実装してみるとこんなかんじになるでしょうか。
precision mediump float;
uniform float t;
uniform vec2 r;
struct Ray{
vec3 origin;
vec3 direction;
};
struct Sphere{
float radius;
vec3 position;
vec3 color;
};
struct Plane{
vec3 position;
vec3 normal;
vec3 color;
};
struct Intersection{
vec3 hitPoint;
vec3 normal;
vec3 color;
float distance;
};
const vec3 lightDirection = vec3(0.577);
void intersectSphere(Ray R, Sphere S, inout Intersection I){
vec3 a = R.origin - S.position;
float b = dot(a, R.direction);
float c = dot(a, a) - (S.radius * S.radius);
float d = b * b - c;
float t = -b - sqrt(d);
if(d > 0.0 && t > 0.0 && t < I.distance){
I.hitPoint = R.origin + R.direction * t;
I.normal = normalize(I.hitPoint - S.position);
d = clamp(dot(lightDirection, I.normal), 0.1, 1.0);
I.color = S.color * d;
I.distance = t;
}
}
void intersectPlane(Ray R, Plane P, inout Intersection I){
float d = -dot(P.position, P.normal);
float v = dot(R.direction, P.normal);
float t = -(dot(R.origin, P.normal) + d) / v;
if(t > 0.0 && t < I.distance){
I.hitPoint = R.origin + R.direction * t;
I.normal = P.normal;
float d = clamp(dot(I.normal, lightDirection), 0.1, 1.0);
float m = mod(I.hitPoint.x, 2.0);
float n = mod(I.hitPoint.z, 2.0);
if((m > 1.0 && n > 1.0) || (m < 1.0 && n < 1.0)){
d *= 0.5;
}
float f = 1.0 - min(abs(I.hitPoint.z), 25.0) * 0.04;
I.color = P.color * d * f;
I.distance = t;
}
}
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
// ray init
Ray ray;
ray.origin = vec3(0.0, 2.0, 6.0);
ray.direction = normalize(vec3(p.x, p.y, -1.0));
// intersection init
Intersection i;
i.hitPoint = vec3(0.0);
i.normal = vec3(0.0);
i.color = vec3(0.0);
i.distance = 1.0e+30;
// sphere init
Sphere sphere[3];
sphere[0].radius = 0.5;
sphere[0].position = vec3(0.0, -0.5, sin(t));
sphere[0].color = vec3(1.0, 0.0, 0.0);
sphere[1].radius = 1.0;
sphere[1].position = vec3(2.0, 0.0, cos(t * 0.666));
sphere[1].color = vec3(0.0, 1.0, 0.0);
sphere[2].radius = 1.5;
sphere[2].position = vec3(-2.0, 0.5, cos(t * 0.333));
sphere[2].color = vec3(0.0, 0.0, 1.0);
// plane init
Plane plane;
plane.position = vec3(0.0, -1.0, 0.0);
plane.normal = vec3(0.0, 1.0, 0.0);
plane.color = vec3(1.0);
// hit check
intersectSphere(ray, sphere[0], i);
intersectSphere(ray, sphere[1], i);
intersectSphere(ray, sphere[2], i);
intersectPlane(ray, plane, i);
gl_FragColor = vec4(i.color, 1.0);
}
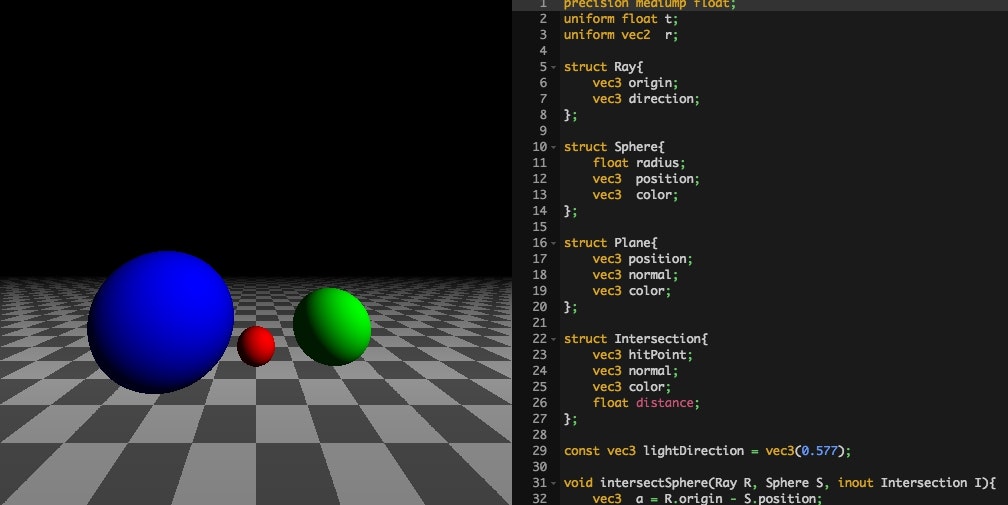
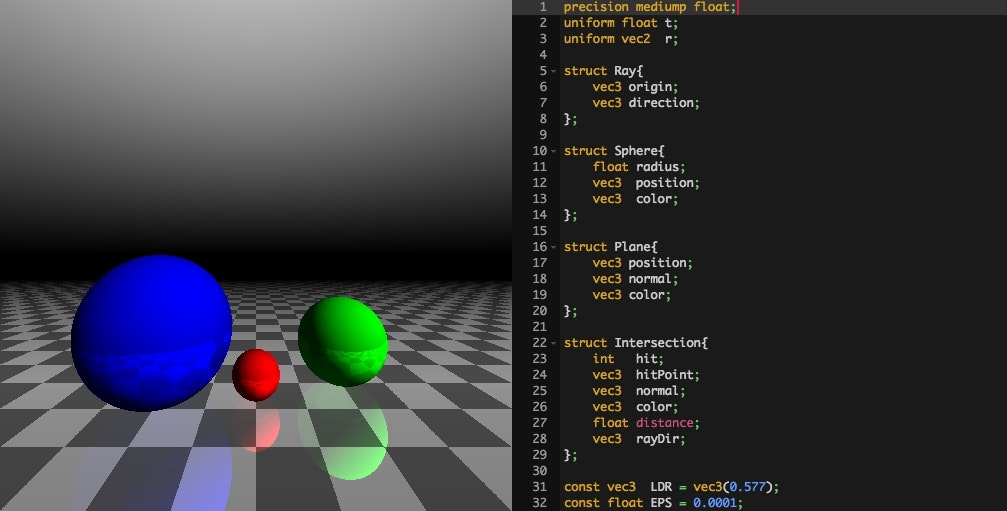
こんなふうになればいいですね。
ここまで来ると、複数のモデルを同時に描くことができていますから、あとはそれぞれが相互に反射し合い風景が映り込むような状況をうまく再現してやればいいことになります。
あたかも現実世界の光と同じように、オブジェクトにぶつかったらレイが反射して、その反射した先にオブジェクトがあればそのオブジェクトの様子を加味した色に調整してやって……を繰り返すわけですね。
基本的に、レイが反射する回数は無限というわけにはいきませんから、そのあたりはどこかで落とし所を見つけないといけません。その辺りも踏まえつつ考えてみると、鏡面反射するシーンを描くことができるのではないでしょうか。
以下のサンプルの場合には、レイが反射する回数は定数として定義しておき、それを指標にして処理を行っています。
precision mediump float;
uniform float t;
uniform vec2 r;
struct Ray{
vec3 origin;
vec3 direction;
};
struct Sphere{
float radius;
vec3 position;
vec3 color;
};
struct Plane{
vec3 position;
vec3 normal;
vec3 color;
};
struct Intersection{
int hit;
vec3 hitPoint;
vec3 normal;
vec3 color;
float distance;
vec3 rayDir;
};
const vec3 LDR = vec3(0.577);
const float EPS = 0.0001;
const int MAX_REF = 4;
Sphere sphere[3];
Plane plane;
void intersectInit(inout Intersection I){
I.hit = 0;
I.hitPoint = vec3(0.0);
I.normal = vec3(0.0);
I.color = vec3(0.0);
I.distance = 1.0e+30;
I.rayDir = vec3(0.0);
}
void intersectSphere(Ray R, Sphere S, inout Intersection I){
vec3 a = R.origin - S.position;
float b = dot(a, R.direction);
float c = dot(a, a) - (S.radius * S.radius);
float d = b * b - c;
float t = -b - sqrt(d);
if(d > 0.0 && t > EPS && t < I.distance){
I.hitPoint = R.origin + R.direction * t;
I.normal = normalize(I.hitPoint - S.position);
d = clamp(dot(LDR, I.normal), 0.1, 1.0);
I.color = S.color * d;
I.distance = t;
I.hit++;
I.rayDir = R.direction;
}
}
void intersectPlane(Ray R, Plane P, inout Intersection I){
float d = -dot(P.position, P.normal);
float v = dot(R.direction, P.normal);
float t = -(dot(R.origin, P.normal) + d) / v;
if(t > EPS && t < I.distance){
I.hitPoint = R.origin + R.direction * t;
I.normal = P.normal;
float d = clamp(dot(LDR, I.normal), 0.1, 1.0);
float m = mod(I.hitPoint.x, 2.0);
float n = mod(I.hitPoint.z, 2.0);
if((m > 1.0 && n > 1.0) || (m < 1.0 && n < 1.0)){
d *= 0.5;
}
float f = 1.0 - min(abs(I.hitPoint.z), 25.0) * 0.04;
I.color = P.color * d * f;
I.distance = t;
I.hit++;
I.rayDir = R.direction;
}
}
void intersectExec(Ray R, inout Intersection I){
intersectSphere(R, sphere[0], I);
intersectSphere(R, sphere[1], I);
intersectSphere(R, sphere[2], I);
intersectPlane(R, plane, I);
}
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
// ray init
Ray ray;
ray.origin = vec3(0.0, 2.0, 6.0);
ray.direction = normalize(vec3(p.x, p.y, -1.0));
// sphere init
sphere[0].radius = 0.5;
sphere[0].position = vec3(0.0, -0.5, sin(t));
sphere[0].color = vec3(1.0, 0.0, 0.0);
sphere[1].radius = 1.0;
sphere[1].position = vec3(2.0, 0.0, cos(t * 0.666));
sphere[1].color = vec3(0.0, 1.0, 0.0);
sphere[2].radius = 1.5;
sphere[2].position = vec3(-2.0, 0.5, cos(t * 0.333));
sphere[2].color = vec3(0.0, 0.0, 1.0);
// plane init
plane.position = vec3(0.0, -1.0, 0.0);
plane.normal = vec3(0.0, 1.0, 0.0);
plane.color = vec3(1.0);
// intersection init
Intersection its;
intersectInit(its);
// hit check
vec3 destColor = vec3(ray.direction.y);
vec3 tempColor = vec3(1.0);
Ray q;
intersectExec(ray, its);
if(its.hit > 0){
destColor = its.color;
tempColor *= its.color;
for(int j = 1; j < MAX_REF; j++){
q.origin = its.hitPoint + its.normal * EPS;
q.direction = reflect(its.rayDir, its.normal);
intersectExec(q, its);
if(its.hit > j){
destColor += tempColor * its.color;
tempColor *= its.color;
}
}
}
gl_FragColor = vec4(destColor, 1.0);
}
どうでしょうか。
反射や複数オブジェクトの描画については詳細を解説してはいませんが、要は応用です。最初の球に陰影がつくところまで持ってこれれば、あとは創意工夫あるのみです。
全国 7 億 1200 万人のレイトレファンの皆様であれば、この辺りは簡単でしょう。
まとめ
さて長々と書いてきましたがいかがでしたか。
冒頭にも書いたとおりで、いわゆる普通の WebGL 実装と比べると、今回の内容は考え方そのものがまったく違いますね。
すべてのピクセルに対して同じように実行されるシェーダのコードを工夫するだけで、こんなふうにリアルな 3DCG が描き出せるというのはなんとも不思議です。シェーダコーディングに独特の、この不思議な感覚を楽しいと感じることができたなら、あなたも立派なレイトレファンの一人です。
レイトレはけして簡単ではありません。実を言えば私もそんなにレイトレには詳しくなくて、なんとかどうにかこうにか今回のデモを完成させた次第です。大したデモでもないのですが、レイトレーシングのその魅力の一端を感じていただけたなら幸いです。
気軽に始めることができる WebGL + GLSL のシェーダコーディング。ぜひ、チャレンジしてみてください。