1つの巨大な数を掲示するだけで合否発表を行うシステムを構築してみた

はじめに

この記事は先日Twitter上で見た リア充の補集合@complement_real さん の とあるツイート に着想を得ています。
その内容は以下の通りです。

受験番号をあらかじめ素数だけにしておけば、合否発表は1つの巨大な合成数を掲示するだけで済む。

このシステムをPythonで実装してみます。

受験番号の生成

まず、素数だけの受験番号列を生成しなければなりません。ここでは分かりやすく数字が若い順の素数列として生成します。つまり、受験番号は$2,3,5,7,11,13,17,...$という風に割り当てられることにします。

素数ジェネレータを使う

素数の生成は自分で実装しても良いのですが、ここは先人達の知恵を借りましょう。@Mokkeee さんの 素数ジェネレータ(python) を使います。エラトステネスの篩 の原理を用いて高速化されています。

prime_generator.py

def primes(max_number):
    """
    指定値未満の素数を取得するジェネレータ
    :param max_number: 最大値
    :return: 素数ジェネレータ
    """
    if max_number <= 2:
        raise StopIteration
    yield 2
    is_prime = [1] * max_number
    square_root_of_max = max_number ** 0.5
    for number in range(3, max_number, 2):
        if is_prime[number] is 0:
            continue
        yield number
        if number <= square_root_of_max:
            for multiple in range(number * 2, max_number, number):
                is_prime[multiple] = 0

n番目の素数はどれくらい？

上で示した素数ジェネレータは「引数で与えた整数までの素数列」を生成するものです。しかし、このシステムでは「n人分の受験番号(素数列)を生成したい」わけですから、そのまま使えるわけではありません。
この問題を解決するためにはn番目の素数がどれくらいの値になるかを推定する必要があります。そこで素数計数関数 $\pi(x)$ を導入します。これは実数$x$以下の素数の個数を表す関数です。ただ、この関数を直接計算するのは難しいので漸近近似関数 $\frac{x}{\ln x}$ を使います。この関数には以下の性質があります。

\lim_{x \to \infty} \frac{\pi(x)}{\frac{x}{\ln x}} = 1~~~,~~~\frac{x}{\ln x} < \pi(x)~(x\geqq 17)

つまり、n番目までの素数列を生成したいときは $\frac{x}{\ln x} = n$ となるような$x$を求めて、$x$を素数ジェネレータの引数に与えればよいということです。
Pythonの代数計算モジュールsympyでは方程式を解く機能があるので求める$x$の値を計算できます。試しに300番目の素数がどれくらいの値になるかを求めてみます。

.py

import sympy as sym
x=sym.symbols('x')
limit=sym.solve(x/sym.log(x)-n)[1].evalf() #方程式の解は2つあるが、片方は不適なので適当な方を選択している
print(limit)
# 2325.50815687053

実際、300番目の素数は1987なのであまり無駄なく求めたい$x$を求めることができています。

さて、$\frac{x}{\ln x} < \pi(x)$という性質は$x\geqq 17$のときのみ成り立ちます。17未満の素数は$2,3,5,7,11,13$の6個なので$6\geqq n$のときは$x=13$としておけばよいでしょう¹。

受験番号を生成する

以上のことを踏まえてn人分の受験番号を生成する関数Identification_numbers(n)を実装します。

.py

import sympy as sym
def Identification_numbers(n):
    x=sym.symbols('x')
    limit=sym.solve(x/sym.log(x)-n)[1].evalf() if n > 6 else 12 #三項演算子
    return [prime for prime in list(primes(int(limit)+1))[:n]] #n人分の受験番号リスト

print(Identification_numbers(10))
# [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

CSVで管理する

関係者じゃないので実際の試験処理現場がどうなっているかは分かりませんが、個人的な偏見としてExcel使ってそうだなと思ったのでCSVで色々することを想定して実装します。

受験番号の出力

受験番号をCSV形式で出力します。受験者が300人の場合のコードを示します。CSV出力用にIdentification_numbers(n)を若干いじります。

.py

import csv
import sympy as sym
def Identification_numbers(n):
    x=sym.symbols('x')
    limit=sym.solve(x/sym.log(x)-n)[1].evalf() if n > 6 else 12 #三項演算子
    return [[prime] for prime in list(primes(int(limit)+1))[:n]] #n人分の受験番号リスト

output = [["受験番号"]] + Identification_numbers(300)
with open('Identification_numbers.csv', 'w',newline='') as f:
    writer = csv.writer(f)
    writer.writerows(output)

こんな感じで出力できます。

合否の入力

受験番号の列の隣に「合否」の列をつくり、合格なら「合格」、不合格なら「不合格」と(CSV上で)入力していきます。
今回は300人受けて150人くらい受かるとして合否を入力しました²。

合否の読み込み

合否を入力したCSVファイルを読み込んで合格者リストをつくります。

.py

import csv
with open('Identification_numbers.csv') as f:
    reader = csv.reader(f)
    for read in reader:
        Pass_members=[read[0] for read in reader if read[1] == "合格"]

print(Pass_members)
# ['5', '7', '19', (中略), '1861', '1873', '1879', '1931', '1979']

CSVと比較したところ、ちゃんと読み込めているようでした。

合否発表のための巨大合成数生成

さきほど作ったCSVファイルから合否を読み取って合否発表用の1つの巨大な合成数を計算します。

.py

import csv
Pass_number=1
with open('.csv') as f:
    reads = csv.reader(f)
    for read in reads:
        if read[1] == "合格":
            Pass_number *= int(read[0])
            
print(f'合否番号は{Pass_number}です。')
# 合否番号は17728767970985829481823989896077530418008762861093568590799175395949804988859166709548172634300750777203816150616084022278825967640983715427906599975153909704333007620526920040620833373826002627639097716395602011631222317500372015045014286851683269585639799950385605591874823197860959531943088725049707709238936182671598532448798706594027194223073302624361519182895822859980047928855121437589068869289504173391055です。

合否発表用の413桁の巨大合成数が生成できました。

合否判定プログラム

このシステムの特性上、巨大合成数が受験番号で割り切れれば合格、割り切れなければ不合格です。では合否判定プログラムを実装しましょう。

.py

def judge(PassNumber):
    print("あなたの受験番号を入力してください。",end='')
    Num = int(input(">"))
    print(f'あなたは{"不"*(PassNumber % Num != 0)}合格です。')

日本で一番大規模な試験のシミュレーション

ここまでは300人受験して150人受かるという想定で書いてきました。しかし、もっと大規模な試験というのは多く存在するでしょう。このシステムがどこまで対応しているのかを調べておく必要がありそうです。

日本で最も受験者数の多い大学は近畿大学で、毎年15万人以上が受験するそうです。また、学生数日本最多の日本大学は約7万人の学部生が在籍しているそうです。単純に1学年あたりにすると1.8万人程度です。
このことから、受験の仕組みが良く分からないので適当ですが、とりあえず16万人受験して2万人が受かる状況のシミュレーションができれば日本の試験にはほぼ対応したことになるのではないでしょうか。

Excelの限界

Excelは最大で1,048,576 行、16,384 列まで扱えます。今回のシミュレーションで必要なのは16万1行、2列なのでExcelの許容範囲内です。

実際にやってみた。

ここまでで示したコードを用いて、16万人受験して2万人が合格することを想定したシミュレーションを行いました。流石に16万項目について一つ一つ「合格」と「不合格」を入力するわけにはいかないので、Excelで「=IF(RANDBETWEEN(1,8)=1,"合格","不合格")」をオートフィルしました。合格率を1/8としているだけなので実際の合格者は2万人ピッタリではありません。

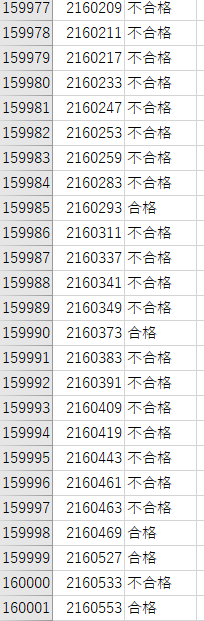
合否判定用の115,351桁の巨大合成数65456117423983939(中略)98890283367615106の取得にも成功し、合格判定もできました。

合格判定

あなたの受験番号を入力してください。
>2160553
あなたは合格です。

というわけで、日本の試験はほぼ全てこの方式で運用できることが分かりましたね。

お手軽シミュレーター

実際に運用する時にCSV形式でいじれたらいいかなと思い、CSV出力やCSV入力を前提としていますが、シミュレートするときに一々CSVをいじるのが面倒だったので、Python上だけでなんちゃってシミュレーションができるようにしました。

.py

import random
import sympy as sym
def primes(max_number):
    """
    指定値未満の素数を取得するジェネレータ
    :param max_number: 最大値
    :return: 素数ジェネレータ
    """
    if max_number <= 2:
        raise StopIteration
    yield 2
    is_prime = [1] * max_number
    square_root_of_max = max_number ** 0.5
    for number in range(3, max_number, 2):
        if is_prime[number] is 0:
            continue
        yield number
        if number <= square_root_of_max:
            for multiple in range(number * 2, max_number, number):
                is_prime[multiple] = 0

def Identification_numbers(n):
    x=sym.symbols('x')
    limit=sym.solve(x/sym.log(x)-n)[1].evalf() if n > 6 else 12 #三項演算子
    return [prime for prime in list(primes(int(limit)+1))[:n]] #n人分の受験番号リスト

def simulate():
    print("受験者数を入力してください。",end='')
    examinees = int(input(">"))
    print("合格者数を入力してください。",end='')
    successfulExaminees = int(input(">"))
    
    PassMembers=random.sample(Identification_numbers(examinees),successfulExaminees)

    PassNumber = 1
    for Num in PassMembers:
        PassNumber *= Num
    
    print(f'合否番号は{PassNumber}です。')
    
    while(True):
        print(f'合否判定をしたい受験番号を入力してください。シミュレーションを終了する場合は\'z\'と入力してください。',end='')
        judgeNum = input(">")
        if judgeNum=="z":break
        print(f'受験番号{judgeNum}は{"不"*(PassNumber % int(judgeNum) != 0)}合格です。')
    
simulate()

実行例

受験者数を入力してください。
>1500
合格者数を入力してください。
>1000
合否番号は93924305033683184(中略)2955393315122183987094です。
合否判定をしたい受験番号を入力してください。シミュレーションを終了する場合は'z'と入力してください。
>2
受験番号2は合格です。
合否判定をしたい受験番号を入力してください。シミュレーションを終了する場合は'z'と入力してください。
>31
受験番号31は合格です。
合否判定をしたい受験番号を入力してください。シミュレーションを終了する場合は'z'と入力してください。
>9203
受験番号9203は合格です。
合否判定をしたい受験番号を入力してください。シミュレーションを終了する場合は'z'と入力してください。
>z

おわりに

「システム」とまで言えるかわかりませんが、自分がやりたかったことは実現できました。

実用性皆無かと思いきや、例えば16万人中2万人の合格者の受験番号を全て掲示するには(受験番号が1,2,3,...,160000という風に単純に割り当てられていたとして)10万桁程度は必要となるので今回取得した約11万桁の巨大合成数と大差ありませんし、掲示されている番号列の中に受験番号と一致する番号があるかを確かめること(同値性の確認)と、ある数をある数で割り切れるかどうかの確認では、後者の方が一般に簡単なので、巨大合成数掲示方式の方が効率的なのかも...と思いました(コンピュータでの話なので人間が合否確認するなら前者の方がいいでしょうが)。
ちなみに、1つの巨大な数を掲示する方法で、もっと効率の良い方法を件のツイートのリプライツリーで見つけたので番外編で扱います。

この記事を書くために必要だった時間の大半は素数の勉強時間でした。難しい...

誤字脱字や誤った記述、更に良いアルゴリズム、気づいたこと、分かりにくい箇所、感想などがあればぜひコメントをください。

1. もっと場合分けすれば無駄が省けますが、ここは簡単に$x=13$としておきます。 ↩

2. 実際に300人分入力したわけではなく「=IF(RANDBETWEEN(1,2)=1,"合格","不合格")」をオートフィルして擬似的に合否を入力しています(CSV形式で保存すると値のみ保存されます)。 ↩