プログラミング初心者がアイスクリームの消費量を回帰分析してみた

1. About me

• 「最新の技術に触れたい」「新しいフィールドでチャレンジしたい」という思いから、6年間勤めた銀行を退職しました。

• プログラミングやITに関する知識は皆無の状態でしたが、エンジニアへの転職を目指してAidemy（データ分析コース・3ヶ月)を受講開始しました（2022/06〜現在）。

2. 本記事の概要

• scikit-learnで気象データ（日平均気温・日照時間・降水量）からアイスクリーム¹の消費量を予測するモデルを構築しました。

• アイスムリームの消費量を測る尺度として、ice cream rate = アイスクリームへの支出額（円) / 食料支出(円)を使用しています。

• 目的はアウトプット実践と知識の定着です。

1. 実行環境

• PC : MacBook Air (M1, 2020)
• 実行環境 : Google Colaboratory

2. 使用したデータ

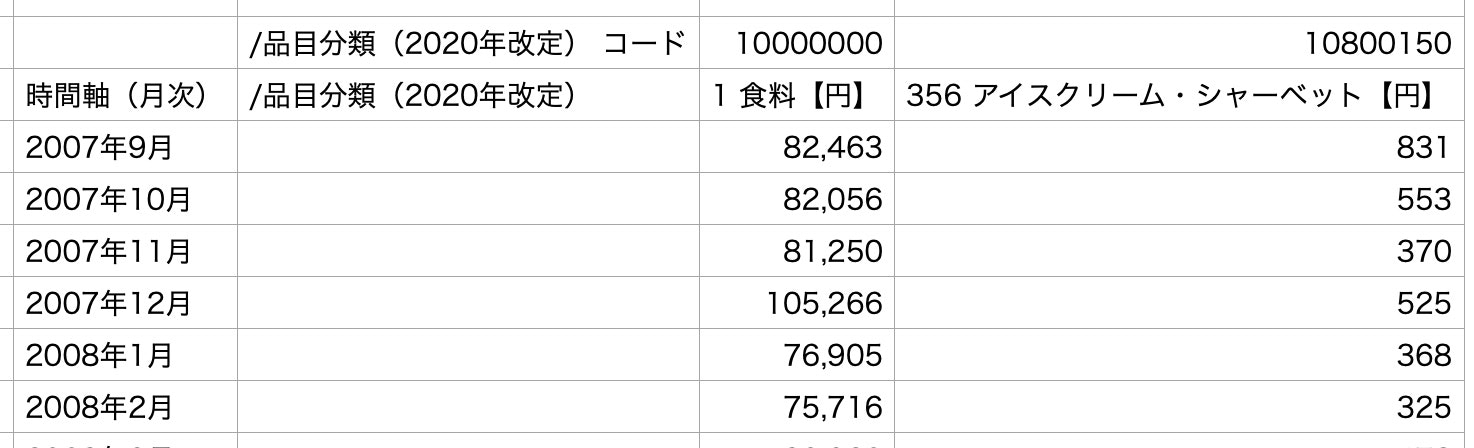
• 東京都の世帯当たりの食料支出、アイスクリームへの支出に関する月次データ :
  e-StatからダウンロードしたCSVファイルを読み込みしています。
  

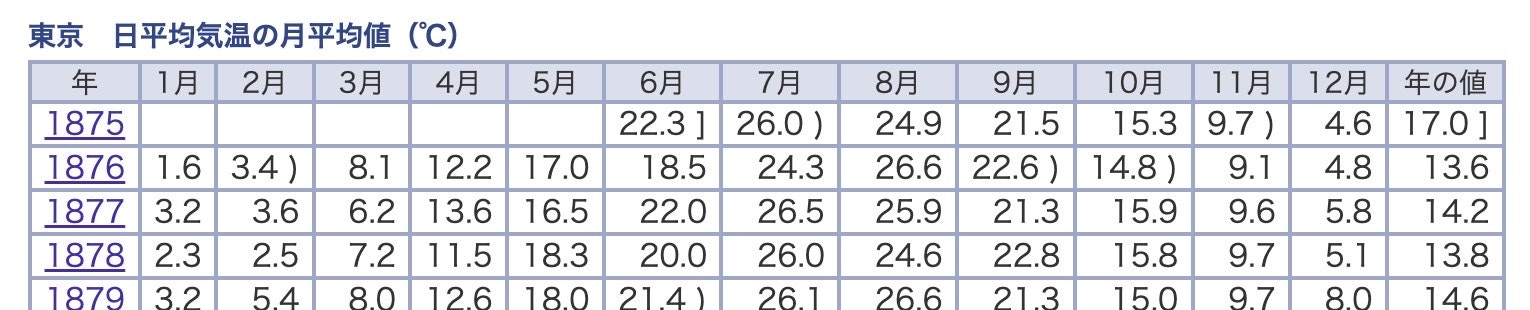
• 東京都の気象データ :
  気象庁HP上に掲載されているデータテーブルを読み込みしています。
  

3. 作成したプログラム

1. データの読み込み

アイスクリームの消費量に関するデータを読み込みしていきます。

import numpy as np
import pandas as pd
from pandas import datetime

filepath = "/content/アイスクリーム売上データ.csv"
# csv読み込み時にDatetimeIndexを設定します
df = pd.read_csv(filepath, header=9, usecols=[7,9,10], index_col=0, parse_dates=True,
                        date_parser=lambda x: pd.to_datetime(x, format='%Y年%m月'), encoding="shift-jis")
# カラム名を分かりやすいように変更します
df.set_axis(['食料支出', 'アイスクリームへの支出'], axis=1, inplace=True)
# データ型を統一します
df['食料支出'] = df['食料支出'].str.replace(',', '').astype(np.float64)
df['アイスクリームへの支出'] = df['アイスクリームへの支出'].str.replace(',', '').astype(np.float64)
# 「ice cream rate」カラム（列）を追加します
df['ice cream rate'] = df['アイスクリームへの支出'] / df['食料支出'] 
# 学習に用いないカラム（列）を削除します
drop_col = ['食料支出', 'アイスクリームへの支出']
df = df.drop(drop_col, axis=1)

df.head()

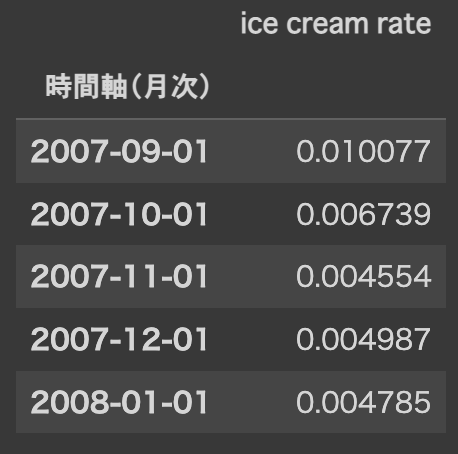
これでDatetimeIndexを持つData Frameが出来上がりました。

2. 気象データの追加

作成したData Frameに気象データを追加していきます。
まずは平均気温(average temperature)からです。Webスクレイピングによりデータを取得しています。

# 気象庁HP
url_at = 'https://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s3.php?prec_no=44&block_no=47662&year=&month=&day=&view=a1'
# HP上のデータテーブル（HTML)を読み込みします
l_at = pd.read_html(url_at) # 取得したDataFrameはListに格納されます
# ListからDataFrameを取得し、2007年9月以降のデータを抽出します
df_at = l_at[0].T.iloc[:,132:]

# Date　Frameにカラム（列）として追加する為に、データをSeriesとして格納していきます
# まず2007年9月〜2007年12月のデータを格納
s_at = df_at.iloc[9:13,0] 
# for文で2008年1月〜2021年12月のデータを格納
for i in range(1,15): 
  s_at = pd.concat([s_at,df_at.iloc[1:13,i]])
# 最後に2022年1月〜2022年6月のデータを格納
s_at = pd.concat([s_at,df_at.iloc[1:7,15]])
# Date Frameに「average temperature」カラム（列）を追加します
df['average temperature']= s_at.values.astype(np.float64)

df.head()

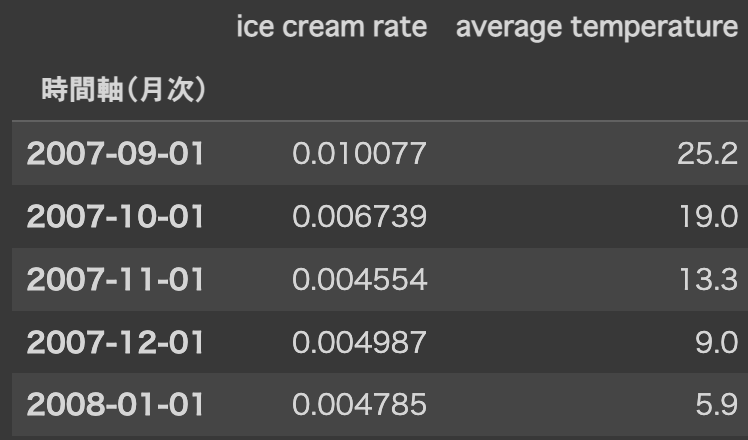
同様に日照時間(sunshine time)、降水量(rain)のデータをdfに追加します。

# 日照時間(sunshine time)
url_st = 'https://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s3.php?prec_no=44&block_no=47662&year=&month=&day=&view=p4'
l_st = pd.read_html(url_st)
df_st = l_st[0].T.iloc[:,117:]
s_st = df_st.iloc[9:13,0]
for i in range(1,15):
  s_st = pd.concat([s_st,df_st.iloc[1:13,i]])
s_st = pd.concat([s_st,df_st.iloc[1:7,15]])
df['sunshine time'] = s_st.astype(str).str.replace(')','',regex=True).values.astype(np.float64)

# 降水量(rain)
url_ra = 'https://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s3.php?prec_no=44&block_no=47662&year=&month=&day=&view=p5'
l_ra = pd.read_html(url_ra)
df_ra = l_ra[0].T.iloc[:,132:]
s_ra=df_ra.iloc[9:13,0]
for i in range(1,15):
  s_ra = pd.concat([s_ra,df_ra.iloc[1:13,i]])
s_ra = pd.concat([s_ra,df_ra.iloc[1:7,15]])
df['rain']= s_ra.values.astype(np.float64)

df.head()

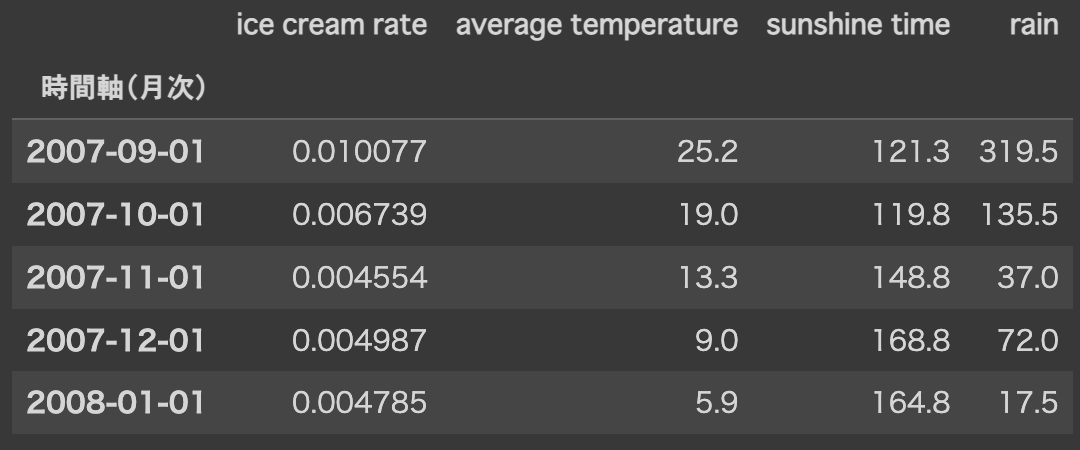
これで4つの特徴量を時系列データとして、1つのデータセットにまとめることが出来ました！

3. 統計量の表示

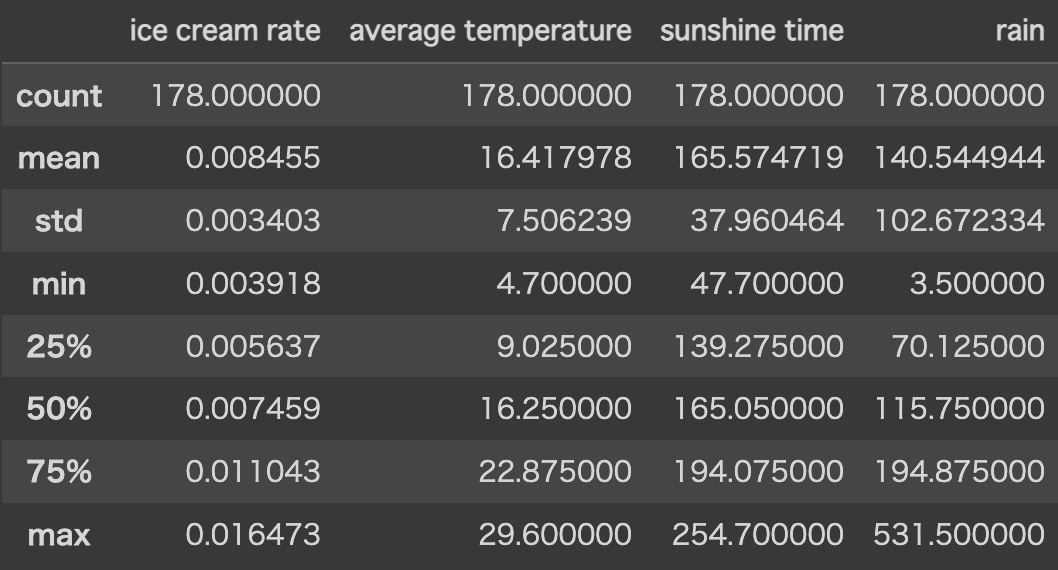
データに欠損値やエラー値がないことを確認しておきます。

display(df_ym.describe())

大丈夫そうです。

4. マルチインデックスの設定

”年"や"月"でカテゴリー化して集計できるようにマルチインデックスを設定します。

df_ym = df.set_index([df.index.year, df.index.month, df.index])
df_ym.index.names = ['year', 'month', 'date']

df_ym.head()

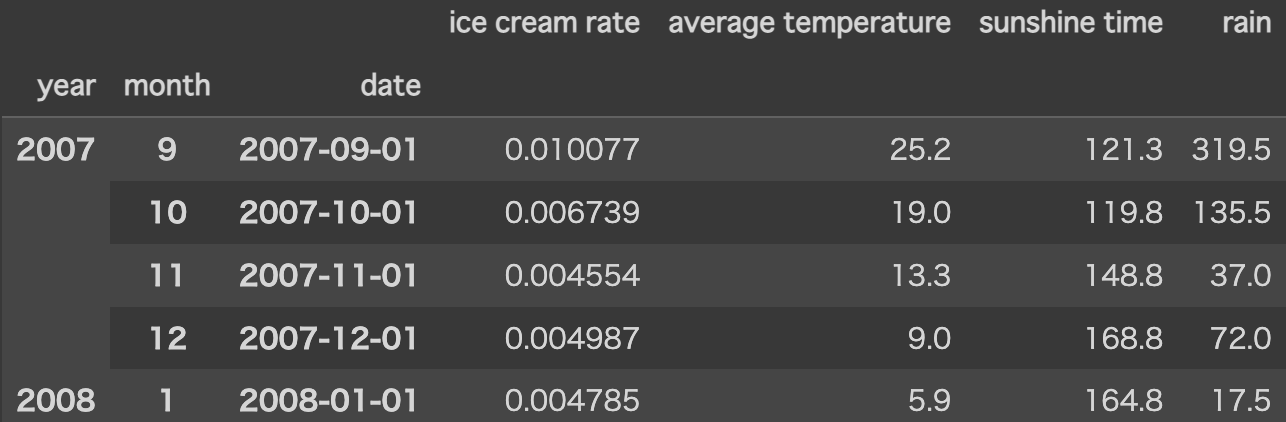
マルチインデックスを設定することで、特定の"年"や"月”のデータを抽出することが容易になります。
次節で、実際にデータ全体から8月のデータを抽出しています。

5. ヒートマップの作成

データ全体から8月のデータを抽出し、各特徴量の相関度合を可視化してみます。

# 8月のデータを抽出
df_aug = df_ym.groupby(['month']).get_group((8))

# ヒートマップの作成
import seaborn as sns
import matplotlib.pyplot as plt

sns.heatmap(
    df_aug[['ice cream rate','average temperature','sunshine time','rain']].corr(),
    vmax=1,vmin=-1,annot=True
    )

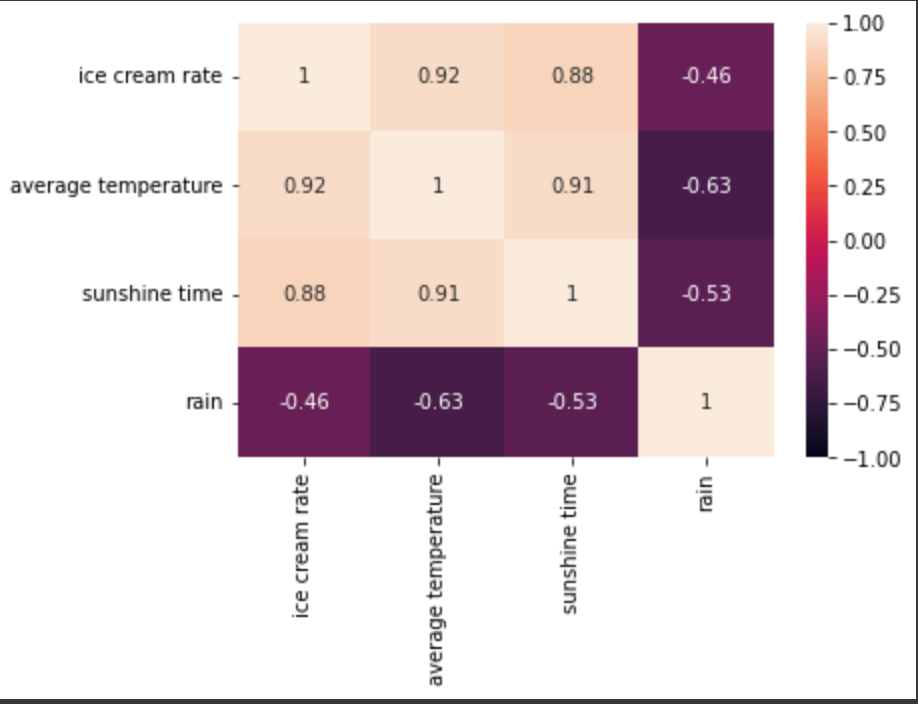
アイスクリームの消費量(ice cream rate)と、平均気温(average temperture)や日照時間(sunshine time)との間には強い正の相関、降水量(rain)との間には弱い負の相関が見られます。
同じ8月でも、暑くて昼の長さが長いとアイスクリームの消費量は増え、雨の日が多いとアイスクリームの消費量は減るようです（まあそうだろうな...）。

6. グラフを作成しデータを可視化

次にMatplotlibで折れ線グラフを描画してみます。前節で得られた相関度合いを視覚的に理解することが目的です。
まずアイスクリームの消費量(ice cream rate)と平均気温(average temperture)の2軸グラフにトライします。

import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import MaxNLocator
import matplotlib.ticker as ticker
# 図全体と座標軸の配置を決定します
fig = plt.figure(figsize=(10.0, 6.0))
ax1 = fig.add_subplot(1, 1, 1)
ax2 = ax1.twinx()
# x軸の目盛りを年刻みに設定します
ax1.set_xticks(df_aug.reset_index()["year"].values)
# データを生成します
x1 = df_aug.reset_index()["year"]
y1 = df_aug['ice cream rate']
y2 = df_aug['average temperature']
# y軸の目盛と目盛ラベルの色を指定します
color_1 = cm.Set1.colors[1]
color_2 = cm.Set1.colors[0]
ax1.tick_params(axis='y', colors=color_1)
ax2.tick_params(axis='y', colors=color_2)
# y軸の色を指定します
ax2.spines['left'].set_color(color_1)
ax2.spines['right'].set_color(color_2)
# 片方のy軸の目盛りの表記法を「○℃」の形式に指定します
ax2.yaxis.set_major_formatter(ticker.FormatStrFormatter('%d℃'))
# 片方のy軸の範囲を設定します
ax2.set_ylim([0, 1.1 * max(y2)])
# グラフタイトルを指定します
plt.title('blue = ice cream rate / red = average temperature', fontsize=15)
# データをプロットします
ax1.plot(x1, y1, label = 'ice cream rate', color = color_1)
ax2.plot(x1, y2, label = 'average temperature', color = color_2)

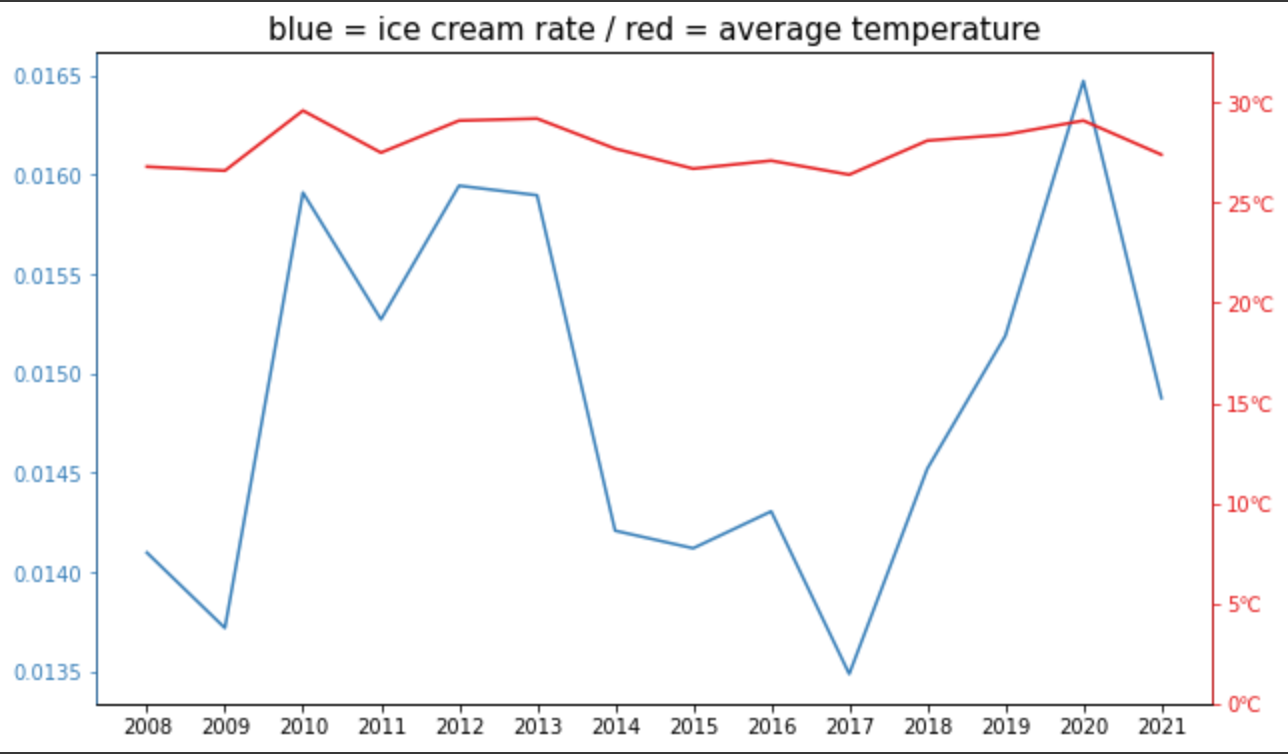
2つの折れ線グラフは毎年8月のアイスクリームの消費量と平均気温の推移を表しています。
しかし、2つの折れ線グラフの単位が異なるため、相関度合いがイマイチ掴みにくいです。
ここで元のデータに対し、標準化(平均が0、標準偏差が1となるように値を置き換える)という処理を行います。

7. 標準化

scikit-learnのモジュールを使って、データ全体に対し標準化を施します。

from sklearn.preprocessing import StandardScaler

# インスタンス (平均=0, 標準偏差=1)
standard_sc = StandardScaler()
# 値を変換します
X = df_ym.iloc[:, :]
X = standard_sc.fit_transform(X)
# 変換した値でデータを書き換えます
df_ym_std = df_ym.copy()
df_ym_std.iloc[:, :] = X
# 8月のデータを抽出します
df_aug_std = df_ym_std.groupby(['month']).get_group((8))

df_aug_std.head()

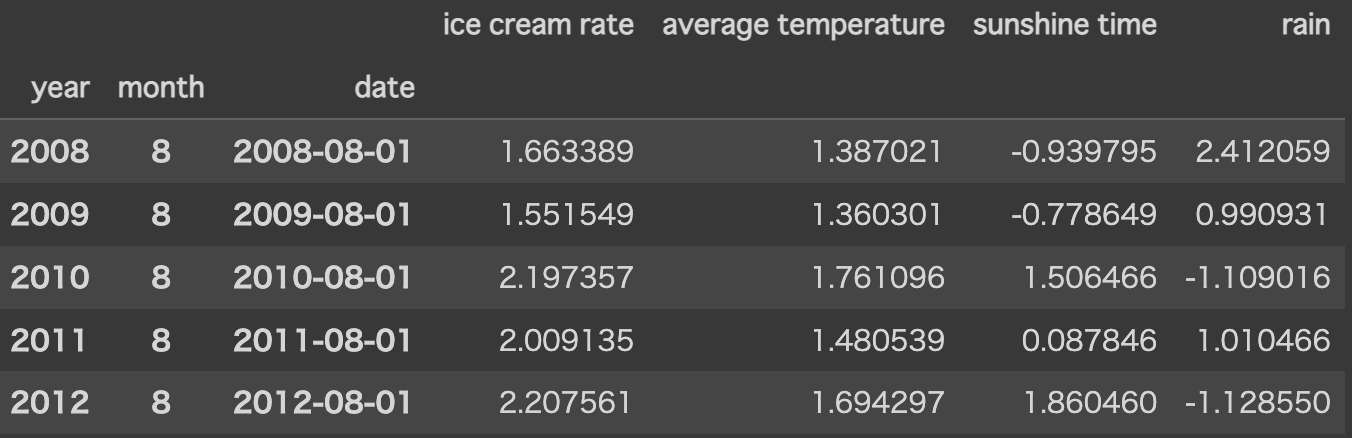
無事データを標準化することができました。
こちらを前節と同じ手順でグラフ化します。

fig2 = plt.figure(figsize=(10.0, 6.0))
ax3 = fig2.add_subplot(1, 1, 1)
ax4 = ax3.twinx()
ax3.set_xticks(df_aug_std.reset_index()["year"].values)
x2 = df_aug_std.reset_index()["year"]
y3 = df_aug_std['ice cream rate']
y4 = df_aug_std['average temperature']
ax3.tick_params(axis='y', colors=color_1)
ax4.tick_params(axis='y', colors=color_2)
ax3.spines['left'].set_color(color_1)
ax4.spines['right'].set_color(color_2)
plt.title('blue = ice cream rate(SD) / red = average temperature(SD)', fontsize=15)
ax3.plot(x2, y3, label = 'ice cream rate', color = color_1)
ax4.plot(x2, y4, label = 'average temperature', color = color_2)

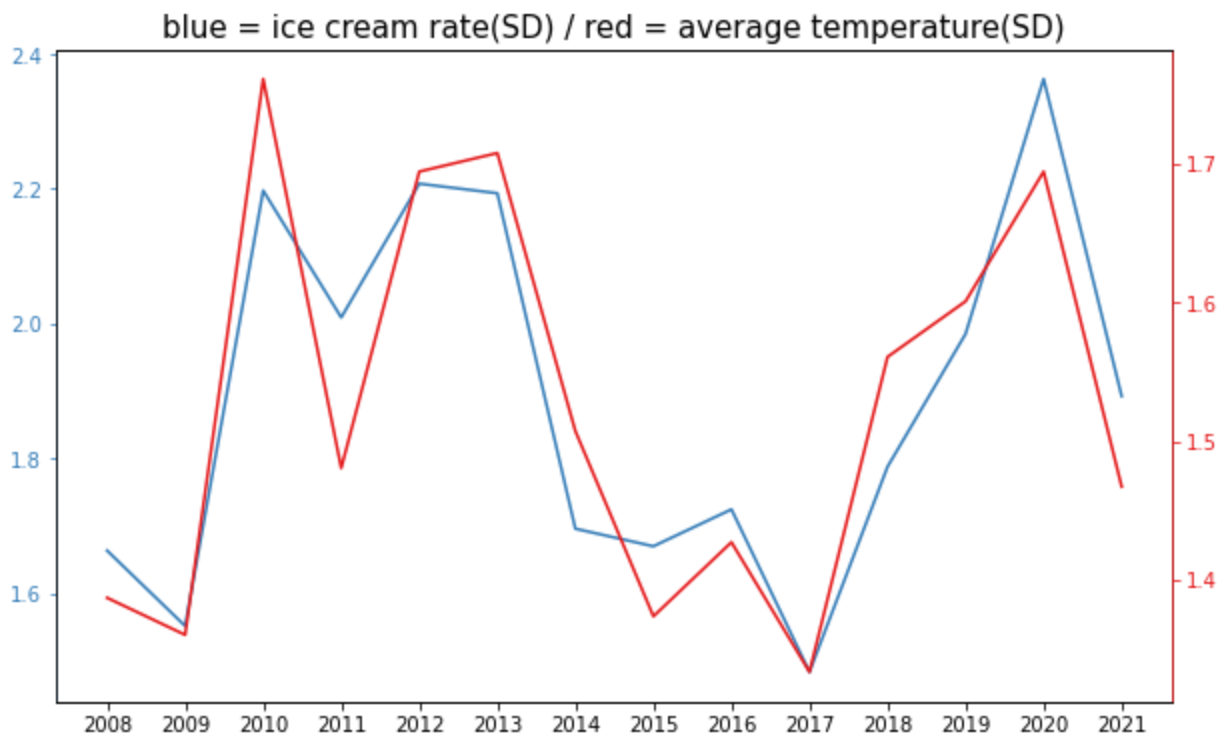
先程と同じく毎年8月のアイスクリームの消費量と平均気温の推移を表していますが、標準化を行うことで2本の折れ線グラフが連動している様子（相関度合い）がより分かりやすくなりました。
それでは日照時間(sunshine time)と降水量(rain)についても、同様にグラフ化してみます。
まず日照時間(sunshine time)をプロットします。

# 日照時間(sunshine time)のプロット
fig3 = plt.figure(figsize=(10.0, 6.0))
ax5 = fig3.add_subplot(1, 1, 1)
ax6 = ax5.twinx()
ax5.set_xticks(df_aug_std.reset_index()["year"].values)
y5 = df_aug_std['sunshine time']
ax5.tick_params(axis='y', colors=color_1)
ax6.tick_params(axis='y', colors=color_2)
ax5.spines['left'].set_color(color_1)
ax6.spines['right'].set_color(color_2)
plt.title('blue = ice cream rate(SD) / red = sunshine time(SD)', fontsize=15)
ax5.plot(x2, y3, label = 'ice cream rate', color = color_1)
ax6.plot(x2, y5, label = 'sunshine time', color = color_2)

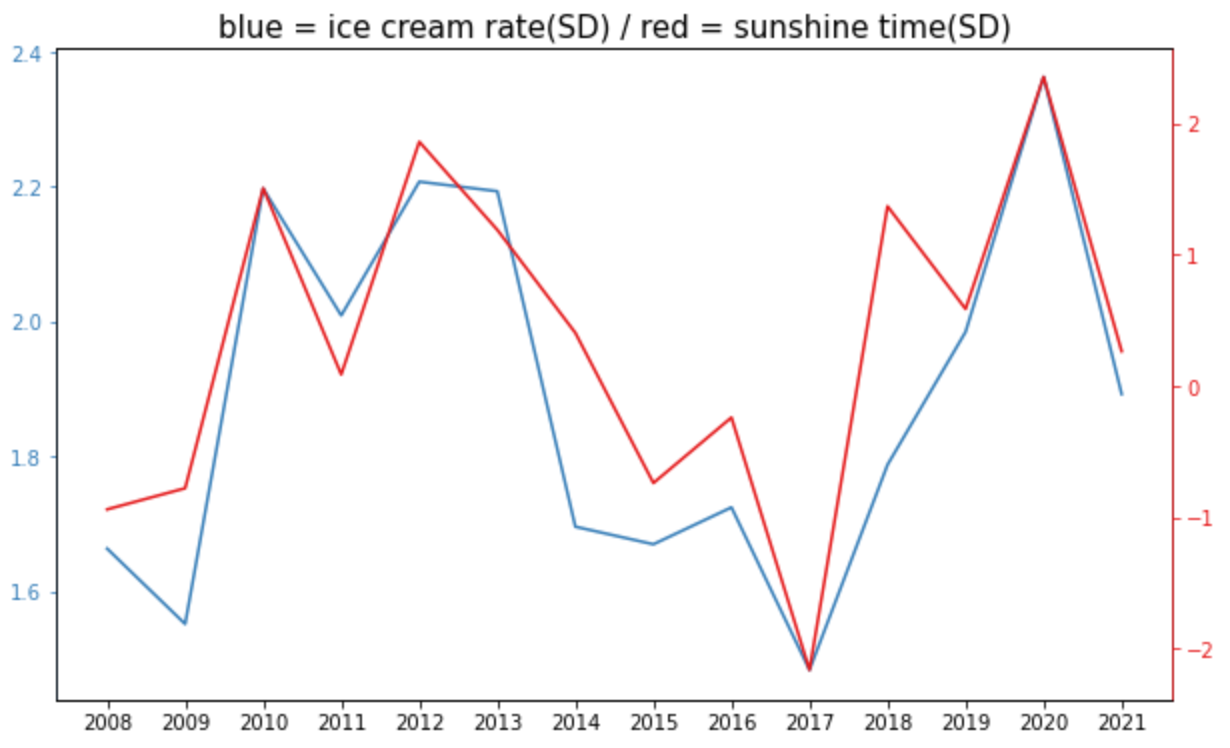
毎年8月のアイスクリームの消費量と日照時間の推移を表すグラフが描けました。
ヒートマップの数値(相関係数:0.88)の通り、2本の折れ線グラフの動きはよく似ています。

次に降水量(rain)をプロットします。

# 降水量(`rain`)のプロット
fig4 = plt.figure(figsize=(10.0, 6.0))
ax7 = fig4.add_subplot(1, 1, 1)
ax8 = ax7.twinx()
ax7.set_xticks(df_aug_std.reset_index()["year"].values)
y6 = df_aug_std['rain']
ax7.tick_params(axis='y', colors=color_1)
ax8.tick_params(axis='y', colors=color_2)
ax7.spines['left'].set_color(color_1)
ax8.spines['right'].set_color(color_2)
plt.title('blue = ice cream rate(SD) / red = rain(SD)', fontsize=15)
ax7.plot(x2, y3, label = 'ice cream rate', color = color_1)
ax8.plot(x2, y6, label = 'rain', color = color_2)

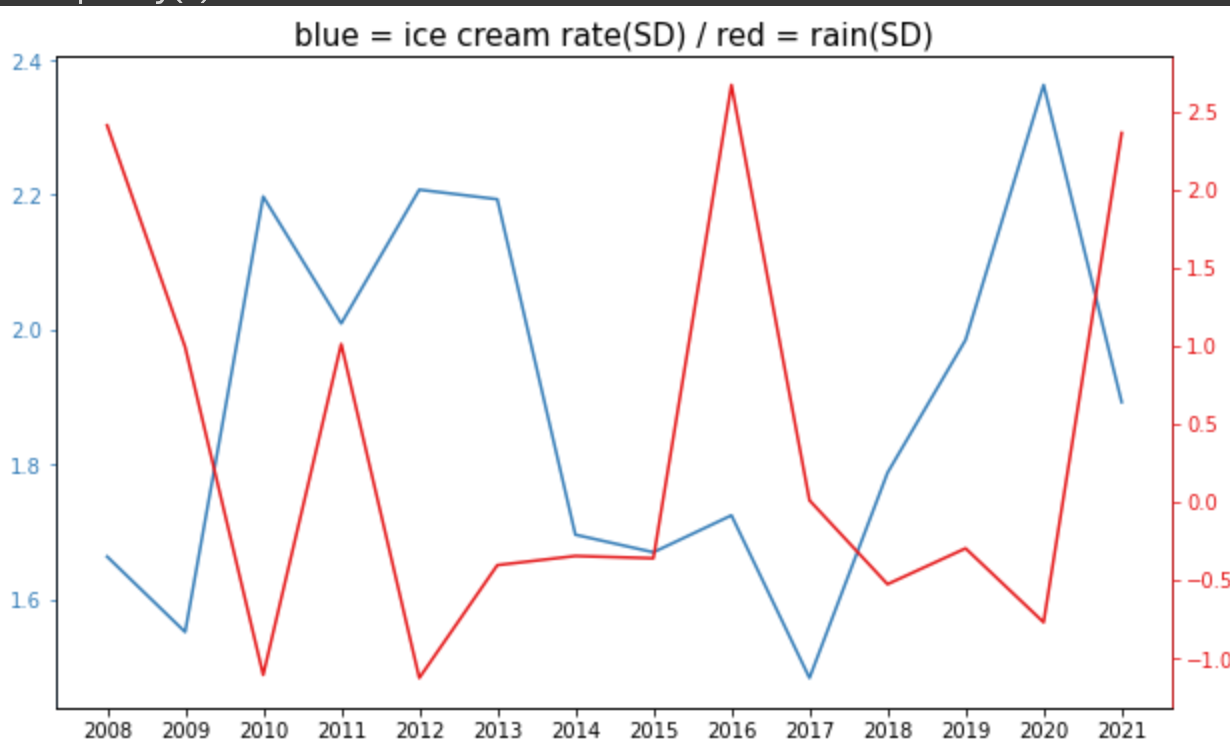
毎年8月のアイスクリームの消費量と降水量の推移です。
相関係数（-0.46）が示す通り、概して2本のグラフが逆の動きをしているように見えます。

8. モデル構築

最後にscikit-learnライブラリのLinearRegressionメソッドを用いて線形回帰モデルの構築・検証を行います。
ここからはデータ全体(全期間)を扱います。

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# 説明変数X：平均気温、日照時間、降水量｜目的変数y：アイスクリームの消費量
X = df_ym_std.iloc[:, 1:4]
y = df_ym_std.iloc[:, 0]
# 訓練データ:テストデータ=8:2に分割します
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, shuffle=False)
# 訓練データをモデルに学習させます
model = LinearRegression()
model.fit(X_train, y_train)
# 決定係数を計測します
print(model.score(X_test, y_test))

決定係数は「線形モデルがどの程度目的変数を説明できるか」を表しています。
０から１の間の値をとり、分析精度が高いほど数値は大きくなります。
今回は「まずまず」の結果と言えそうです。

実際に予測値が観測データ（正解データ）にどの程度フィットしているか、こちらもグラフで確認してみます。

# 目的変数：アイスクリームの消費量を学習させます
standard_sc.fit(df_ym.iloc[:, 0].values.reshape(-1, 1))
# テストデータとして用いた期間について元の値を予測値で置き換えたデータを生成します
df_ym_lr = df_ym.copy()
df_ym_lr.iloc[len(X_train):, 0] = 
standard_sc.inverse_transform(model.predict(X_test).reshape(-1, 1)) # model.predict(X_test)は標準偏差を返すため、元の単位に逆変換する必要があります

# 図を描画します
plt.figure(figsize=(10,6))
# x軸の表示範囲を対象期間に限定します
plt.xlim(df_ym.reset_index()["date"][len(X_train)-1], df_ym.reset_index()["date"][len(df_ym)-1])
# プロットします
plt.plot(df_ym.reset_index()["date"], df_ym['ice cream rate'], label='original')
plt.plot(df_ym_lr.reset_index()["date"], df_ym_lr['ice cream rate'], '--', label='predict')
# 凡例の位置を指定します
plt.legend(loc='upper left')

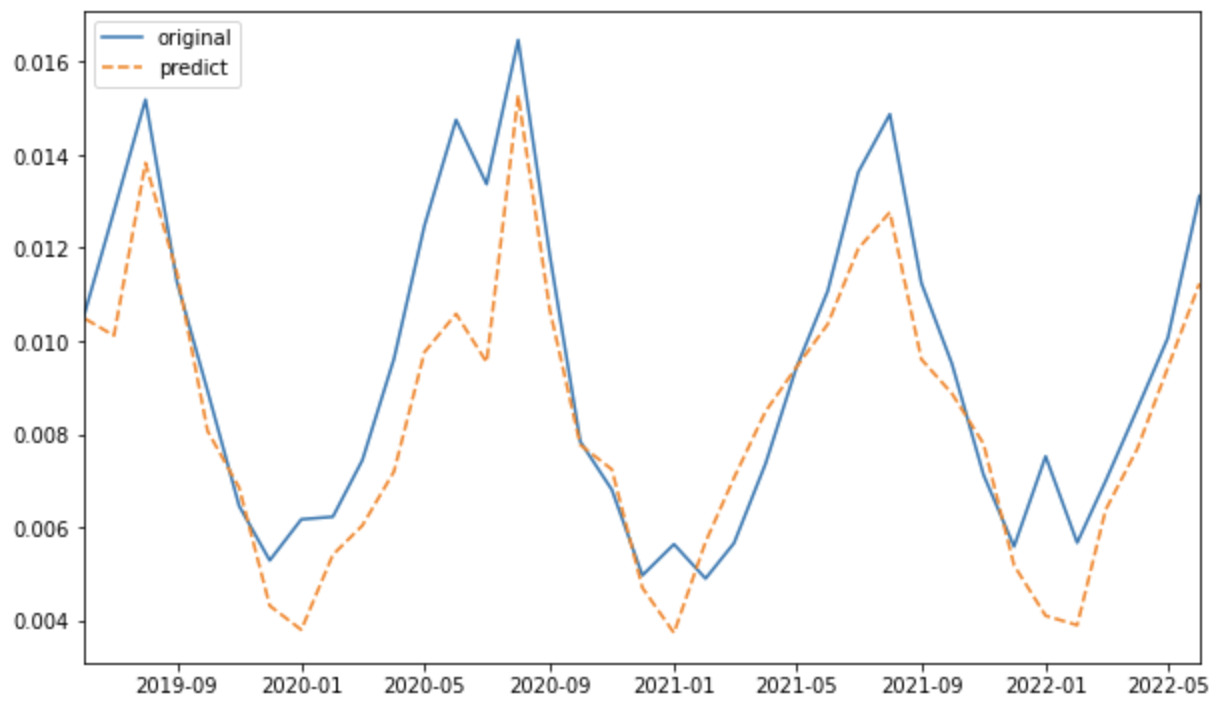
グラフ全体を通して、予測データ（predict）は観測データ（original)に近い動きをしています。
予測に用いたのは気象データのみですが、アイスクリームの消費量のトレンドをまずまず表現できたと言えるのではないでしょうか。

一方で、周期の谷になっている各年の1月では予測データ（predict）と観測データ（original)の乖離が大きくなる傾向が見て取れます。
これについては今回の検証が、アイスクリームの消費量における季節変動を考慮できていないことが原因の一つと考えられます。
今回のモデルは気象データの特徴（平均気温が低いこと等）から、毎年1月のアイスクリームの消費量をかなり低く予測しましたが、実際は年末年始の各種のイベントでアイスクリームが提供されるため（？）²、毎年1月の消費量は極端に落ち込みまないということでしょう。

以上の通り、まだまだ修正する余地しかありませんが、本記事では検証はここまでにしたいと思います。

9. 所見

• 支離滅裂な展開ですみません（恣意的に8月のみを抽出して特徴量間の相関度合いを検証したり、かと思えば全期間でモデルの構築を始めたり・・・）。
• 本来今回のようなケースではSARIMAXというモデルを使うことで、季節変動性を持つデータに外生変数（今回でいう気象データ）を組み込んだモデル化ができるようです。
• あと説明変数同士に相関（今回では平均気温と日照時間との間の強い正の相関、平均気温と降水量との間の負の相関）があるのも、本来は良くありません。このような現象を線形従属と呼び、正則化・次元削減といった対策をする必要があります。
• それぞれの機械学習モデルの特徴や用途について、まだまだ勉強する必要を感じています。
• 上記等々、課題はたくさんですが、それでも今回自分でコードを書いてみて学習した内容を再確認できましたし、理解が進んだとも感じました。
• モデル化の前準備（DataFrameの整理・型の統一など）の大変さも少し味わえて、いい経験になったと思っています。
• 最後になりますがAidemyの講師陣の皆様、カリキュラムでも今回の成果物でも、いつも適時適切なサポートを頂き大変ありがとうございました。学習は総じて楽しかったですし、これからも勉強を継続したいと感じています！

1. 正確にはシャーベットも含まれます ↩

2. 著者の勝手な憶測です。 ↩