2024東大理系数学第3問
連立漸化式を行列表示する
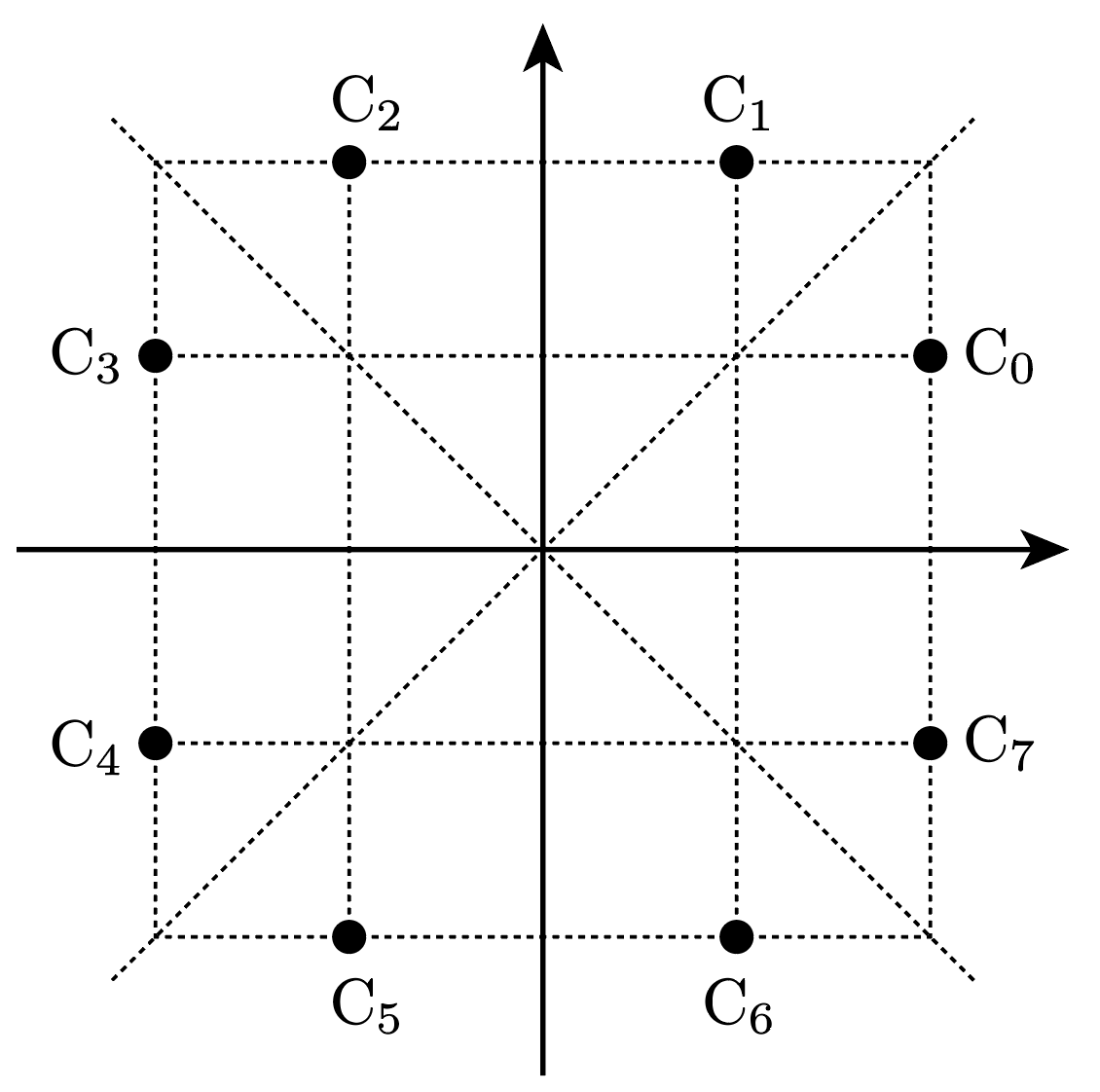
(1)で答える,とりうる点を反時計回りに点$\mathrm{C}_0, \mathrm{C}_1, \ldots, \mathrm{C}_7$とおきます。
そして,$n$秒後に点$\mathrm{P}$ が $C_k$ にいる確率を $p_{n,k}$ とおくと,$n$秒後から$n+1$秒後への推移は次の行列で表されます。
\begin{pmatrix}
p_{n+1,0}\\
p_{n+1,1}\\
p_{n+1,2}\\
p_{n+1,3}\\
p_{n+1,4}\\
p_{n+1,5}\\
p_{n+1,6}\\
p_{n+1,7}
\end{pmatrix}
=\frac{1}{6}
\left(
\begin{array}{cccccccc}
0 & 1 & 0 & 2 & 0 & 1 & 0 & 2 \\
1 & 0 & 2 & 0 & 1 & 0 & 2 & 0 \\
0 & 2 & 0 & 1 & 0 & 2 & 0 & 1 \\
2 & 0 & 1 & 0 & 2 & 0 & 1 & 0 \\
0 & 1 & 0 & 2 & 0 & 1 & 0 & 2 \\
1 & 0 & 2 & 0 & 1 & 0 & 2 & 0 \\
0 & 2 & 0 & 1 & 0 & 2 & 0 & 1 \\
2 & 0 & 1 & 0 & 2 & 0 & 1 & 0 \\
\end{array}
\right)
\begin{pmatrix}
p_{n,0}\\
p_{n,1}\\
p_{n,2}\\
p_{n,3}\\
p_{n,4}\\
p_{n,5}\\
p_{n,6}\\
p_{n,7}
\end{pmatrix}
この8次正方行列部分を$A$とおき,
\boldsymbol{v}_n = \begin{pmatrix}p_{n,0}\\\vdots\\p_{n,7}\end{pmatrix}
とおけば,推移は
\boldsymbol{v}_{n+1} = \frac{1}{6} A\boldsymbol{v}_{n}
と表せることになります。ただし,はじめ点$\mathrm{C}_0$にいることから,
\boldsymbol{v}_0 = \begin{pmatrix}1\\0\\\vdots\\0\end{pmatrix}
となります。
よって,$n$秒後の確率分布は
\boldsymbol{v}_{n} = \frac{1}{6^n} A^n \boldsymbol{v}_{0}
と表せるので,行列の累乗 $A^n$ を求めることが目標となります。
sympy の環境準備
ブラウザ上で Python, sympy の環境を気軽に試せ,数式の見た目も MathJax で綺麗に表示される Juypter Notebook で Notebook を作って実験してみましょう。
新規 Notebook を作成したら,まずは sympy の初期設定をします。
import sympy
sympy.init_printing()
init_printing() によって,結果を MathJax によって綺麗な数式として表示できるようになります。
次の関数も便利です。
-
display(hoge):hogeを MathJax によって綺麗に表示 -
print(sympy.latex(hoge)):hogeを LaTeX ソースとして表示
行列Aの定義
まずは行列$A$を定義します。
input
A = sympy.Matrix([
[0, 1, 0, 2, 0, 1, 0, 2],
[1, 0, 2, 0, 1, 0, 2, 0],
[0, 2, 0, 1, 0, 2, 0, 1],
[2, 0, 1, 0, 2, 0, 1, 0],
[0, 1, 0, 2, 0, 1, 0, 2],
[1, 0, 2, 0, 1, 0, 2, 0],
[0, 2, 0, 1, 0, 2, 0, 1],
[2, 0, 1, 0, 2, 0, 1, 0]
])
display(A)
output
\left[
\begin{array}{cccccccc}
0 & 1 & 0 & 2 & 0 & 1 & 0 & 2 \\
1 & 0 & 2 & 0 & 1 & 0 & 2 & 0 \\
0 & 2 & 0 & 1 & 0 & 2 & 0 & 1 \\
2 & 0 & 1 & 0 & 2 & 0 & 1 & 0 \\
0 & 1 & 0 & 2 & 0 & 1 & 0 & 2 \\
1 & 0 & 2 & 0 & 1 & 0 & 2 & 0 \\
0 & 2 & 0 & 1 & 0 & 2 & 0 & 1 \\
2 & 0 & 1 & 0 & 2 & 0 & 1 & 0 \\
\end{array}
\right]
対角化可能性の確認
まずは行列$A$の固有値を求めてみます。
input
A.eigenvals()
output
\left\{ -6 : 1, -2 : 1, 0 : 4, 2 : 1, 6 : 1\right\}
このそれぞれは,固有値:代数的重複度 を表します。固有値0の重複度が高いので,固有空間の次元を確認しておきましょう。
input
A.eigenvects()
output
\displaystyle \left[ \left( -6, \ 1, \ \left[ \left[\begin{matrix}-1\\1\\-1\\1\\-1\\1\\-1\\1\end{matrix}\right]\right]\right), \ \left( -2, \ 1, \ \left[ \left[\begin{matrix}-1\\-1\\1\\1\\-1\\-1\\1\\1\end{matrix}\right]\right]\right), \ \left( 0, \ 4, \ \left[ \left[\begin{matrix}-1\\0\\0\\0\\1\\0\\0\\0\end{matrix}\right], \ \left[\begin{matrix}0\\-1\\0\\0\\0\\1\\0\\0\end{matrix}\right], \ \left[\begin{matrix}0\\0\\-1\\0\\0\\0\\1\\0\end{matrix}\right], \ \left[\begin{matrix}0\\0\\0\\-1\\0\\0\\0\\1\end{matrix}\right]\right]\right), \ \left( 2, \ 1, \ \left[ \left[\begin{matrix}1\\-1\\-1\\1\\1\\-1\\-1\\1\end{matrix}\right]\right]\right), \ \left( 6, \ 1, \ \left[ \left[\begin{matrix}1\\1\\1\\1\\1\\1\\1\\1\end{matrix}\right]\right]\right)\right]
このそれぞれは,(固有値,代数的重複度,その固有値に属する固有空間の基底) を表します。固有値0に属する固有空間の次元が4となっていることから,固有空間の次元の総和が8になり,$A$が対角化可能な行列であることが分かります。また,$\dim\mathop{\mathrm{Ker}}A=4$となることから,一般に$m\times n$次行列$A$に対して成り立つ次元定理
\dim\mathop{\mathrm{Ker}}A + \mathop{\mathrm{rank}} A = n
により,$A$の階数が4 (A.rank() == 4)であることが分かり,直観的には「独立な変数が4変数しかない」ことが分かります。これは,元の問題の(2)の誘導で気づかせようとしている対称性に対応しています。
対角化実行
対角化を実行します。(既に上で固有ベクトルを全て見つけてはいますが)$D=P^{-1}AP$ なる正則行列$P$と対角行列$D$を次のようにして見つけます。
P, D = A.diagonalize()
それぞれの行列を成分表示してみます。
input
display(P, D)
output
\displaystyle \left[\begin{matrix}-1 & -1 & -1 & 0 & 0 & 0 & 1 & 1\\1 & -1 & 0 & -1 & 0 & 0 & -1 & 1\\-1 & 1 & 0 & 0 & -1 & 0 & -1 & 1\\1 & 1 & 0 & 0 & 0 & -1 & 1 & 1\\-1 & -1 & 1 & 0 & 0 & 0 & 1 & 1\\1 & -1 & 0 & 1 & 0 & 0 & -1 & 1\\-1 & 1 & 0 & 0 & 1 & 0 & -1 & 1\\1 & 1 & 0 & 0 & 0 & 1 & 1 & 1\end{matrix}\right]
\displaystyle \left[\begin{matrix}-6 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & -2 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 2 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 6\end{matrix}\right]
念のため,本当にこれで対角化できているか確認します。
P.inv()*A*P == D # => True
n乗計算
$n$を正の整数の変数扱いします。
n = sympy.Symbol('n', integer=True, positive=True)
すると,対角行列 $D$ の $n$ 乗はこのように正しく計算されます。
input
display(D**n)
output
\displaystyle \left[\begin{matrix}\left(-6\right)^{n} & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & \left(-2\right)^{n} & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 2^{n} & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 6^{n}\end{matrix}\right]
こうして,$A^n=PD^nP^{-1}$ が次のように計算できます。
input
display(P*(D**n)*P.inv())
output
\displaystyle \left[\begin{matrix}\frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\\\frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\\- \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\\- \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\\\frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\\\frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\\- \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\\- \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8} & - \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8} & \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\end{matrix}\right]
これにより,
\boldsymbol{v}_{n} = \frac{1}{6^n} A^n \boldsymbol{v}_{0}
は次のように計算できます。
input
B = P*(D**n)*P.inv()/(6**n) # A^nをBとおく
v = sympy.Matrix([1,0,0,0,0,0,0,0]) # 初期値v_0
p = B*v # n秒後の確率分布
display(p)
output
\displaystyle \left[\begin{matrix}6^{- n} \left(\frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(\frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(- \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(- \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(\frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(\frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(- \frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} - \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\6^{- n} \left(- \frac{\left(-2\right)^{n}}{8} - \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\end{matrix}\right]
設問に答える
(2)
上の p[0] と p[4] はともに $6^{- n} \left(\frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)$ であり,確かに等しいことが分かります。
p[0] == p[4] # => True
(3)
上の p[0] が求めるべき $p_{n,0}$ です。
\begin{align*}
p_{n,0} &= 6^{- n} \left(\frac{\left(-2\right)^{n}}{8} + \frac{\left(-6\right)^{n}}{8} + \frac{2^{n}}{8} + \frac{6^{n}}{8}\right)\\
&=\begin{cases}
0 & (n:奇数)\\
\frac{1}{4}\left(1+\frac{1}{3^n}\right)& (n:偶数)
\end{cases}
\end{align*}