JuliaでDeep Learningを理解する: 2.1 Supervised Learning

Understanding Deep LearningのノートブックをJuliaで確認する。

2.1 Supervised Learning

あるxに対して観測値yが得られているとする。

x = [0.03, 0.19, 0.34, 0.46, 0.78, 0.81, 1.08, 1.18, 1.39, 1.60, 1.65, 1.90]
y = [0.67, 0.85, 1.05, 1.0, 1.40, 1.5, 1.3, 1.54, 1.55, 1.68, 1.73, 1.6]

xとyの関係を表すモデルをyを用いて訓練することを教師あり学習という。

線形回帰モデル

xとyをプロットする。

using CairoMakie
fig, ax, _ = scatter(x, y)

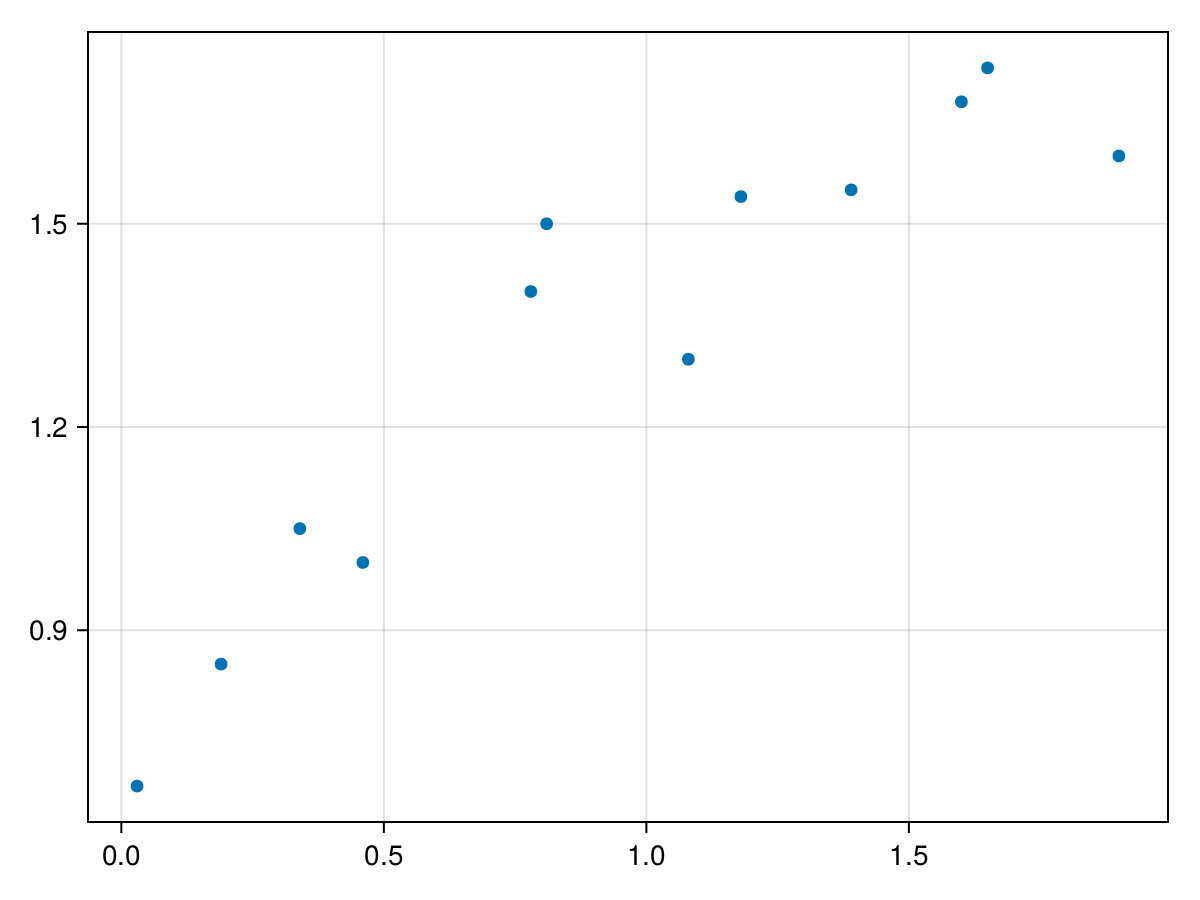
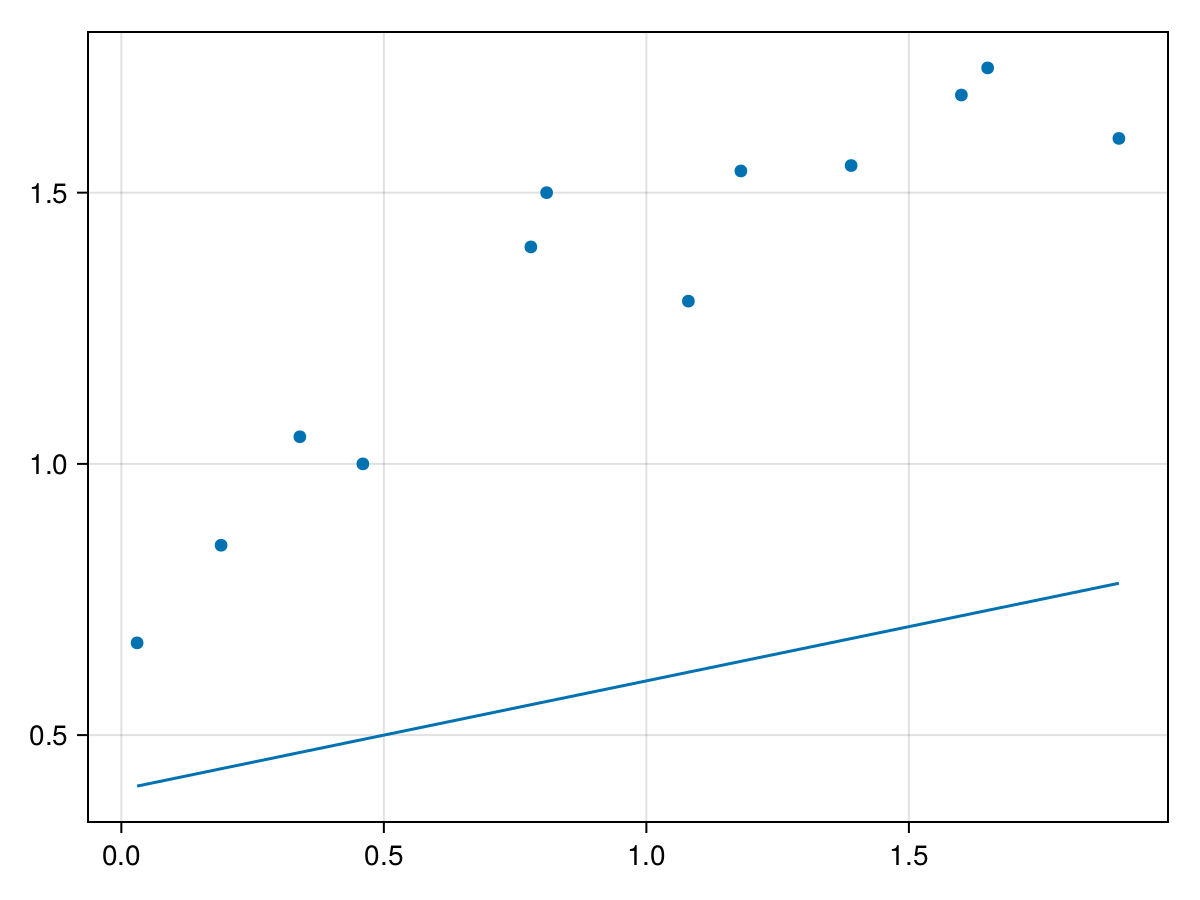
直線関係で近似できそうなので、線形回帰モデルで教師付き学習を行う。1次元線形回帰モデルを式で表すと

y = f[x, \phi] = \phi_0 + \phi_1 x

となる。Juliaで表すと

f(x, phi0, phi1) = phi0 + phi1 * x

である。取り敢えず$\phi_0=0.4, \ \phi_1=0.2$と固定する。

phi0, phi1 = 0.4, 0.2
lines!(ax, x, f.(x, phi0, phi1))

$\phi_0$は切片で$\phi_1$は傾きである。

損失関数

画像を見た感じ$y = 0.4 + 0.2 x$はxとyの関係を正しく表しているモデルとは言えない。正しさを数値にするために損失関数を定義する。

L[\phi] = \sum_{i=1}^{I} (f[x_i, \phi] - y_i)^2 = \sum_{i=1}^{I} (\phi_0 + \phi_1 x_i - y_i)^2

この損失関数は最小二乗損失である。モデルにxを入れて出てきた値$f[x_i, \phi]$から観測値$y_i$を引いて２乗した物を全ての点で足している。モデルが予想した値$f[x_i, \phi]$が教師である$y_i$に近ければ損失関数は小さくなる。つまり、モデルの正しさは損失関数の小ささで測ることができるようになった。

compute_loss(x, y, phi0, phi1) = sum((f.(x, phi0, phi1) .- y) .^ 2)
loss = compute_loss(x, y, phi0, phi1)

julia> loss
7.067864

φ0を求める

$\phi_0=0.4, \ \phi_1=0.2$の時、損失は7.067864である。$\phi_1=0.2$は固定し、$\phi_0$を色々変えて損失がどのように変化するか見てみる。

using Printf
phi0s = 0:0.2:2
fig = Figure()
ax1 = Axis(fig[1:2, 1])
scatter!(ax1, x, y)
lis = Lines[]
for (i, phi0) in phi0s |> enumerate
    v = i / length(phi0s)
    li = lines!(ax1, x, f.(x, phi0, phi1), color=RGBf(v, 0, 1 - v))
    push!(lis, li)
end
losses = compute_loss.(x |> Ref, y |> Ref, phi0s, phi1)
legends = [@sprintf "phi0=%.1f, loss=%.1f" phi0s[i] losses[i] for i in eachindex(phi0s)]
Legend(fig[1:2, 2], lis |> reverse, legends |> reverse)

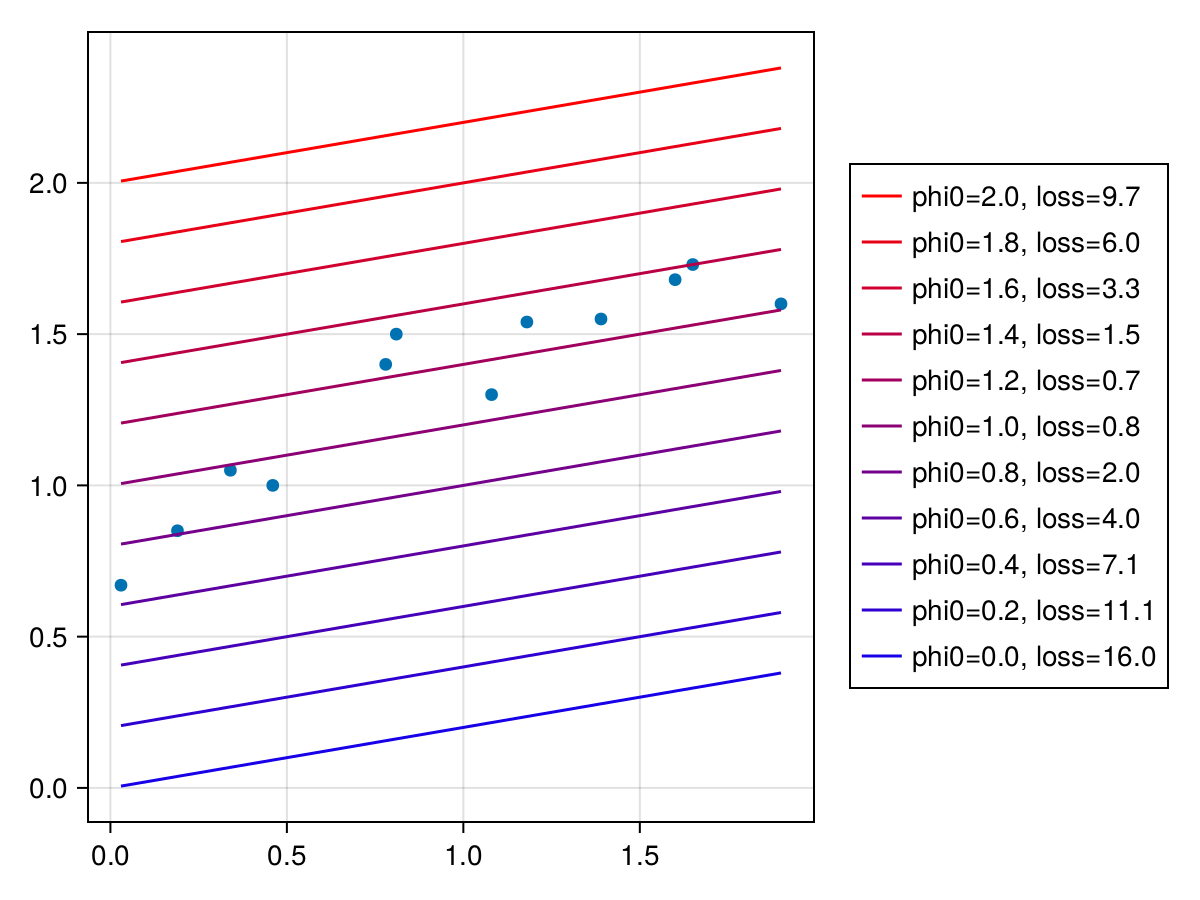
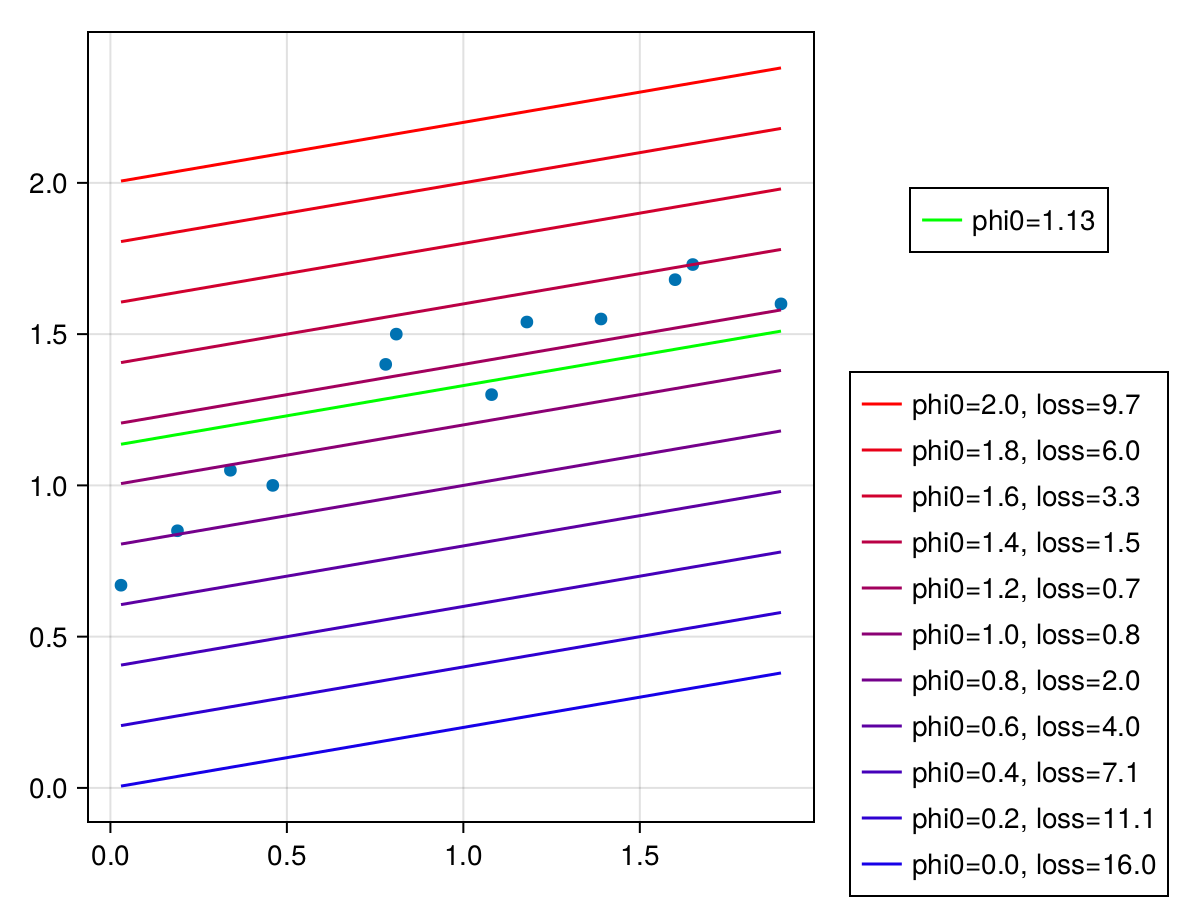
図から$\phi_0=1.2$のとき、損失が0.7で最も小さいことがわかる。より正確な値を求める。

phi0s = 1:0.01:1.4
minloss, minindex = findmin(compute_loss.(x |> Ref, y |> Ref, phi0s, phi1))
minphi0 = collect(phi0s)[minindex]

julia> minphi0,minloss
(1.13, 0.632184)

$\phi_0=1.13$の時、最小損失0.632184となるようだ。

φ1を求める

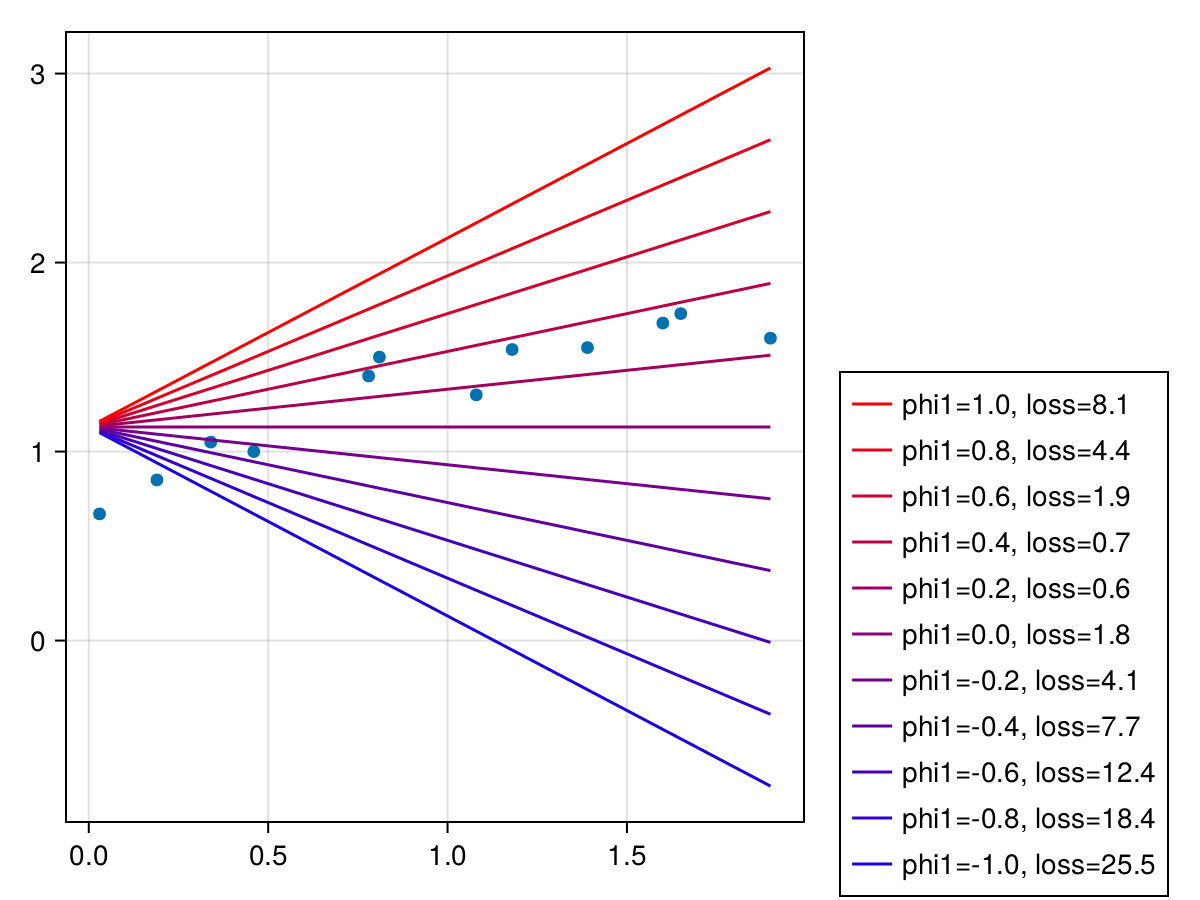
次は$\phi_0=1.13$を固定して、$\phi_1$を色々変えて損失がどのように変化するか見てみる。

phi1s = -1:0.2:1
fig = Figure()
ax1 = Axis(fig[1:2, 1])
scatter!(ax1, x, y)
lis = Lines[]
for (i, phi1) in phi1s |> enumerate
    v = i / length(phi1s)
    li = lines!(ax1, x, f.(x, minphi0, phi1), color=RGBf(v, 0, 1 - v))
    push!(lis, li)
end
losses = compute_loss.(x |> Ref, y |> Ref, minphi0, phi1s)
legends = [@sprintf "phi1=%.1f, loss=%.1f" phi1s[i] losses[i] for i in eachindex(phi1s)]
Legend(fig[2, 2], lis |> reverse, legends |> reverse)

phi1s = 0:0.01:0.4
minloss, minindex = findmin(compute_loss.(x |> Ref, y |> Ref, minphi0, phi1s))
minphi1 = collect(phi1s)[minindex]

julia> minphi1,minloss
(0.29, 0.5075276099999995)

$\phi_1=0.29$のとき、最小損失0.5075276となる。

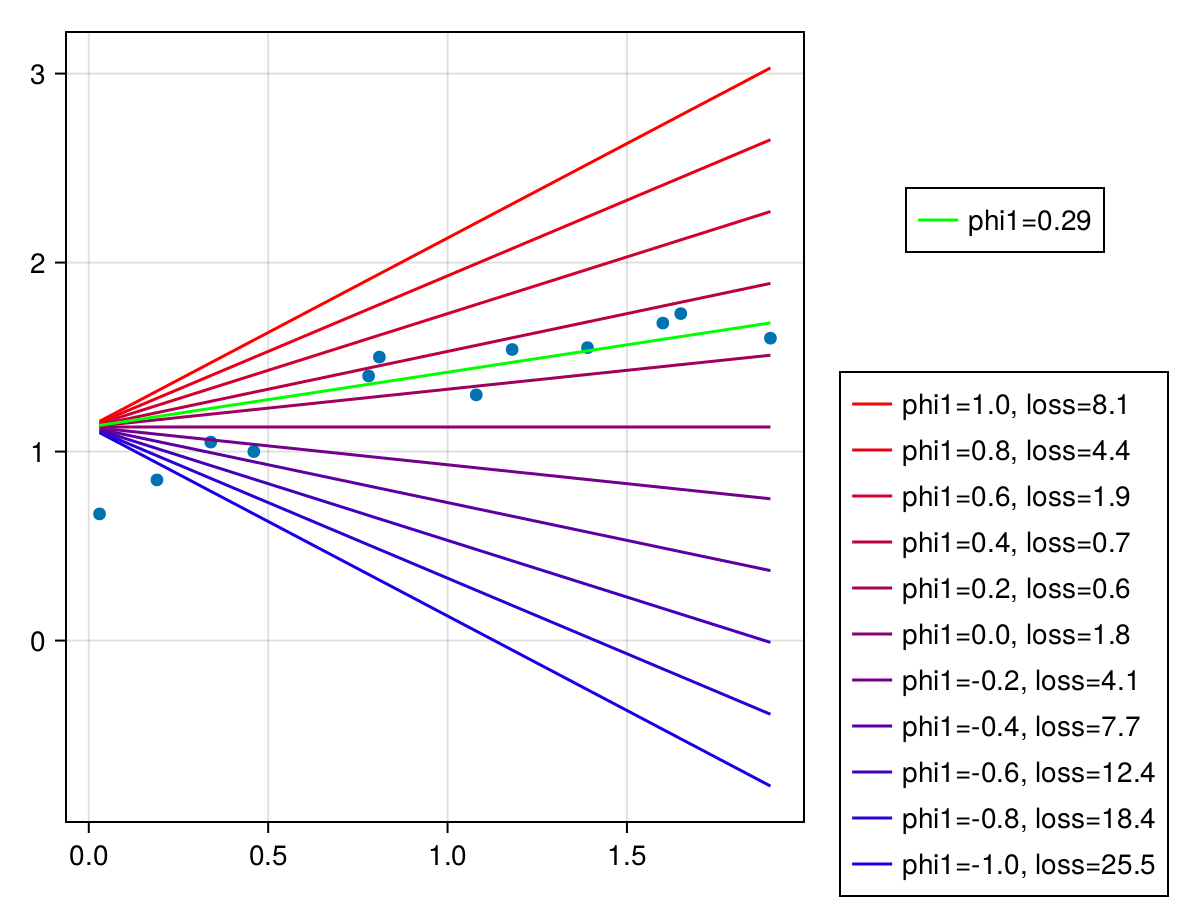
以上より1次元線形回帰モデルは$f[x, \phi] = 1.13 + 0.29 x$と求まった。今回、手作業で損失関数が最小となる$\phi$を探したが、これをどのように自動的に効率よく求めるかが問題となる。