はじめに
ある信号の周波数の時間変化を調べたい欲求がある人がいると思うが,そういうのを調べるのを時間周波数解析と言う.
時間周波数解析の基本として,今回は周波数の時間変化について解説し,代表的な周波数変調信号である線形チャープ信号や,任意の数式の周波数変調信号を作成し,matlabで確認してみることにする.
周波数が一定の信号を考える
周波数が時間変化する信号を考える前に,周波数が時間変化しない信号を考える.
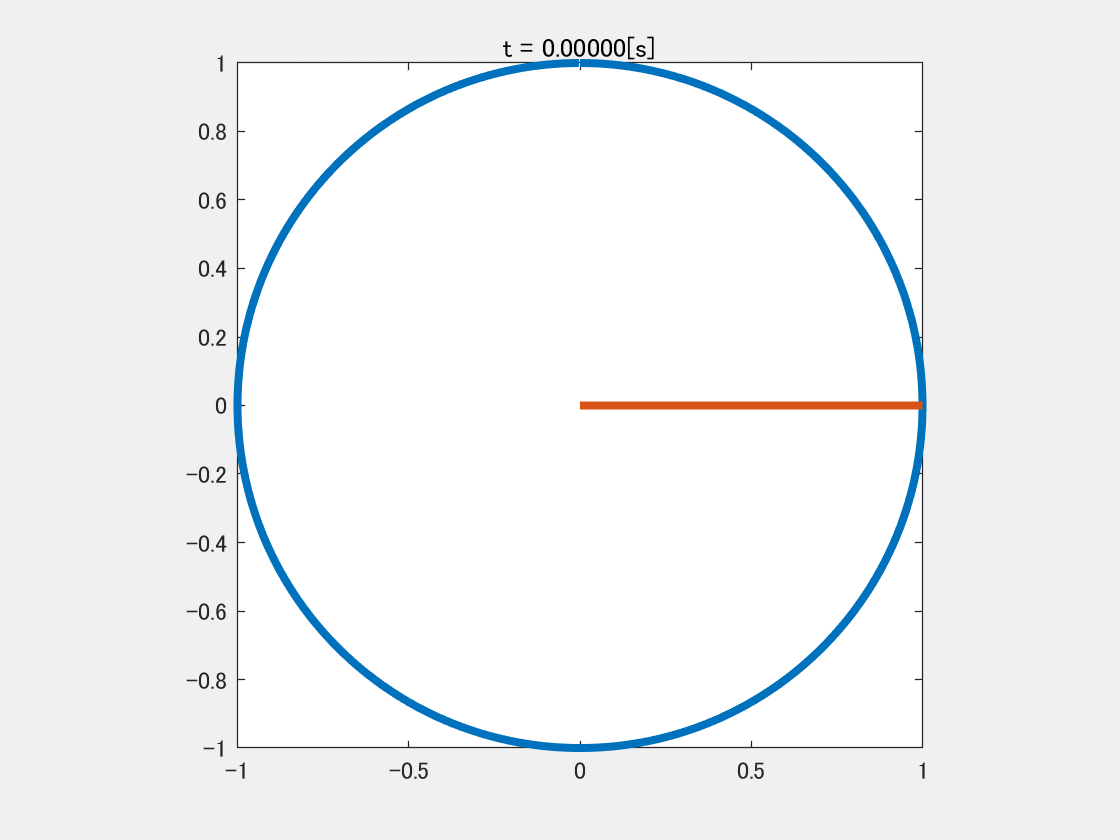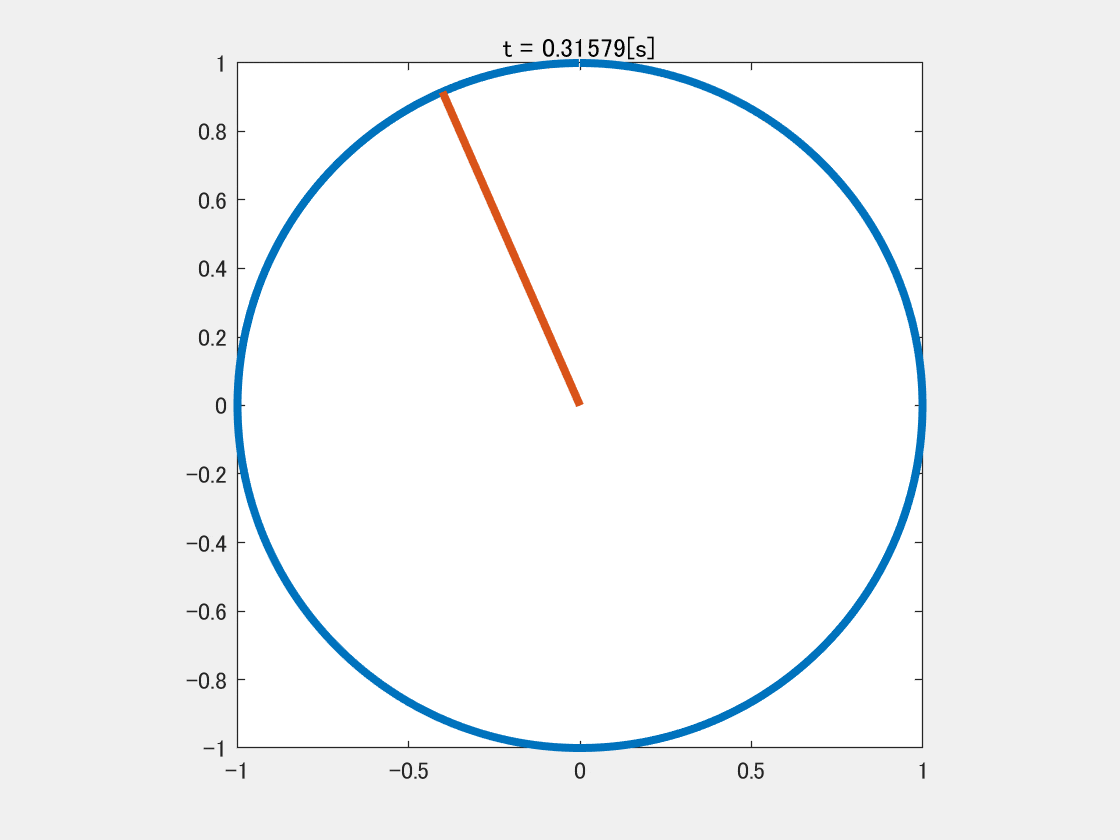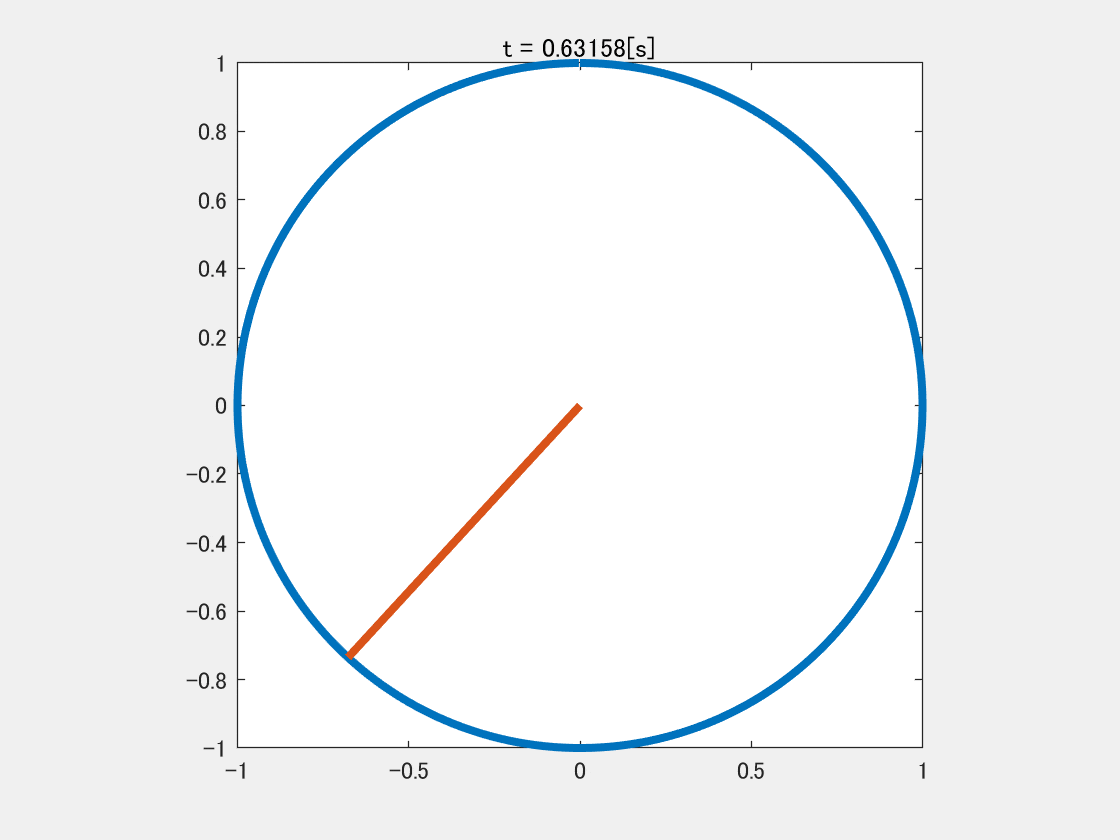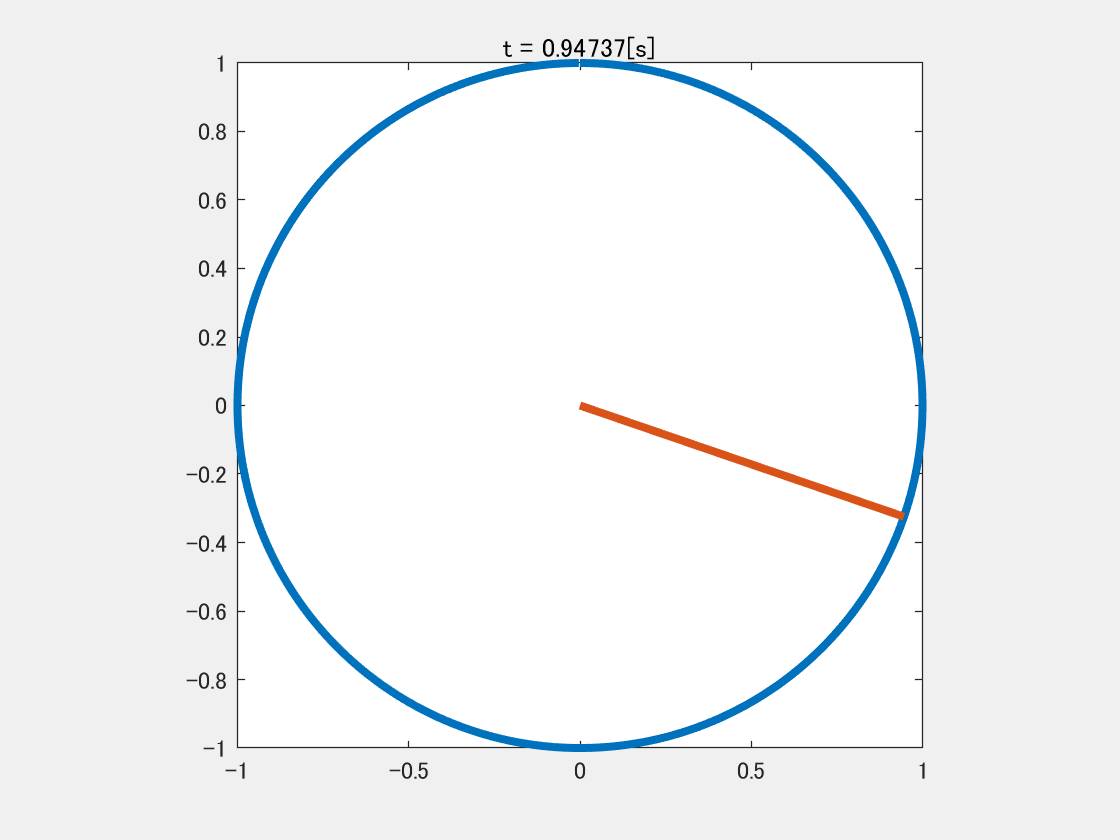
1秒間に1回転する信号
y = \sin ( x )\\(0 \le x < 2 \pi)
この式は学校で習ったと思われるが,$x=2 \pi$で$y$が$1$回転して元に戻る数式である.
これを以下のように書き換えてみる.
y = \sin ( 2 \pi t )\\(0 \le t < 1)
こう書くと今度は$t=1$になったら$1$回転することになる.
$t$の単位を秒とすると,上の式は$1$秒間で$1$回転し,これが$1[\rm{Hz}]$の信号である.
GIF画像の実装は↓
clc
clear all
close all
n0 = 0:0.01:2*pi;
F = 1;
t = linspace(0,1,20);
nImages = length(t);
fig = figure;
% アニメーションを1コマずつ作成する
for idx = 1:nImages
plot(sin(n0),cos(n0),'LineWidth',3);
hold on
x = [0 cos(2*pi*F*t(idx))];
y = [0 sin(2*pi*F*t(idx))];
plot(x,y,'LineWidth',3);
hold off
title(['t = ' num2str( t(idx),'%0.5f\n') '[s]' ]);
drawnow
axis([-1,1,-1,1]);
axis square
frame = getframe(fig);
im{idx} = frame2im(frame);
end
close;
filename = [num2str(F) 'Hz.gif'];
for idx = 1:nImages-1
[A,map] = rgb2ind(im{idx},256);
if idx == 1
imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.05);
else
imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.05);
end
end
次に,
y = \sin ( 2 \pi 2 t )
と書けば,$y$は$1$秒間に$2$周することになり,$2[\rm{Hz}]$の信号となる.(下図参照)
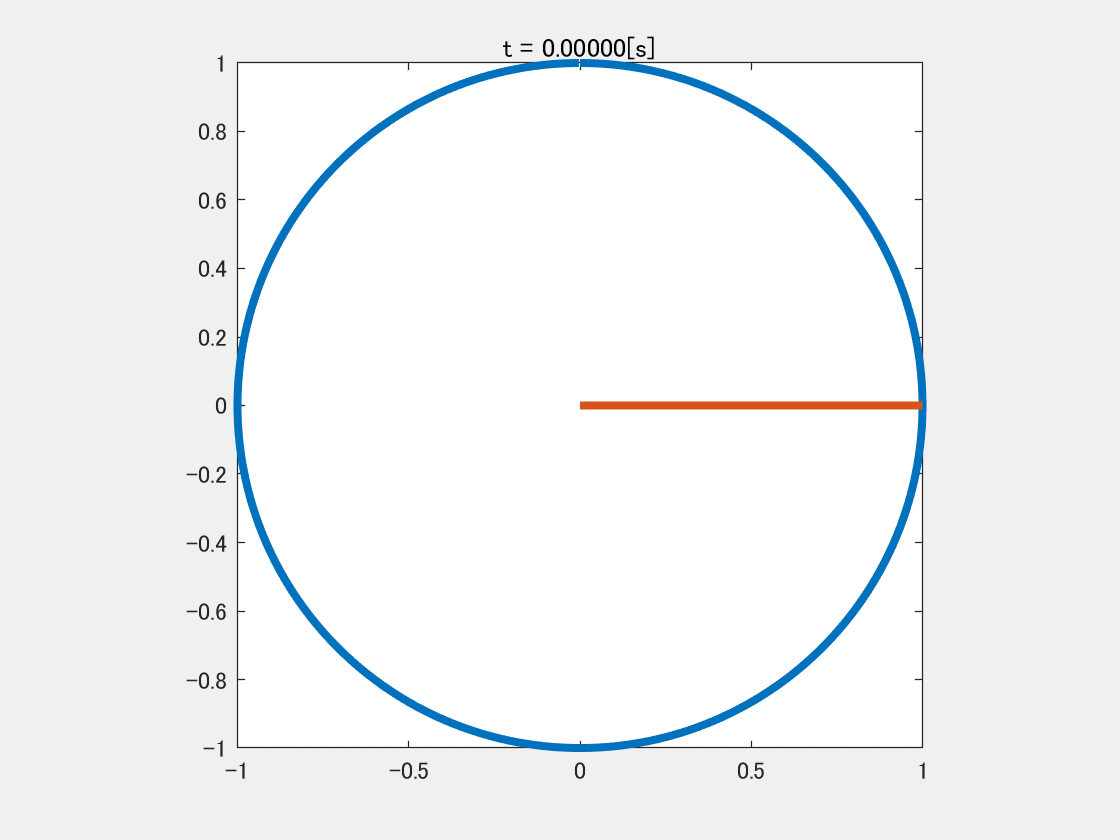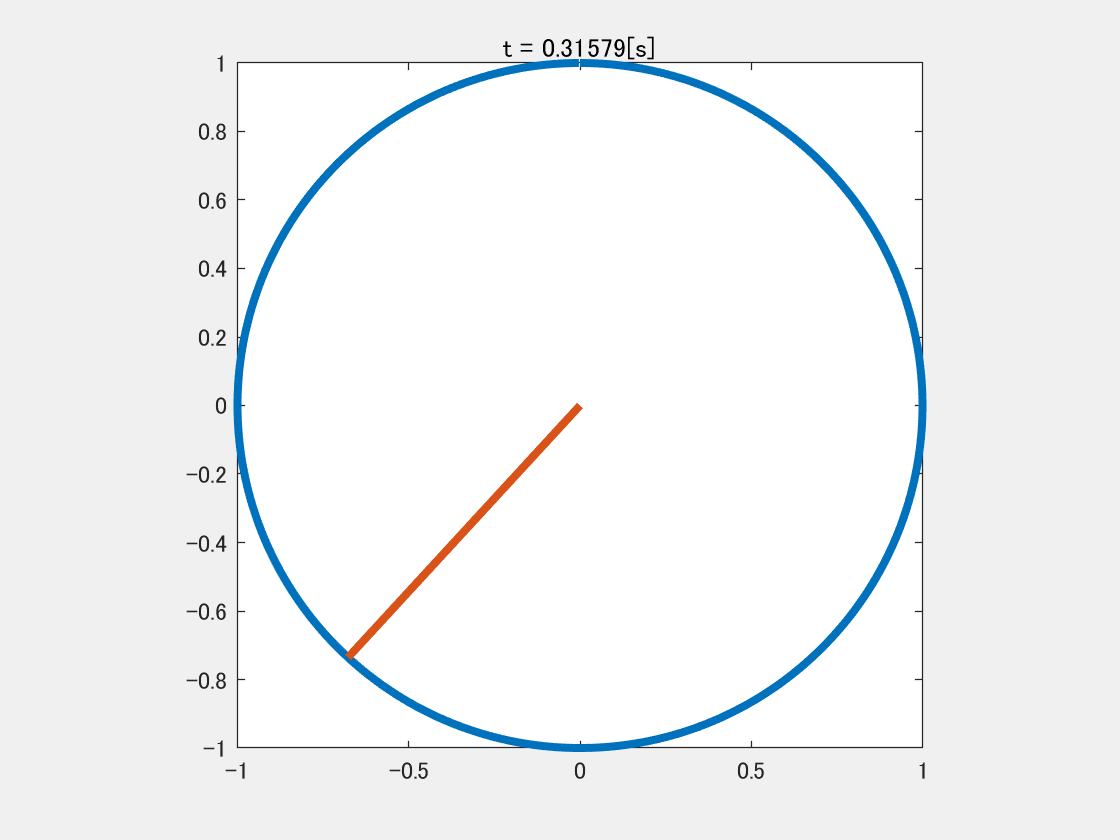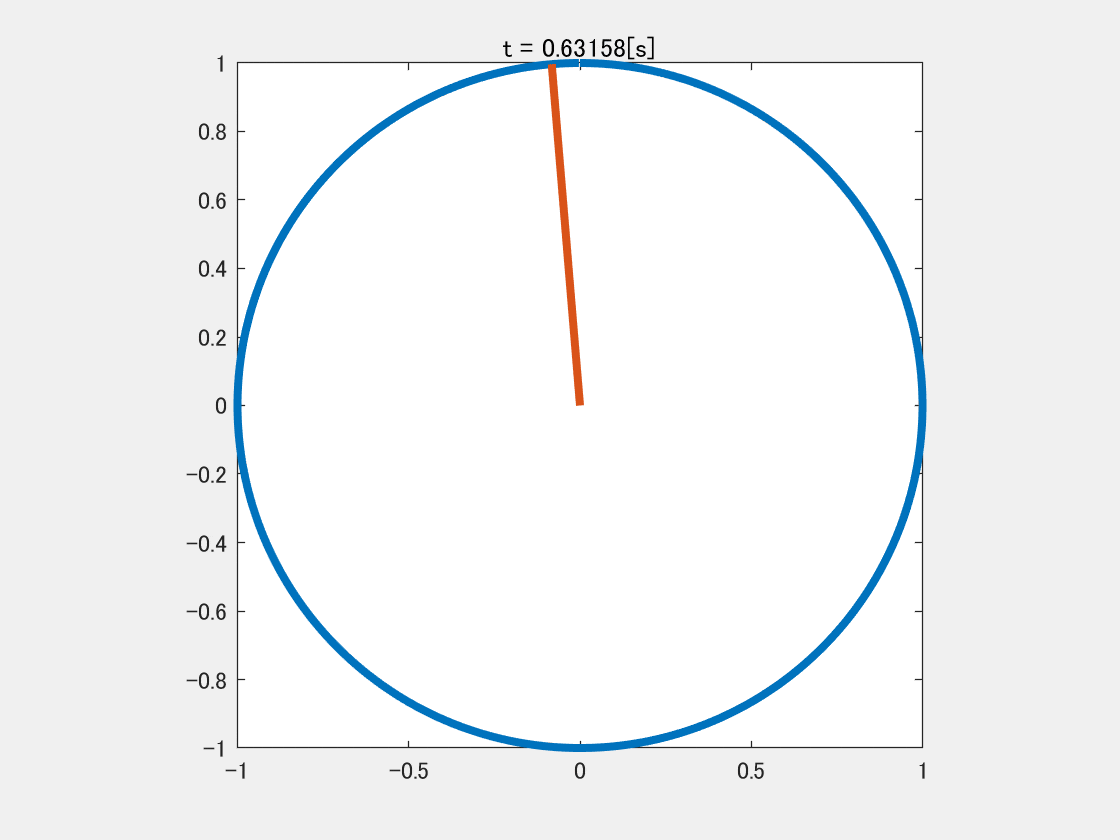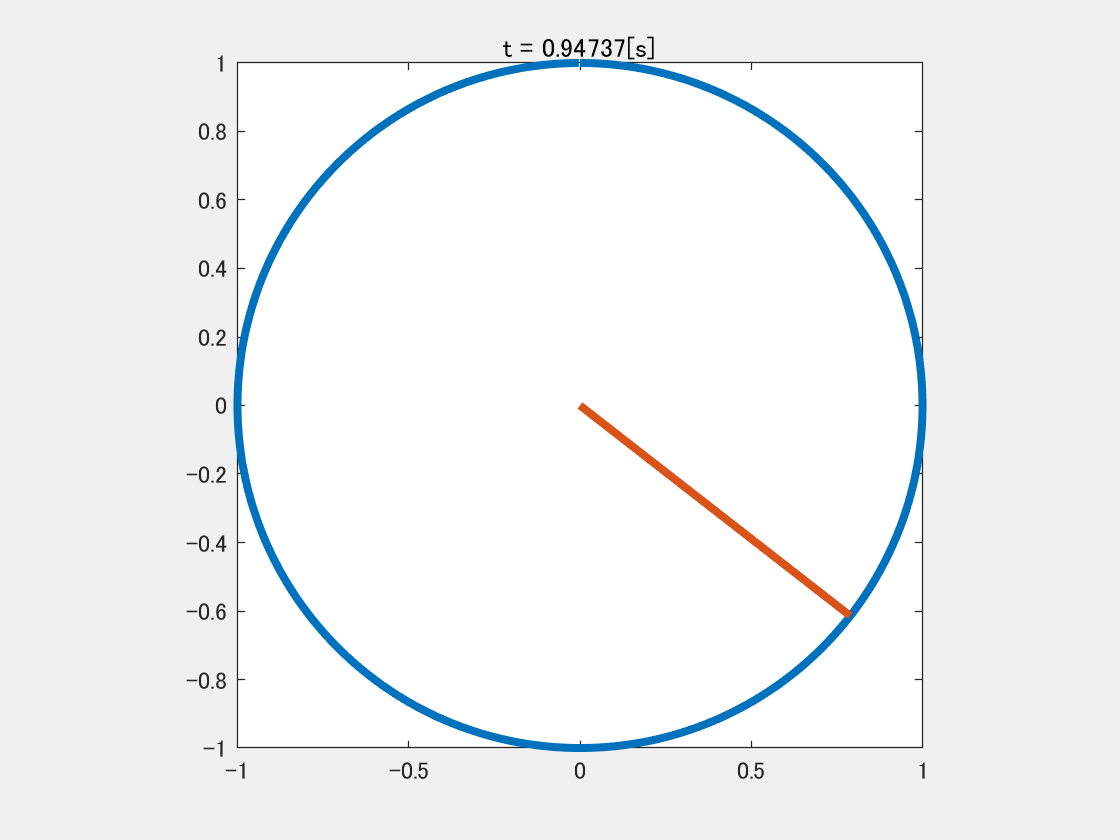
周波数一定の信号
以上の話をまとめると,周波数$f_c[\rm{Hz}]$(一定)で振動する信号は,
y = \sin ( 2 \pi f_c t )
と書ける.
周波数が時間変化する信号を考える
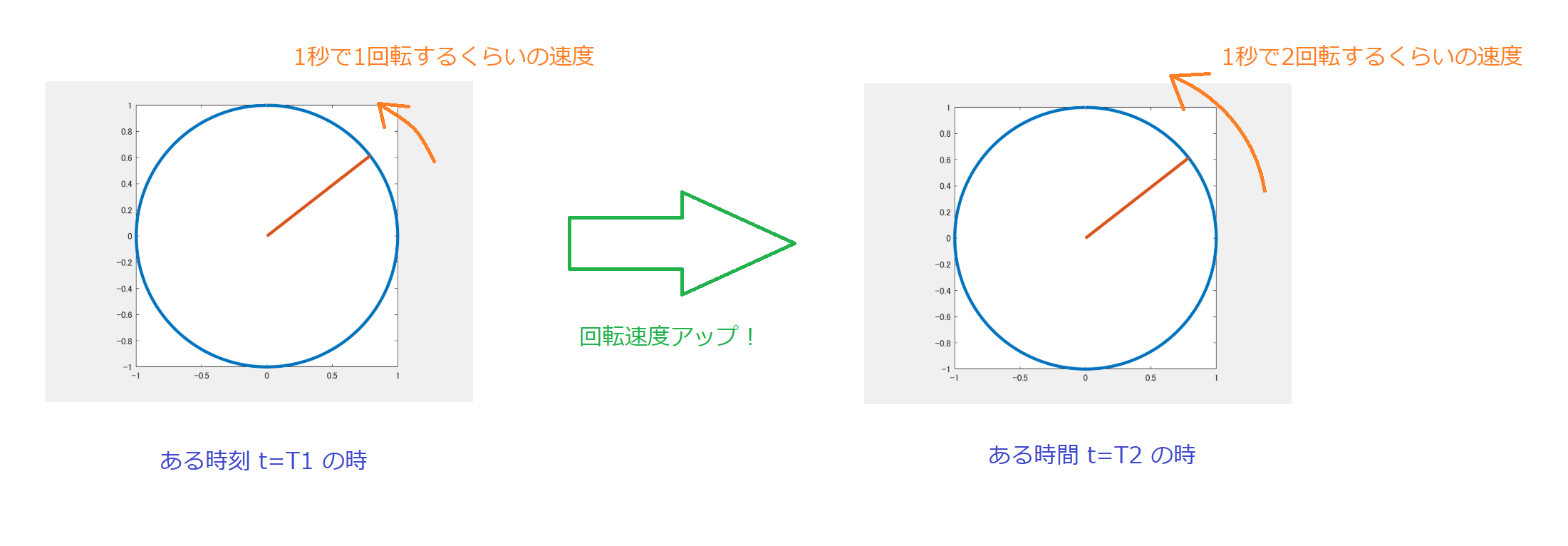
周波数が時間変化するとは,上の考え方で行くと,円周上を動く点の速度が速くなったり遅くなったりするということになる.
図にすると以下のような感じ.
これは周波数が$1[\rm{Hz}]$から$2[\rm{Hz}]$に時間変化した例である.
なお,周波数が変化することを変調と言い,周波数が線形に変調する信号を線形チャープ信号や,**LFM信号(Linear Frequency Modulation signal,線形周波数変調信号)**と言ったりする.
瞬時周波数
さて,周波数が時々刻々と変化する場合において,ある時刻における一瞬の周波数はどのようにして求めたらいいだろうか.
これは位相を時間で微分すると求められ,ある時刻の瞬間の周波数が瞬時周波数である.
周波数一定の信号の瞬時周波数
再度,周波数$f_c$(一定)の信号で考えてみる.
y = \sin ( 2 \pi f_c t )
位相$\phi (t)=2 \pi f_c t$を時間微分して,
f_i(t) = \frac{1}{2\pi}\frac{d}{dt} \phi (t) =\frac{1}{2\pi}\frac{d}{dt} ( 2 \pi f_c t ) = f_c \;\;({\rm constant})
周波数一定の信号の瞬時周波数$f_i=f_c$(一定)となり,期待通りである.
線形チャープ信号の瞬時周波数
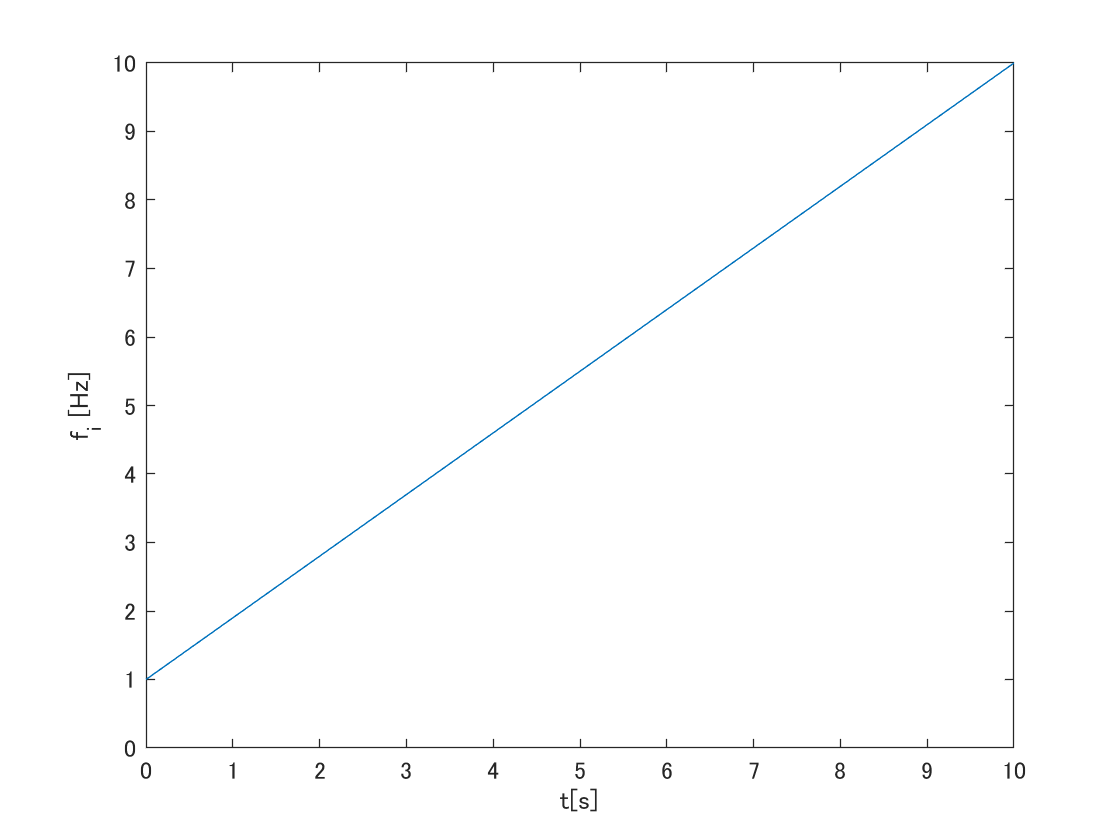
$t=0[\rm{s}]$で$1[\rm{Hz}]$の信号が,周波数が線形に増大していき,$t=10[\rm{s}]$で$10[\rm{Hz}]$になる線形チャープ信号を考える.
この数式は直線のY切片と傾きから,
f_i(t)= 0.9t+1
とすぐに求められる.
瞬時周波数から位相を求める
位相を時間で微分すると瞬時周波数が求められたので,逆に考えると,瞬時周波数を時間で積分すると位相が求められることになる.
\begin{align}
\phi (t)&= 2 \pi \int f_i dt\\
&=2 \pi \int (0.9t+1) dt\\
&=2 \pi \left( \frac{0.9}{2}t^2+t \right) + \phi _0 \\
\end{align}
積分定数の$\phi _0$は初期位相である.
これを$\sin()$の中に入れて,
\begin{align}
y =\sin \left(2 \pi \left( \frac{0.9}{2}t^2+t \right) + \phi _0 \right) \\
\end{align}
とすれば所望の線形チャープ信号が完成である.
matlabで確認
figure
Fs = 1000;
t=0:1/Fs:10;
y=sin(2*pi*(0.9/2*t.^2 + 1*t));%初期位相は0とした
plot(t,y);
ylim([-1 1])
ylabel('振幅')
xlabel('t[s]')
 という感じになり,sin波が時間経過でギューっと圧縮されており,確かに周波数がだんだんと高くなっているように見える.
という感じになり,sin波が時間経過でギューっと圧縮されており,確かに周波数がだんだんと高くなっているように見える.
スペクトログラム
基本的な時間周波数解析として,短時間フーリエ変換を使って信号のスペクトログラムを求めてみる.
Nw = 2048;
Nol = round(Nw/2);
NFFT = Nw;
spectrogram(y, Nw, Nol, NFFT, Fs, 'yaxis');
ylim([0, 10])
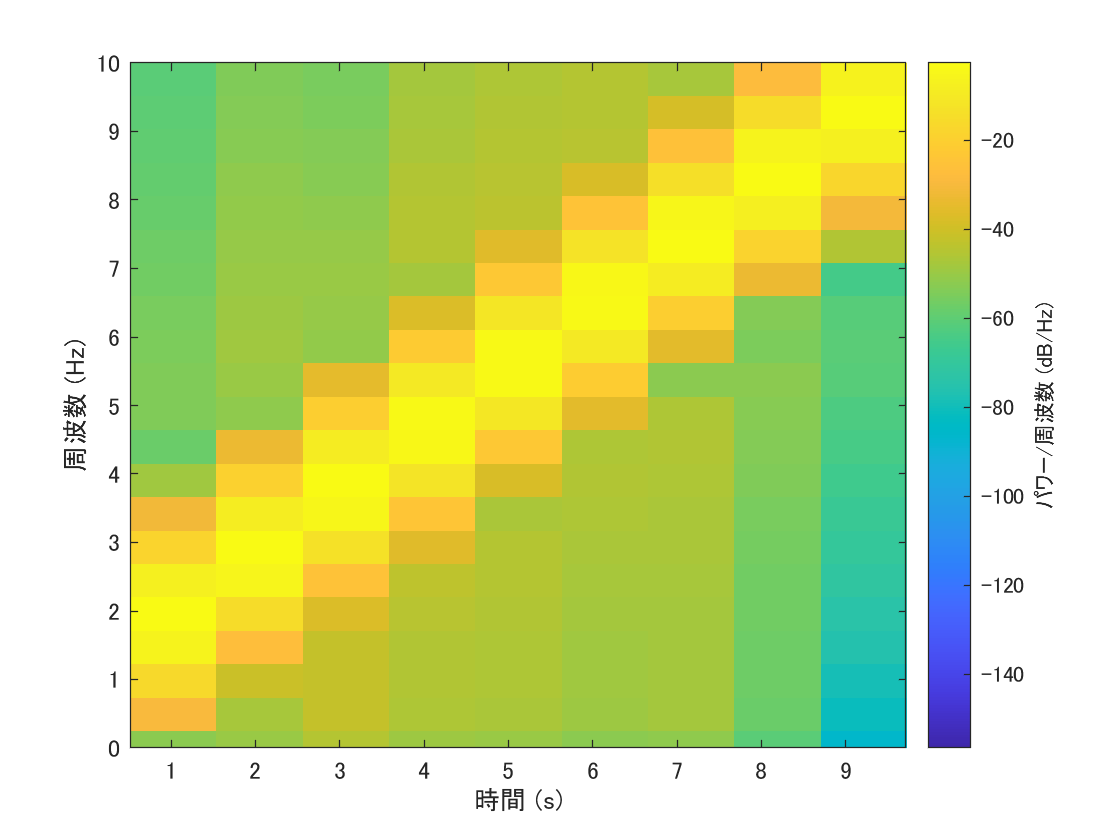
元の数式のグラフ(再掲)↓と比較して,同じような結果が得られた.
chirp関数
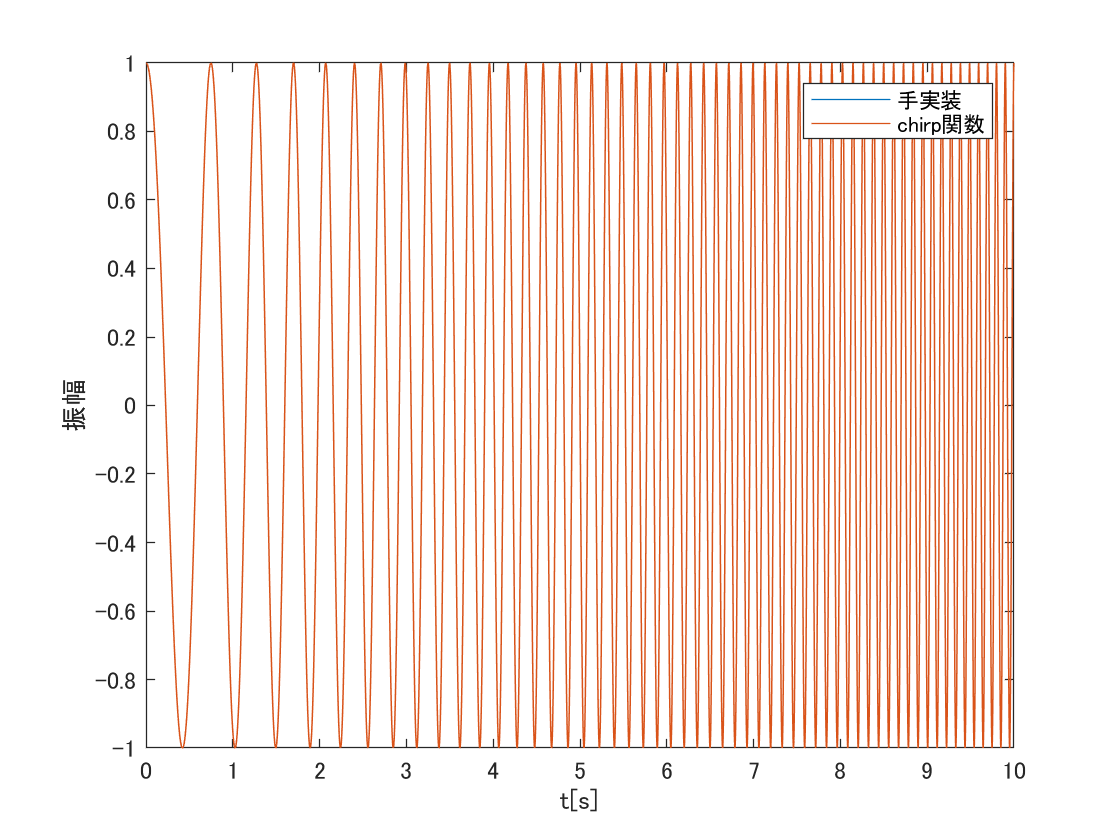
線形チャープ信号を手実装してみたが,matlabにはchirpというチャープ信号を生成する関数が標準で備わっている.
スイープ周波数の余弦信号 - MATLAB chirp - MathWorks 日本
chirpは$\cos$で実装されているので,上の式を書き換えて以下のようにする.
\begin{align}
y =\cos \left(2 \pi \left(\frac{0.9}{2}t^2+t\right) + \phi _0 \right) \\
\end{align}
figure
Fs = 1000;
t=0:1/Fs:10;
y=cos(2*pi*(0.9/2*t.^2 + 1*t));% 手実装
y2 = chirp(t,1,10,10);% matlab標準
plot(t,y);
hold on
plot(t,y2);
ylim([-1 1])
ylabel('振幅')
xlabel('t[s]')
legend('手実装', 'chirp関数')
% 確認
fprintf('norm=%f\n', norm(y-y2));% norm=0となれば両者は一致する
結果は下のようになり,ノルムは0となり,手実装したものとmatlab標準の結果が一致した.$\sin$で作ったものと見比べると位相が$90$度だけずれていることも分かる.
任意のチャープ信号を作ってみる
大体のチャープ信号はchirpを使えば作れちゃうので,今度はchirpでは作れない瞬時周波数を持つ信号を作成してみる.
瞬時周波数を以下のように定義する.
f_i(t) = 500 \sin (2 \pi t) + 500 t + 3000
瞬時周波数のグラフは以下となる.
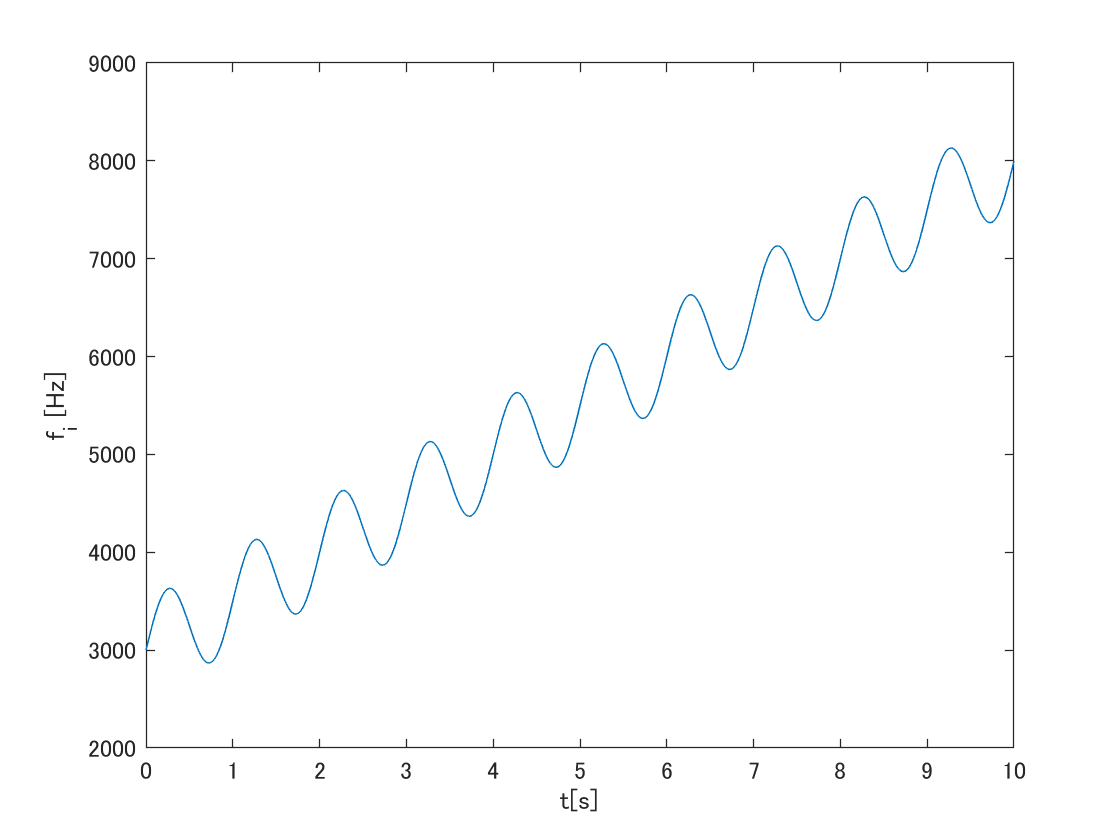
時間$t=0[{\rm s}]$で$f=3000[{\rm Hz}]$,そこからほわんほわんと周波数が高くなっていく信号である.
先ほどと同様に,$f_i$を積分して位相を求める.
\begin{align}
\phi (t)&= 2 \pi \int f_i dt\\
&=2 \pi \int (500 \sin (2 \pi t) + 500 t + 3000) dt\\
&=2 \pi \left( -\frac{500}{2 \pi} \cos (2 \pi t) + 250 t^2 + 3000t \right) + \phi _0\\
\end{align}
これを$\sin()$の中に入れて,
\begin{align}
y =\sin \left( 2 \pi \left( -\frac{500}{2 \pi} \cos (2 \pi t) + 250 t^2 + 3000t \right) + \phi _0 \right)\\
\end{align}
時間波形は下のようになって,これだけだときしめんになっててよく分からない.
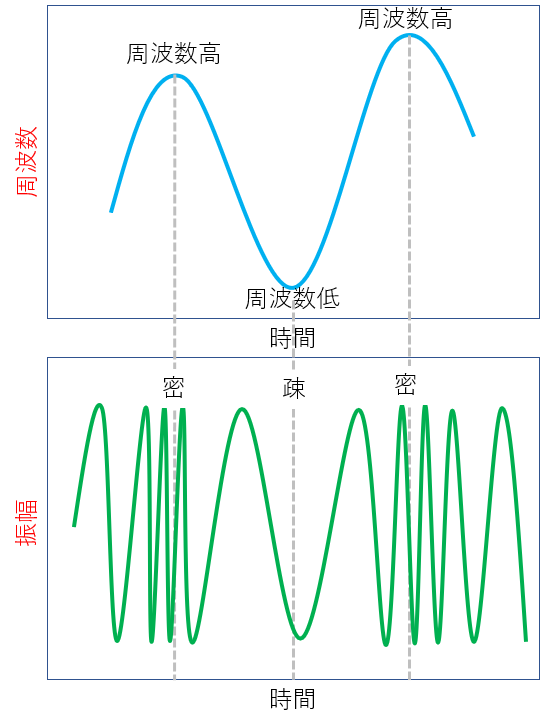
2021年11月20日追記:上のきしめんだと不親切だと思ったので,ざっくりとした図を描いてみた(下図).
時間周波数グラフと時間振幅グラフの対応がイメージ出来るようになっただろうか.
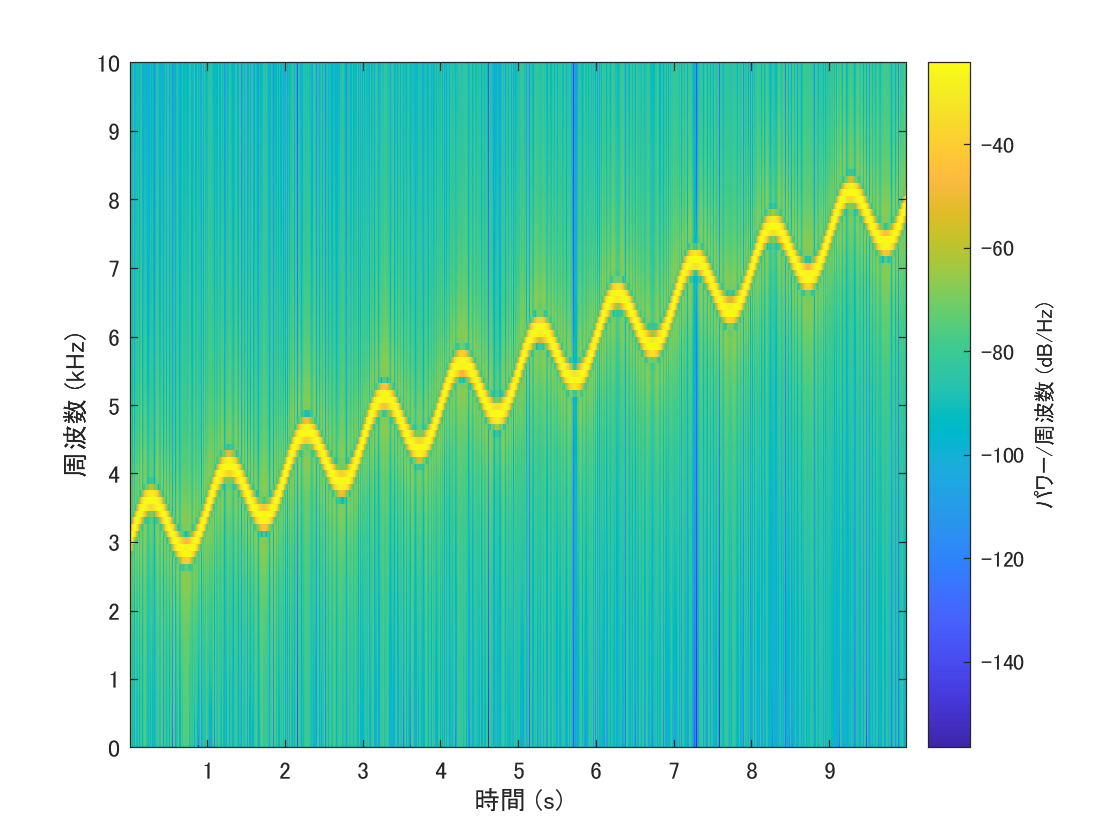
さて,スペクトログラムを求めてみると,確かに期待した結果となった.
補足(物理の速度と瞬時周波数を比較する)
例題の瞬時周波数は以下であった.
f_i(t)= 0.9t+1
これに$2 \pi$を掛けたものが瞬時位相である.
\phi _i(t)= 2 \pi (0.9t+1)
これを以下のように書き換える.
v(t)=a t + v_0
こう書くと,これは物理の授業で習った物体の速度である.
物体の移動距離は以下のように書ける.
x(t)=\int v(t)dt = \frac{1}{2} a t^2 + v_0 t
まとめると,以下の表になる.
| 速度の世界 | 周波数の世界 | |
|---|---|---|
| 距離 $x(t) = \frac{1}{2} a t^2 + v_0 t$ | 位相 $\phi(t) = 2 \pi \left( \frac{0.9}{2}t^2+t \right)$ | |
| $1$回微分 | 速度$v(t)=a t + v_0$ | 瞬時位相$f_i(t)= 2 \pi (0.9t+1)$ |
| $2$回微分 | 加速度$a$ | $\frac{d}{dt}f_i(t)= 2 \pi 0.9$ |
加速度に対応する,瞬時周波数(瞬時位相)を微分したものがどういう名前で定義されているかは分からなかった.
以上