はじめに
今回は時間周波数解析の一種であるウィグナーヴィレ分布について紹介し,スペクトログラムと比較しながらその利点と欠点について解説する.
詳しい計算を解説するとかなりのボリュームになるので,その辺は後日記事を書こうと思う.
今回は計算無しで行く.
ウィグナーヴィレ分布とは
計算無しで行くと言ったがとりあえず定義だけ書く.ウィグナーヴィレ分布$W(t,f)$は,入力信号$x(t)$の解析信号$z(t)=\mathcal{A}(x(t))$とすると以下のように定義される.
W(t,f)=\int ^ \infty _{-\infty} z\left(t+\frac{\tau}{2} \right)z^*\left(t-\frac{\tau}{2} \right) \mathrm{e}^{-j2 \pi f \tau} d\tau
解析信号とは入力信号を負の周波数を持たないように変換をした複素信号である.
なお,実数信号をそのまま用いるとウィグナー分布$\mathcal{W}(t,f)$になる.
\mathcal{W}(t,f)=\int ^ \infty _{-\infty} s\left(t+\frac{\tau}{2} \right)s\left(t-\frac{\tau}{2} \right) \mathrm{e}^{-j2 \pi f \tau} d\tau
ウィグナーヴィレ分布の特徴としてかなりシャープな結果を出してくれる.以下に例を挙げていこう.
例 1つのチャープ信号を分析してみる
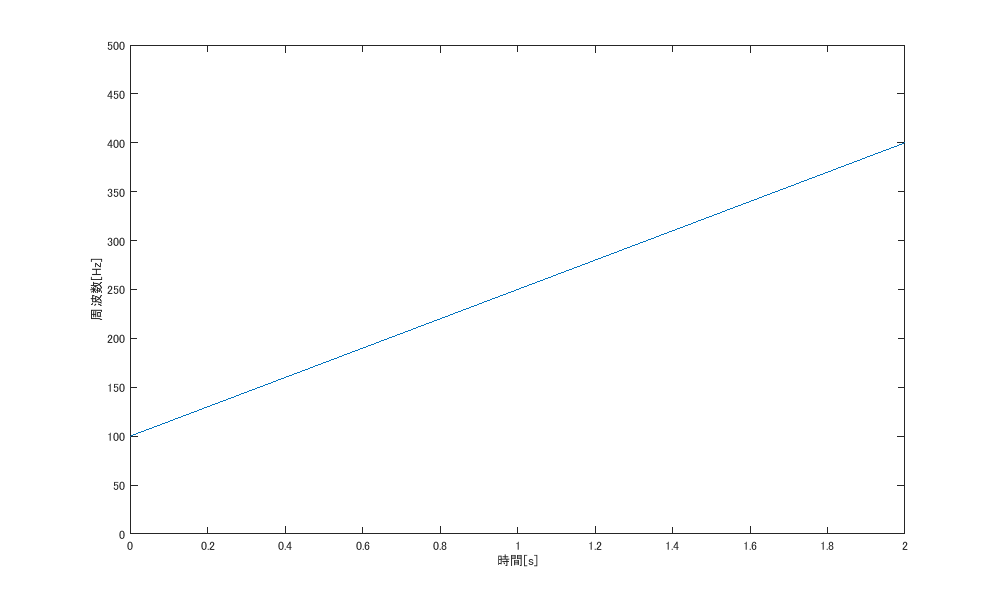
以下の瞬時周波数を持つチャープ信号を分析してみる.
f_i(t)=150t+100
チャープ信号の解説は↓
$t=0\rm{[s]}$で$f=100\rm{[Hz]}$であり,$t=1\rm{[s]}$ごとに$f=150\rm{[Hz]}$だけ周波数が高くなっていく信号である.
チャープ信号は,瞬時位相$\phi_i(t)=2 \pi f_i$を積分して$\sin$か$\cos$に突っ込めばよいので,
y(t)=\cos \left( 2 \pi \left( 150\frac{1}{2}t^2+100t \right) + \phi_0 \right)
時間波形は,
Fs = 1000;
T = 2;
N = Fs*T;
t = ((1:N)-1)/Fs;
fi = 150*t + 100;
figure('Position' , [100 100 1000 600])
plot(t,fi);
ylim([0,Fs/2]);
xlabel('時間[s]');
ylabel('周波数[Hz]');
phi = 150/2*t.^2 + 100*t;
y = cos(2*pi*(phi));
figure('Position' , [100 100 1000 600])
plot(t,y);
ylim([-1 1]);
xlabel('時間[s]');
ylabel('振幅');
スペクトログラムの結果
比較のため,一般的な時間周波数解析手法であるスペクトログラム(短時間フーリエ変換を絶対値の$2$乗したもの)で分析をする.
figure('Position', [100 100 1000 600])
Nw = 128;
Nol = round(Nw*0.95);
NFFT = Nw;
spectrogram(y, Nw, Nol, NFFT, Fs, 'yaxis');

ウィグナーヴィレ分布の結果
今回はSignal Processing Toolboxのwvdを使用する.
Wigner-Ville 分布と平滑化疑似 Wigner-Ville 分布 - MathWorks
figure('Position', [100 100 1000 600])
wvd(y, Fs);
caxis([0 1500])

スペクトログラムと比較して,めちゃくちゃシャープに結果が表示されていることが分かると思う.
スゴイ!
例 2つのチャープ信号
次は以下の瞬時周波数を持つ2つのチャープ信号を分析する.
f_1(t)=100t+200\\
f_2(t)=100t+50

解説及び`matlab`実装は↓
y(t) = \cos \left( 2 \pi \left( 100\frac{1}{2}t^2+100t \right) + \phi_0 \right)
+ \cos \left( 2 \pi \left( 100\frac{1}{2}t^2+50t \right) + \psi_0 \right)
Fs = 1000;
T = 2;
N = Fs*T;
t = ((1:N)-1)/Fs;
%fi = 150*t + 100;
fi1 = 100*t + 200;
fi2 = 100*t + 50;
figure('Position' , [100 100 1000 600])
plot(t,fi1);
hold on
plot(t,fi2);
ylim([0,Fs/2]);
xlabel('時間[s]');
ylabel('周波数[Hz]');
%phi = 150/2*t.^2 + 100*t;
phi = 100/2*t.^2 + 200*t;
phi2 = 100/2*t.^2 + 50*t;
y = cos(2*pi*(phi)) + cos(2*pi*(phi2));
figure('Position' , [100 100 1000 600])
plot(t,y);
ylim([-1 1]);
xlabel('時間[s]');
ylabel('振幅');
% スペクトログラム
figure('Position' , [100 100 1000 600])
Nw = 128;
Nol = round(Nw*0.95);
NFFT = Nw;
spectrogram(y, Nw, Nol, NFFT, Fs, 'yaxis');
% ウィグナーヴィレ分布
figure('Position' , [100 100 1000 600])
wvd(y, Fs);
caxis([0 1500]);% そのままだと線が見えづらかったので表示レベル範囲をちょと修正
スペクトログラムの結果
ウィグナーヴィレ分布の結果
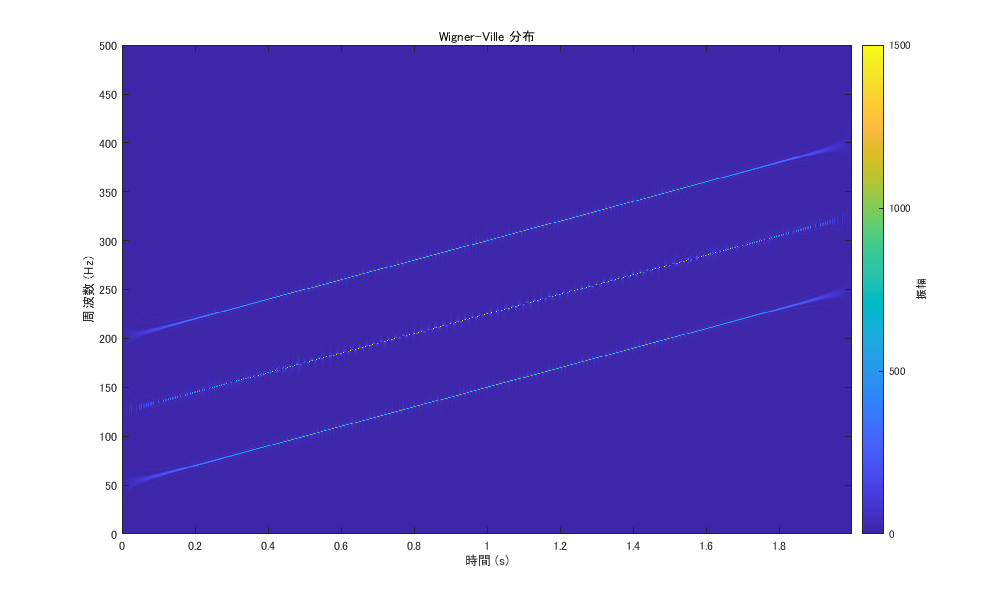
ん?

ウィグナーヴィレ分布では謎の線が出てしまっている.
例 2つのチャープ信号その2
気を取り直して,次はこちらの瞬時周波数を持つチャープ信号を分析しよう.
f_1(t)=100t+200\\
f_2(t)=-150t+400

解説及び`matlab`実装は↓
y(t) = \cos \left( 2 \pi \left( 100\frac{1}{2}t^2+100t \right) + \phi_0 \right)
+ \cos \left( 2 \pi \left( -150\frac{1}{2}t^2+400t \right) + \psi_0 \right)
phi = 100/2*t.^2 + 200*t;
phi2 = 100/2*t.^2 + 50*t;
y = cos(2*pi*(phi)) + cos(2*pi*(phi2));
% とすれば,あとは上と同じ.
%wvdの表示範囲は↓とした.
%caxis([0 1000])
スペクトログラムの結果

ウィグナーヴィレ分布の結果

ん~~~???

$2$線が交わる部分を拡大してみた.
縞模様のようなものが見えることが分かる.
ウィグナーヴィレ分布で発生する謎成分は何?
ウィグナーヴィレ分布で発生する謎のスペクトル成分(アーティファクト,偽像).
これをクロス項という.
計算は後日記事を書くことにするが,$z(t)=z_1(t)+z_2(t)$のウィグナーヴィレ分布は以下のようになる.
W_z=W_{z_1}+W_{z_2}+2\rm{Re}(W_{z_1 z_2})
ここで
W_{z_1 z_2}=\int ^ \infty _{-\infty} z_1\left(t+\frac{\tau}{2} \right)z_2^*\left(t-\frac{\tau}{2} \right) \mathrm{e}^{-j2 \pi f \tau} d\tau
この$W_{z_1 z_2}$がクロス項である.
 再掲.この図を見ると分かりやすいが,クロス項は$2$信号の**中間の位置**に発生する.
再掲.この図を見ると分かりやすいが,クロス項は$2$信号の**中間の位置**に発生する.
ウィグナーヴィレ分布はこのように,複数の信号があった場合に,クロス項が発生することが厄介な点である.
今回の例は単純なので分かりやすいが,実際の信号だとどれが本物の信号でどれがクロス項か判断がつかないことがある.
界隈ではこれを結果の解釈に専門性が問われると言ったりする.
ウィグナーヴィレ分布のその他の問題点
計算が遅い
メモリがかなり多めに必要だし,処理時間がかなりかかるようである.
位相の情報が失われる
逆変換が難しい.ウィグナーヴィレ分布を求めた後で時間周波数平面で雑音除去などの処理をして,それを再び音声データに戻すことが難しい.
クロス項の問題を解決する方法はあるの?
クロス項を抑制する方法は色々と研究されている.

再掲.これを見ると縞模様が出来ており,言い方を変えるとクロス項は時間方向や周波数方向に振動しているわけである.
よって,これにローパスフィルタをかけるとクロス項を抑制することが期待できる.
$(t-f)$平面ではなく,曖昧度関数$(\tau-\nu)$平面で処理をすることもある.
この辺を一般化した話がコーエンクラスである.
結果はボケボケだけど安定しているスペクトログラムと,結果はキレキレだけどクロス項が発生しちゃうウィグナーヴィレ分布.
キレキレの結果に平滑化フィルタをかけて結果をボカすのは元の木阿弥なのではと思うし実際平滑化フィルタとしてガウシアンをかけると結果がスペクトログラムになってしまうらしいのだが,このあたりは勉強中なので後日記事を書きたい。

