条件付き期待値(正規分布)を計算するGUIアプリを作る

問題

テストの点数$Z$が$N(50, 10^2)$に従うとき、平均点以上の人の点数の平均点を求めたい。

答え

正規化された$X$において、
$E[X|X\ge a]=\frac{\phi(a)}{1-\Phi(a)}$
ここで$\phi()$は正規分布の確率密度関数。
また$\Phi()$は正規分布の累積分布関数。

一般化する。正規分布$N(\mu, \sigma^2)$に従う$Y$において、
$E[Y|Y\ge b]=\mu + \sigma \frac{\phi(\frac{b-\mu}{\sigma})}{1-\Phi(\frac{b-\mu}{\sigma})}$となる。

よって、$E[Z|Z\ge50]=50 + 10\frac{\phi(0)}{1-\Phi(0)} = 50+10\frac{2}{\sqrt{\pi}} = 57.9788\dots$

計算したらそうなるというのはそれはそうなのですが、確率密度関数そのものが式中に登場するのが不思議です。

pythonでアプリを作ってみる

ChatGPTに作ってもらいました。本質的には

z = (x - mu) / sigma
p = 1 - norm.cdf(z)

conditional_mean = mu + sigma * norm.pdf(z) / p

が大事で、他はどうでもいいです。

ソースコード

import tkinter as tk
from tkinter import ttk
from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
import matplotlib_fontja

matplotlib_fontja.japanize()


def update_result(*args):
    try:
        mu = float(mu_var.get())
        sigma = float(sigma_var.get())
        x = float(x_var.get())
        if sigma <= 0:
            result_var.set("σ must be > 0")
            return

        z = (x - mu) / sigma
        p = 1 - norm.cdf(z)
        if p < 1e-8:
            result_var.set("P(X ≥ x) ≈ 0")
            ax.clear()
            canvas.draw()
            return

        conditional_mean = mu + sigma * norm.pdf(z) / p
        result_var.set(f"E[X | X ≥ x] ≈ {conditional_mean:.4f}")

        ax.clear()
        x_vals = np.linspace(mu - 4 * sigma, mu + 4 * sigma, 500)
        y_vals = norm.pdf(x_vals, loc=mu, scale=sigma)
        ax.plot(x_vals, y_vals, label="正規分布", color='blue')

        fill_x = np.linspace(x, mu + 4 * sigma, 300)
        fill_y = norm.pdf(fill_x, loc=mu, scale=sigma)
        ax.fill_between(fill_x, fill_y, color='orange', alpha=0.5, label="X >= x の領域")

        ax.axvline(x, color='red', linestyle='--', label=f"x = {x}")

        ax.set_title("条件付き期待値")
        ax.set_xlabel("x")
        ax.set_ylabel("確率密度")
        ax.legend()
        ax.grid(True)

        canvas.draw()

    except Exception as e:
        result_var.set("Invalid input", e)


root = tk.Tk()
root.title("条件付き期待値 E[X | X ≥ x]")

mu_var = tk.StringVar(value="50")
sigma_var = tk.StringVar(value="10")
x_var = tk.StringVar(value="60")
result_var = tk.StringVar()

frame = ttk.Frame(root, padding=[80, 20])
frame.grid()

ttk.Label(frame, text="μ (平均):").grid(column=0, row=0, sticky="e")
ttk.Entry(frame, textvariable=mu_var, width=10).grid(column=1, row=0)

ttk.Label(frame, text="σ (標準偏差):").grid(column=0, row=1, sticky="e")
ttk.Entry(frame, textvariable=sigma_var, width=10).grid(column=1, row=1)

ttk.Label(frame, text="x (しきい値):").grid(column=0, row=2, sticky="e")
ttk.Entry(frame, textvariable=x_var, width=10).grid(column=1, row=2)

ttk.Label(frame, textvariable=result_var, font=("Arial", 12, "bold"),
          padding=[0, 20, 0, 10]).grid(column=0, row=4, columnspan=2)

fig, ax = plt.subplots(figsize=(4, 2.5), dpi=50)
canvas = FigureCanvasTkAgg(fig, master=root)
canvas.get_tk_widget().grid(row=5, column=0, columnspan=2)

for var in (mu_var, sigma_var, x_var):
    var.trace_add("write", update_result)

update_result()
rootmainloop()

結果

オレンジより右側の領域での平均値を計算します。
例えば閾値70であれば、

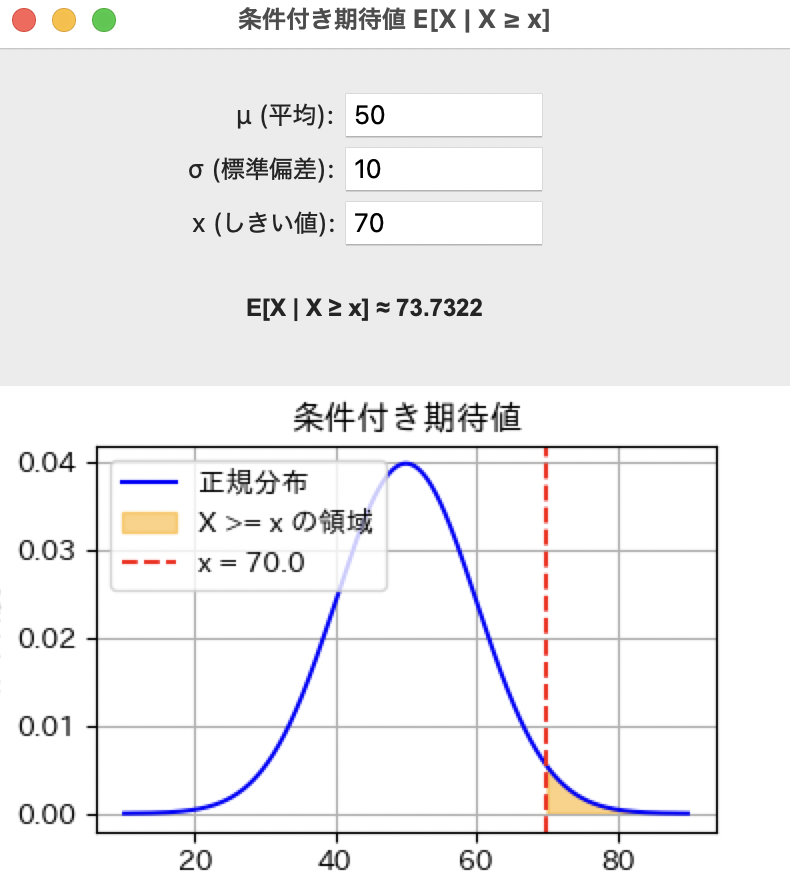
のようにして、平均点は73.7322であることが分かります。

ある閾値より上の点数の人たちの平均を取る→それを閾値に設定する、を繰り返すとどうなる？

気になったので。

条件付き期待値から平均を取り除いた部分$\sigma \frac{\phi(\frac{b-\mu}{\sigma})}{1-\Phi(\frac{b-\mu}{\sigma})}$は、$b$が大きくなることによって分子と分母はともに0に近づきます。一筋縄では行かなそうです。

面倒なので標準正規分布で考えましょう。仮にこの値が収束するのであれば、その収束値$c^*$は以下の方程式を解くことで得られます。

$$c=\frac{\phi(c)}{1-\Phi(c)}$$

右辺の関数は(標準正規分布における)逆ミルズ比と呼ばれるもののようです。この値を数値で解析しようとすると、一定以上の閾値では右辺の分母が非常に小さい値になるためにうまくいきません。

グラフの形状は逆ミルズ比が$x$に漸近する様子を示唆しています。

ここで、実は以下の方程式が成立するようです。

$$1-\Phi(z) < \frac{1}{z}\phi(z)$$

これを変形すると、

$$z < \frac{\phi(z)}{1-\Phi(z)}$$

となりますね。なので、$\sigma \frac{\phi(\frac{b-\mu}{\sigma})}{1-\Phi(\frac{b-\mu}{\sigma})}$は収束せず、章題の操作を繰り返すことによって閾値が収束することはない、というのが答えのようです。

所感

遊び心のままに些細な疑問を深掘ってみたわけですが、存外勉強になりました。

gitHub

参考