課題
判別分析手法について見ていきます。
問題設定
2元正規分布$N(0, I)$に従って生成された群Aと、同じく2元正規分布$N((2, 2)^\intercal, 0.5I)$に従って生成された群Bがあります。
これらは以下のソースコードで生成できます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
import matplotlib_fontja
matplotlib_fontja.japanize()
mean1 = [0, 0]
cov1 = [[1, 0], [0, 1]]
mean2 = [2, 2]
cov2 = [[0.5, 0], [0, 0.5]]
rv1 = multivariate_normal(mean=mean1, cov=cov1)
rv2 = multivariate_normal(mean=mean2, cov=cov2)
np.random.seed(0)
data1 = rv1.rvs(size=150)
data2 = rv2.rvs(size=20)
plt.scatter(data1[:, 0], data1[:, 1], alpha=0.6, label="Group 1")
plt.scatter(data2[:, 0], data2[:, 1], alpha=0.6, label="Group 2")
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
plt.title("2元正規分布のサンプル")
plt.grid(True)
plt.axis("equal")
plt.show()
群の情報が与えられていないときに、これらを判別する判別器を作成したいです。
LDA
フィッシャーの線形判別分析です。
あるベクトル$w$を用いてデータを射影しスカラー量に変形します。このときに、
$$\lambda(w)=\frac{群間分散}{群内分散}$$
が最大となる$\lambda$を見つける手法です。
ソースコード
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
mean1 = [0, 0]
cov1 = [[1, 0], [0, 1]]
mean2 = [2, 2]
cov2 = [[0.5, 0], [0, 0.5]]
rv1 = multivariate_normal(mean=mean1, cov=cov1)
rv2 = multivariate_normal(mean=mean2, cov=cov2)
np.random.seed(0)
data1 = rv1.rvs(size=150)
data2 = rv2.rvs(size=20)
X = np.vstack((data1, data2))
y = np.hstack((np.zeros(150), np.ones(20)))
lda = LinearDiscriminantAnalysis(
solver="svd", priors=[0.5, 0.5]
) # 事前分布は等しいと仮定
lda.fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 200), np.linspace(y_min, y_max, 200))
grid = np.c_[xx.ravel(), yy.ravel()]
Z = lda.predict(grid).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.2, levels=[-1, 0, 1], colors=["blue", "orange"])
plt.scatter(data1[:, 0], data1[:, 1], alpha=0.6, label="Group 1")
plt.scatter(data2[:, 0], data2[:, 1], alpha=0.6, label="Group 2")
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
plt.title("LDA with Equal Priors (Unequal Sample Sizes)")
plt.grid(True)
plt.axis("equal")
plt.show()
結果
事前分散が等しいと仮定しているので、数の多い群Aのデータのいくつかが群Bに取り込まれています。
LDAの計算式は $f(x) = \hat{w}^\intercal x-\frac{1}{2}(\bar{x}^{(1)}-\bar{x}^{(2)})^\intercal S^{-1} (\bar{x}^{(1)}+\bar{x}^{(2)})-log(\frac{\pi_2}{\pi_1})$と表され、最後の項が事前分布による補正項です。事前分布が等しいことを仮定しても同じ数だけ割り振られるわけではないのは、あくまで事前分布は補正項の形でしか現れないためです。
この場合の正誤表は以下のようになります。
Confusion Matrix:
[[136 14]
[ 0 20]]
Misclassification Rate: 0.0824
次に、事前分布を$(150/170, 20/170)$で指定してみます。
Confusion Matrix:
[[144 6]
[ 3 17]]
Misclassification Rate: 0.0529
誤判別率には多少の改善が見られますが、完璧な事前分布を与えたにしては、というような結果です。
SVM
ガウシアンカーネル・ソフトマージンを用いたSVMでも試してみます。
SVMでは入力を高次元空間に写像してそこで線形分離を行い、元の次元に戻すことで非線形な分類を行います。
ガウシアンカーネルはカーネル関数の一つで、放射状にデータを分類する能力を持ちます。
ソフトマージンはハードマージンの対立概念で、多少の誤分類を許容してより汎化性能の高い分類器を目指すための仕組みです。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
meanA = [0, 0]
covA = [[1, 0], [0, 1]]
meanB = [2, 2]
covB = [[0.5, 0], [0, 0.5]]
rvA = multivariate_normal(mean=meanA, cov=covA)
rvB = multivariate_normal(mean=meanB, cov=covB)
np.random.seed(0)
dataA = rvA.rvs(size=150)
dataB = rvB.rvs(size=20)
X = np.vstack((dataA, dataB))
y_true = np.hstack((np.zeros(150), np.ones(20)))
svm = SVC(kernel="rbf", C=1.0, gamma="scale")
svm.fit(X, y_true)
y_pred = svm.predict(X)
cm = confusion_matrix(y_true, y_pred)
print(cm)
misclassification_rate = 1 - np.trace(cm) / np.sum(cm)
print(f"{misclassification_rate:.4f}")
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300), np.linspace(y_min, y_max, 300))
grid = np.c_[xx.ravel(), yy.ravel()]
Z = svm.predict(grid).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.2, levels=[-1, 0, 1], colors=["blue", "orange"])
plt.scatter(dataA[:, 0], dataA[:, 1], alpha=0.6, label="Group A")
plt.scatter(dataB[:, 0], dataB[:, 1], alpha=0.6, label="Group B")
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
plt.title("SVM with Gaussian Kernel")
plt.grid(True)
plt.axis("equal")
plt.show()
[[144 6]
[ 4 16]]
0.0588
色々なカーネル関数を試してみる
多項式
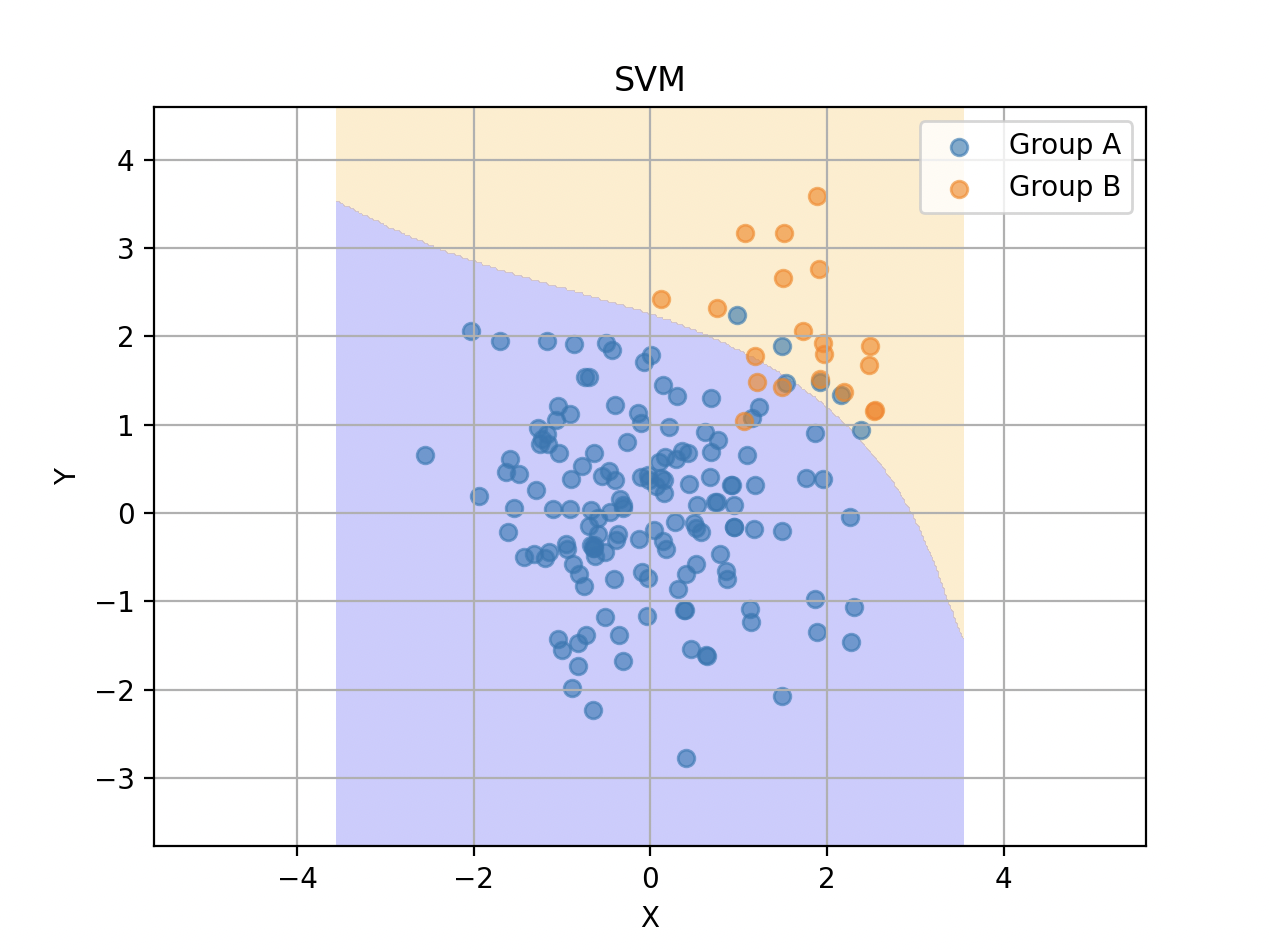
線形
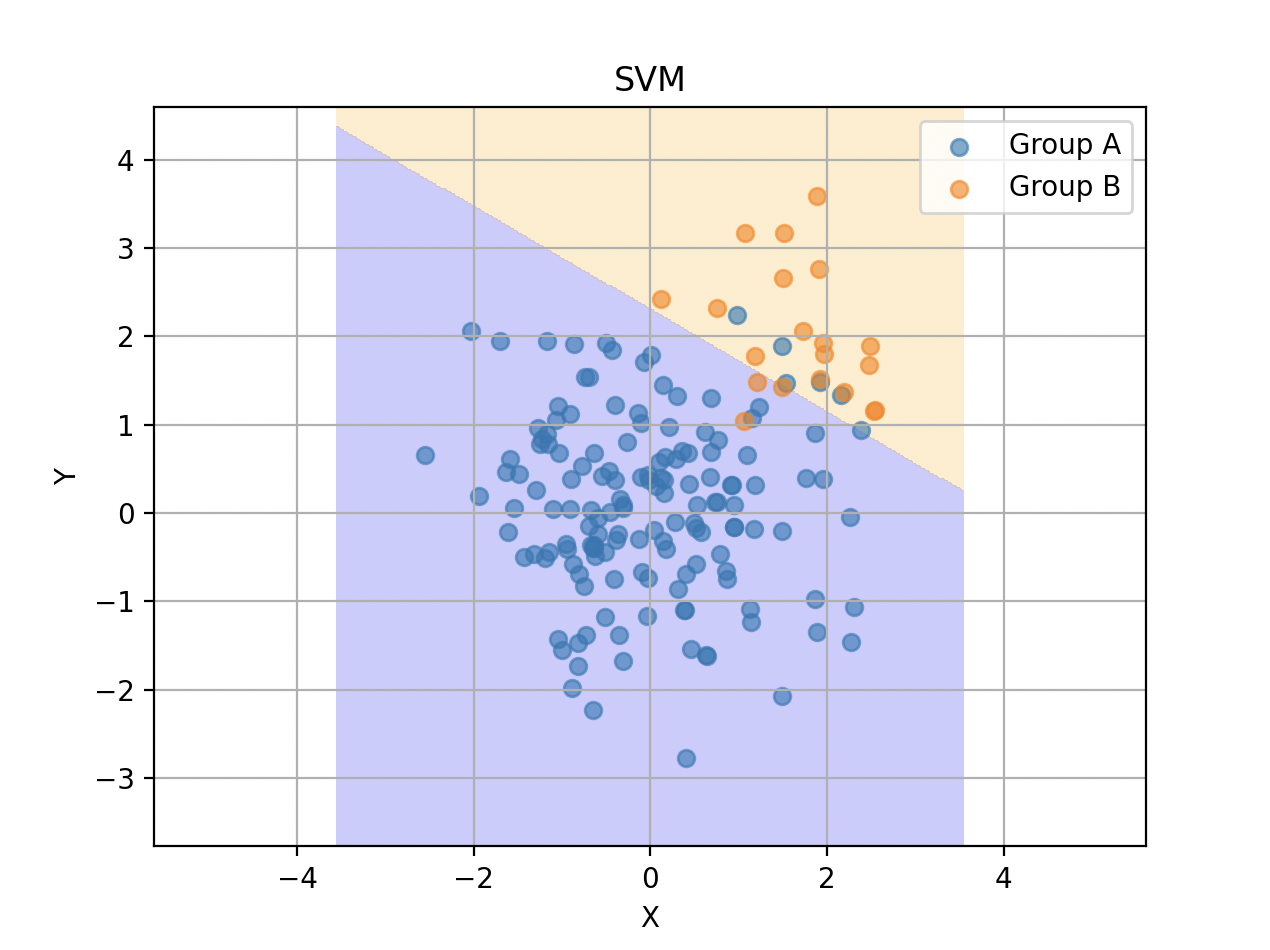
シグモイド
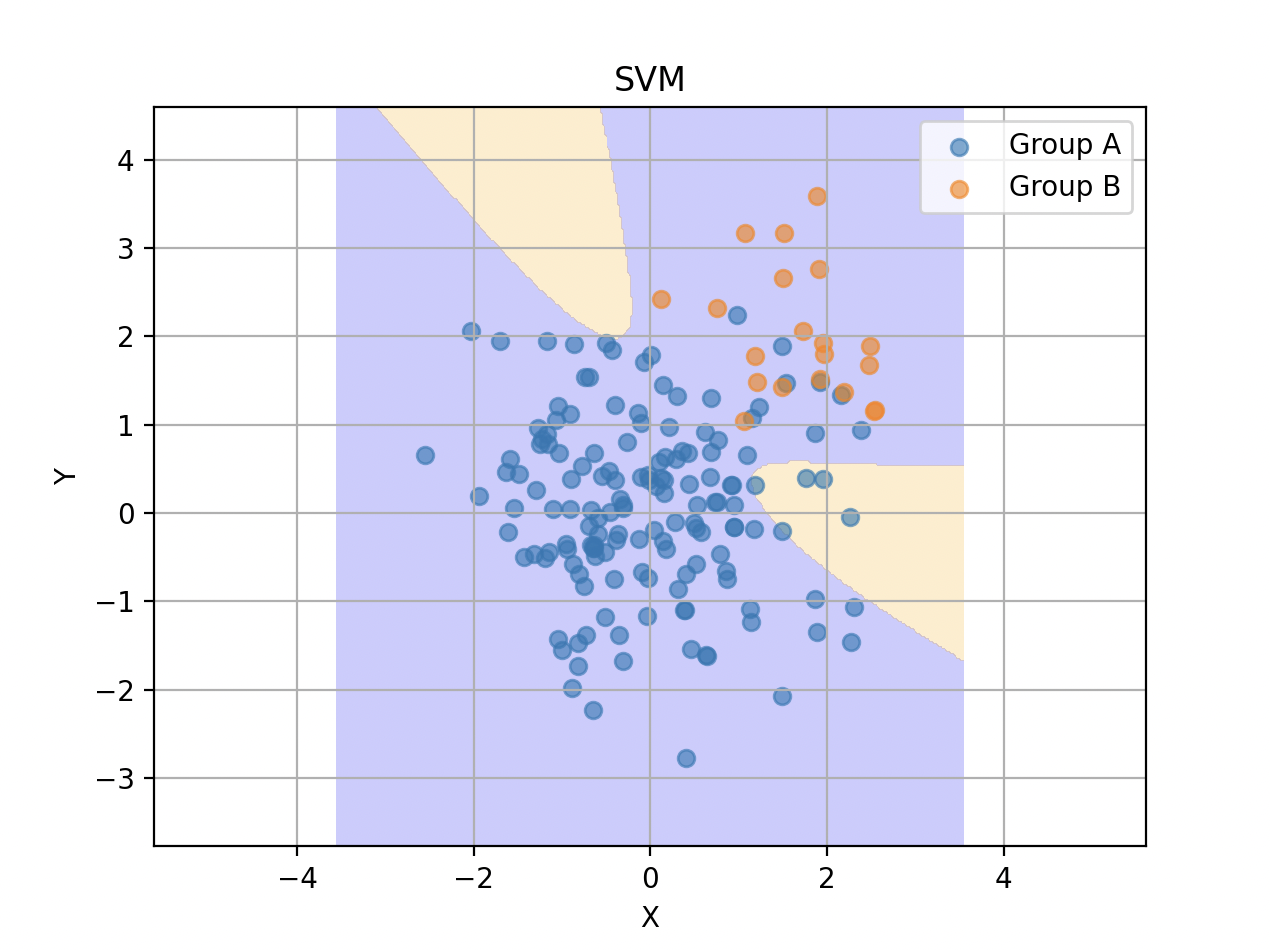
大失敗しています。
シグモイドカーネルは放射状の分類に弱い性質があるらしく、かつそもそもシグモイドカーネル自体の実用性を疑う向きがあるようです。
カーネル関数のパラメータ
ガウシアンカーネルの指定では、
svm = SVC(kernel="rbf", C=1.0, gamma="scale")
というように、ハイパーパラメータ$C$や$\gamma$を指定することができます。
C
誤分類のペナルティを調整します。
Cが大きいと誤分類に厳しくなり、マージンを犠牲にしてでも分類精度を重視するようになります。過学習を引き起こす可能性が高まります。
以下はcに100を指定したものです。誤判別率は$0.0412$で小さくなっていますが、過学習の気配がします。
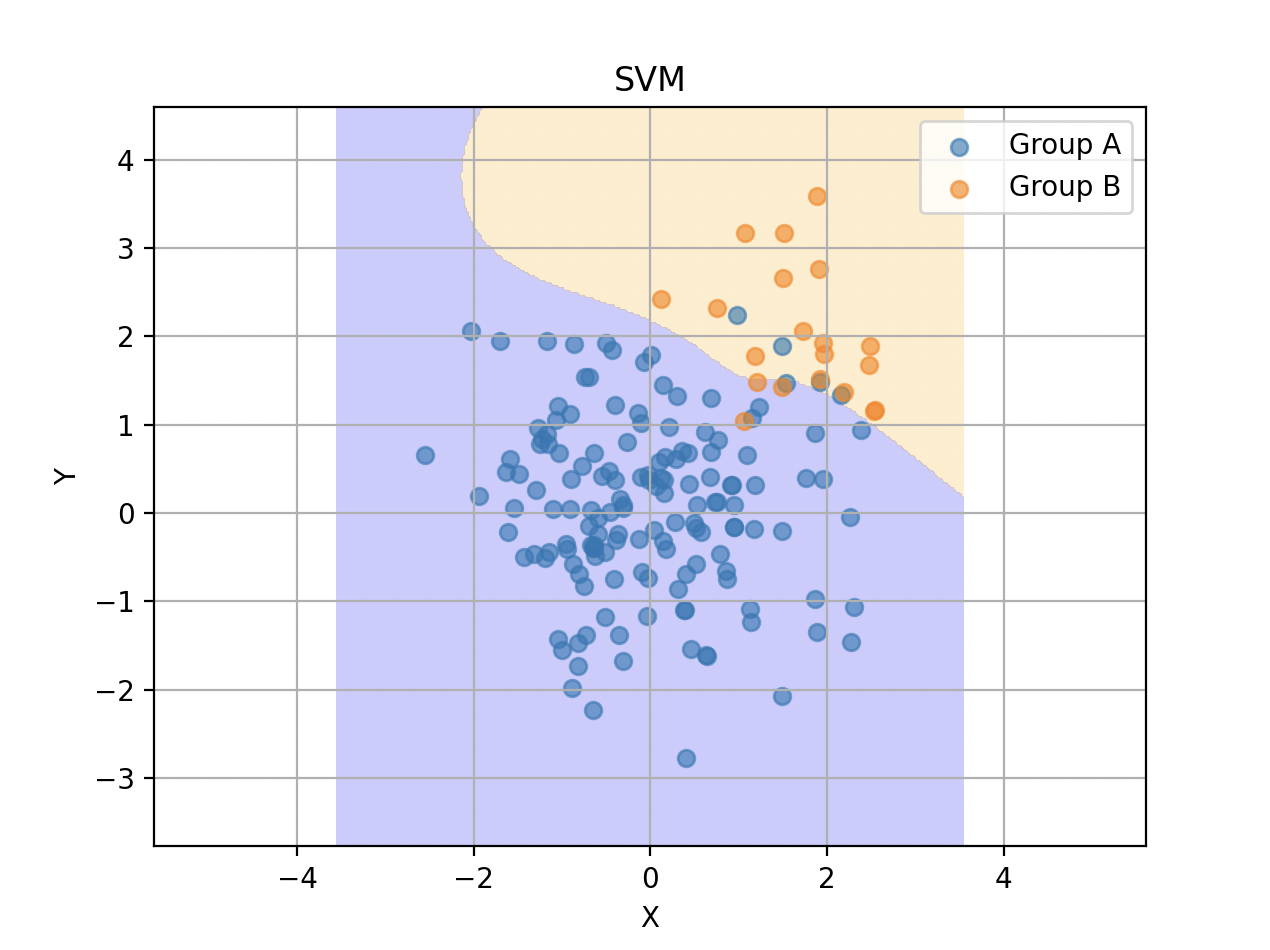
cに10000を指定すると、以下のようになりました。実際には小さい青色の領域にオレンジ色のサンプルが多くプロットされうるので、これはもう立派な過学習ですね。
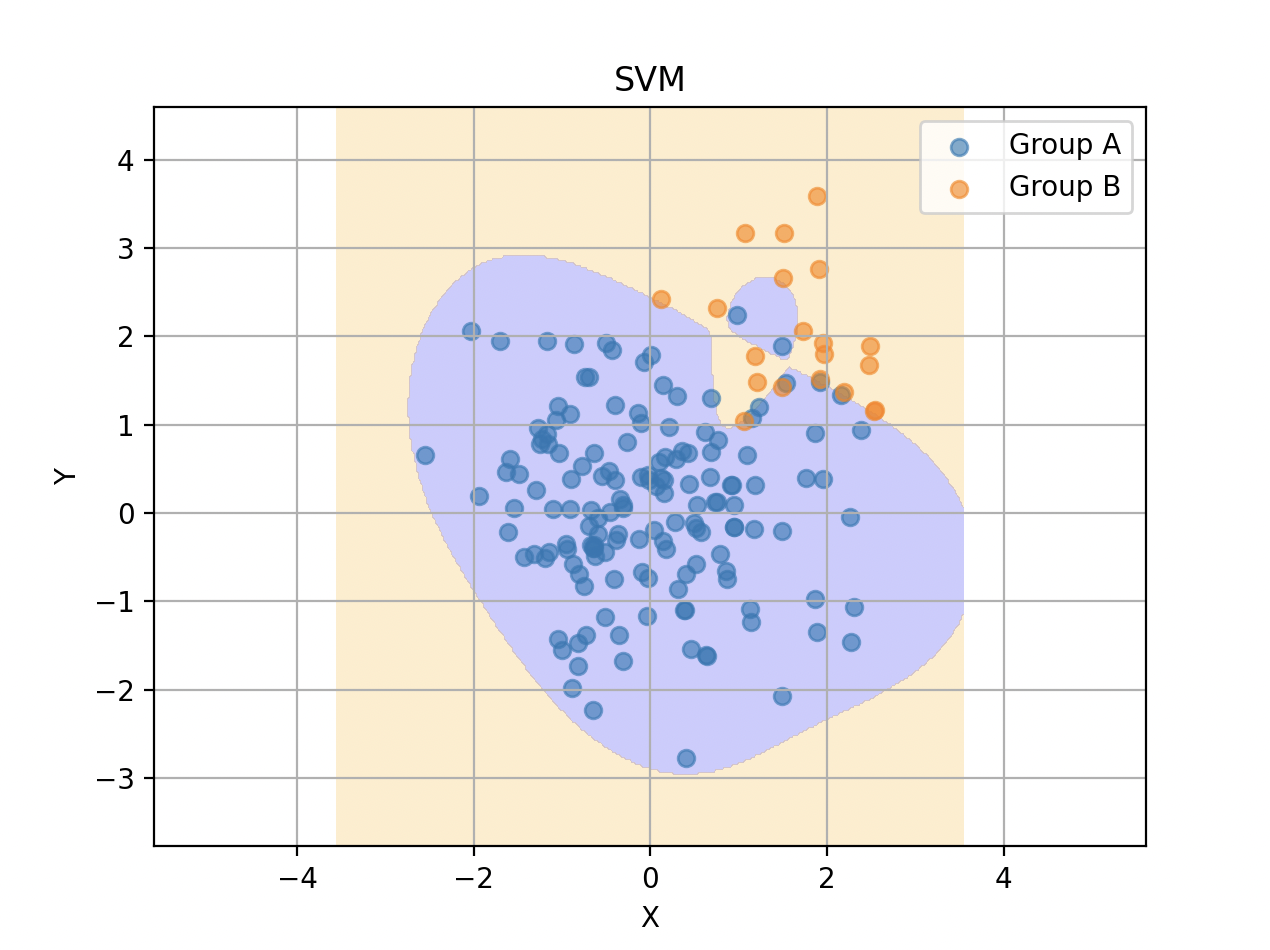
gamma
$\gamma$が大きいと各データの持つ影響範囲が小さくなり、決定境界が複雑になります。過学習を引き起こす可能性が高まります。
"scale"を指定するとデータから自動で計算して設定してくれるようです。数値で指定することもできて、例えば0.1を指定すると
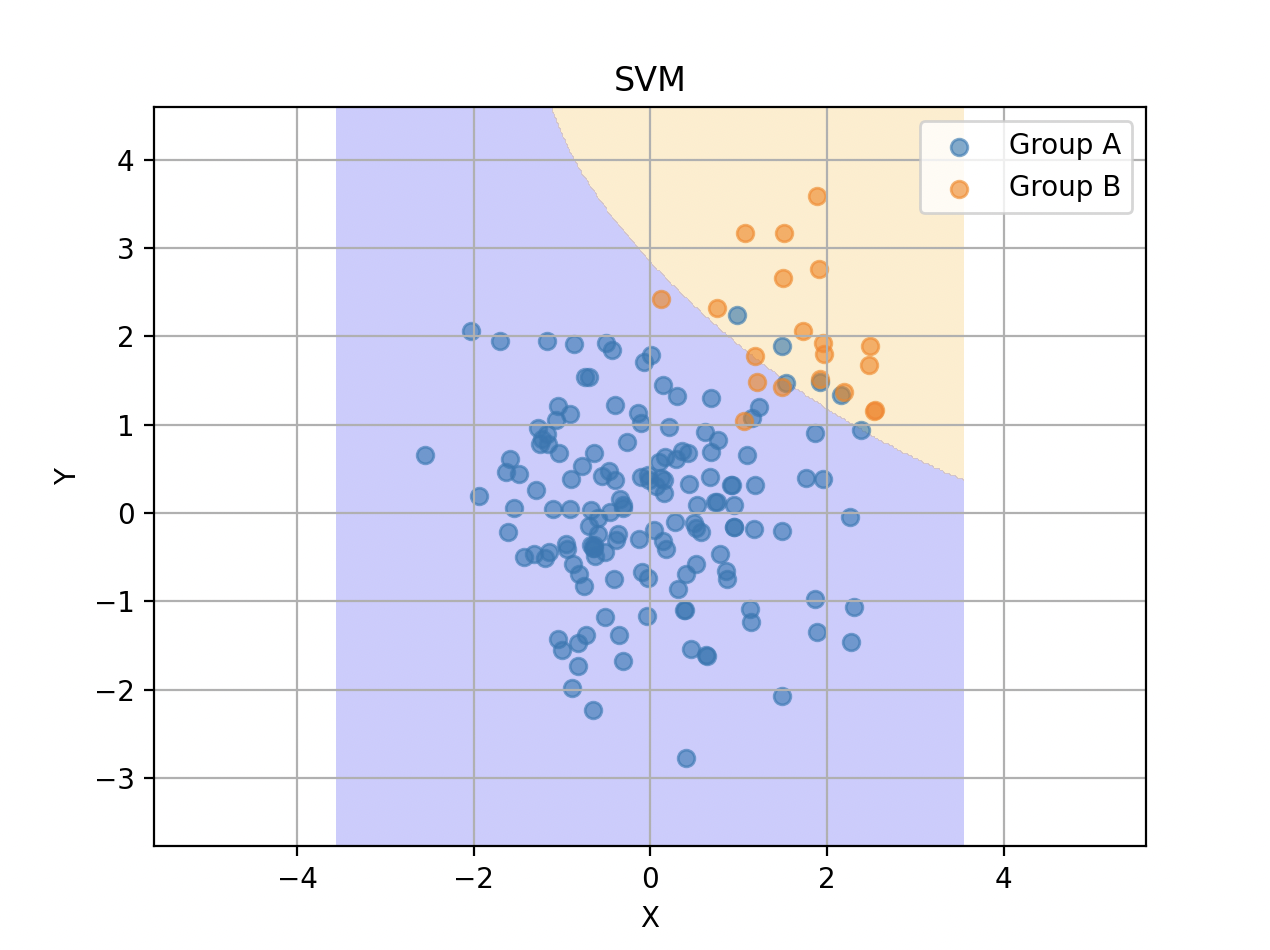
と、よりシンプルな境界になります。逆に10を指定すれば、

と、非常に複雑な境界となります。
所感
カーネルトリックを理解することは難しいかもしれませんが、理解することよりもブラックボックス的に把握すれば十分なのかもしれません。
GitHub



