PBD?
PBDはPosition Based Dynamicsの略です。分野としてはCGです。2006年と割と古いです。
Position Based Dynamics
ポエム
みなさんはゲームを作ったことがあるでしょうか。僕は、ゲームっぽいのは作ったことがあります。シューティングゲーム?RPG?アクション?作っていると分かりますが、学校で習った数学や物理の知識を割と使いますよね。最近では物理エンジンを搭載したゲーム開発環境も出てきて、そんなの気にしなくて良くなりましたが、きっちりと作るとなるとやはり考えなくてはなりません。例えば、ゲームにリアリティを出すと、物体に力を加えて、そこから速度を出して、位置を出して、、、みたな処理になると思います。
この論文では、先に位置を決定してそこから速度を計算していきます。
何が良いの?
家庭用ゲーム機なんかは私たちが普段使うPCよりもだいぶスペックが落ちます。また、FPSなんかのオンラインゲームでは処理の即時性が求められます。こういった限られた計算リソース、計算時間の中できっちりしたシミュレーションなんてしていられませんね。でも、やっぱりそれっぽい動きはしてほしいです。まあ、そういうわけでPBDを使うと再現性は落ちるけど計算時間は安定して軽くなるみたいな感じです。
長かったですけど、本題です。
本題
概要
これまでのCGにおける物理計算は、物体に加えられた力から加速度>速度>位置といった順で求められてきました。力から加速度は運動方程式より求められますね。加速度から速度や位置は物理で公式を習ったと思います。
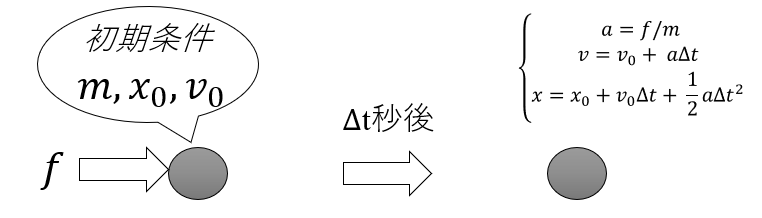
何もない空間ではこれで十分です。しかし、Δt秒後の移動先に物体があった場合はどうなるでしょうか。もちろん衝突判定を行って物体を正しい位置に戻さなければなりません。これにより、速度やポテンシャルの修正も行われるはずです。また、変形可能な物体では衝突による変形も考慮しなければなりません。
PBDでは、速度から位置を求めるのではなく位置から速度を求めていきます。こうすることで位置と速度、ポテンシャルとの整合性が取れます。以下の図が大まかな処理順です。中川氏のPosition Based Dynamics Combo 物理シミュレーション関連の最新論文実装より参考にさせていただきました。

最初はとりあえず速度をもとに位置を求めます。Explicit Euler法は「前回の位置に、Δtと速度の積を足せば次の位置が出るよね」っていうだけの簡単な方法です。位置が求まったら拘束条件というものを考えます。この考え方がPBDでは非常に大切です。例えば、上の図では非侵入拘束という風に考えられ
$$C(\vec{p_1}, \vec{p_2})=|\vec{p_1}-\vec{p_2}|-2r\quad(\vec{p_i}:円の中心座標,\quad r:半径)$$
と定義できます。この拘束条件を満たす、すなわちC=0となるように移動量Δpを求め、位置を修正していきます。上の図では、Δpは
$$\Delta\vec{p}=\pm(|\vec{p_1}-\vec{p_2}|-2r)\frac{\vec{p_1}-\vec{p_2}}{|\vec{p_1}-\vec{p_2}|}$$
と定義でき、実際に位置を修正・確定させます。最後に、実際の位置と前回の位置との差とΔtから速度を導き出します。
大まかにはこんな感じです。拘束条件についてもう少し詳しく見てみましょう。
拘束条件
PBDでは、この拘束条件の理解が一番肝要なものだと思っています。またまた、中川氏のスライドを参考にさせてもらいます。以下の図を見てください。
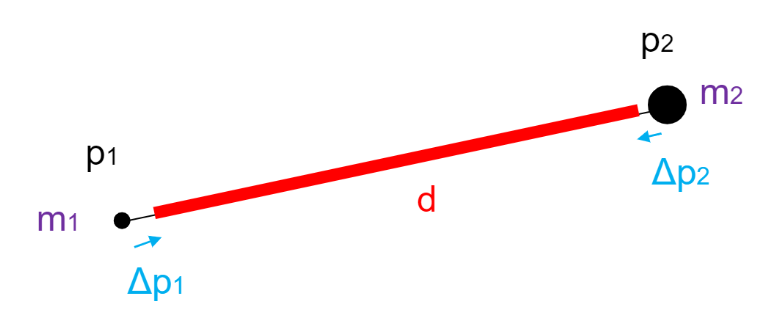
これは二つの質点p1,p2がある一定の距離dで存在するという拘束条件です。まあ、要するに以下の式で表されます。
$$C_{stretch}(\vec{p_1},\vec{p_2})=|\vec{p_1}-\vec{p_2}|-d$$
この式の値が0になれば拘束条件を満たすことになるわけです。では、この拘束条件を満たすような位置への移動量Δpはどういった式になるでしょうか。
$$\Delta\vec{p}=\pm(|\vec{p_1}-\vec{p_2}|-d)\frac{\vec{p_1}-\vec{p_2}}{|\vec{p_1}-\vec{p_2}|}$$
さきほどの概要で見たものと同じような式になりますね。しかし、質量が加味されていません。ということでもう少し工夫します。
$$\Delta\vec{p_1}=-\frac{w_1}{w_1+w_2}(|\vec{p_1}-\vec{p_2}|-d)\frac{\vec{p_1}-\vec{p_2}}{|\vec{p_1}-\vec{p_2}|}\qquad \Delta\vec{p_2}=+\frac{w_2}{w_1+w_2}(|\vec{p_1}-\vec{p_2}|-d)\frac{\vec{p_1}-\vec{p_2}}{|\vec{p_1}-\vec{p_2}|}$$
ここで、$w=1/m$です。質量$m$が「物質の動かしずらさ」ですから、その逆数$w$は「物質の動かしやすさ」を意味するように思えますね。これらを比でとりますから、質量が小さいほど大きく動かすようにしています。
では、この移動量Δpを一般化しましょう。例えば、ある地点pよりΔpだけ移動した点での拘束$C(p+Δp)=0$であるとします。これは、一次テイラー展開より次のように表せます。これを(1)式とします。
$$C(\vec{p}+\vec{\Delta{p}})
\simeq C(\vec{p})+\nabla_\vec{p}C(\vec{p})\cdot\Delta\vec{p}=0\quad(1)$$
一方で、Δpは拘束条件Cの地点pにおける勾配に、スカラーλ倍したものとも言えるので、これは
$$\Delta\vec{p}=\lambda\nabla_\vec{p}C(\vec{p})\quad(2)$$
と表せます。これを(2)式とします。
(2)式を(1)式に代入してλを解き、それを(2)式に代入すると次の式が得られます。
$$\Delta\vec{p}=-\frac{C(\vec{p})}{|\nabla_\vec{p}C(\vec{p})|^2}\nabla_\vec{p}C(\vec{p})$$
ただし、これは単一の拘束条件しか加味されていません。一般的には、複数の拘束条件が存在するため、これを想定すると次のように表せます。
$$\Delta\vec{p}=-\frac{C(\vec{p_1},\cdots,\vec{p_n})}{\sum_{j}|\nabla_\vec{p_j}C(\vec{p_1},\cdots,\vec{p_n})|^2}\nabla_\vec{p_i}C(\vec{p_1},\cdots,\vec{p_n})$$
さらに、質量を考えてあげると以下の最終的な式を得ることができます。
$$\Delta\vec{p}=-\frac{C(\vec{p_1},\cdots,\vec{p_n})}{\sum_{j}w_j|\nabla_\vec{p_j}C(\vec{p_1},\cdots,\vec{p_n})|^2}w_i\nabla_\vec{p_i}C(\vec{p_1},\cdots,\vec{p_n})$$
アルゴリズム
ってことでとりあえず論文中のアルゴリズムを載せます。

上から順に解説していきます。とりあえず、(1)~(3)は初期化です。(4)~は大きなループです。(5)は外力を加味した速度への更新です。位置から速度を求めるPBDでは、重力などの外力を計算に入れられないためここで外力をシステムに加えます。(6)は速度を減衰させるための処理です。空気抵抗などの速度減衰を入れるために用いられます。たぶん。(7)では理想位置を求めます。理想位置は、拘束条件などを加味しないΔt秒後の位置です。(8)では、衝突の拘束条件を生成します。これは、頂点がどれくらい衝突しているかによって拘束条件が変化するため理想位置を求めてからでないと生成できません。(9)~(11)は拘束条件をもとに実際の位置を求めていきます。(12)~(15)は実際の位置から現在の速度を求めます。そして、実際の位置を次フレームで使用するために現在の位置に格納します。(16)では、衝突などによって減少した速度を反映させます。
以上がアルゴリズムの概要です。合っている保証はできません。
あとがき
なかなか難しい論文でした。しかし、様々な論文のもととなっているので少なくとも自分の力にはなったと思います。まだまだ、衝突解決の簡易性や速度減少のアルゴリズムなど、理解できていない部分もあると思うので、出来れば更新していきたいと思います。
参考:
コンピュータグラフィックスアニメーション論(2)
中川さんのPosition-Based-Dynamics-Comboのスライドを読む(その1)
中川さんのPosition-Based-Dynamics-Comboのスライドを読む(その2)
中川さんのPosition-Based-Dynamics-Comboのスライドを読む(その3)
Position Based Dynamics Combo 物理シミュレーション関連の最新論文実装