概要
水の凝固問題を等価比熱法で解き,ノイマン解(解析解)と比較する.
問題設定
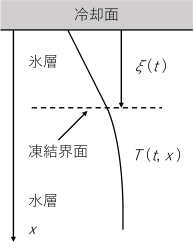
下図のような静止流体中に置かれた冷却面から氷層が1次元的に成長していく問題を考える.
冷却面から垂直方向にx軸をとり,時刻$t$ [s],位置$x$ [m]における温度を$T(t, x)$,時刻$t$における凍結界面の位置を$\xi(t)$とする.
支配方程式
潜熱放出による発熱量を考慮した1次元のエネルギー保存則は1,
\rho C_p\cfrac{\partial T}{\partial t} = \cfrac{\partial}{\partial x}\left(\lambda\cfrac{\partial T}{\partial x}\right) + \rho L\cfrac{\partial f}{\partial t}
となる.ここで,$\rho$は密度 [kg/m$^3$],$C_p$は比熱 [J/(kg$\cdot$K)]2,$\lambda$は熱伝導率 [W/(m$\cdot$K)],$L$は潜熱 [J/kg],$f$は固相率 [-]である.
等価比熱法
相変化を取り扱うための手法として,等価比熱法,エンタルピ法,温度回復法などが提案されている.
本記事では,等価比熱法を用いて相変化を取り扱うことにする.
固相率の時間変化を
\cfrac{\partial f}{\partial t} = \cfrac{\partial f}{\partial T}\cfrac{\partial T}{\partial t}
と変形し,支配方程式に代入すると,
\rho \left(C_p - L\cfrac{\partial f}{\partial T}\right)\cfrac{\partial T}{\partial t} = \cfrac{\partial}{\partial x}\left(\lambda\cfrac{\partial T}{\partial x}\right)
が得られる.今,見かけの比熱$C = C_p + L,\partial f/\partial T$とおくと,
\rho C\cfrac{\partial T}{\partial t} = \cfrac{\partial}{\partial x}\left(\lambda\cfrac{\partial T}{\partial x}\right)
となり,これは1次元の熱伝導方程式に他ならない.
つまり,等価比熱法では,比熱を見かけの比熱(等価比熱)に置き換えることによって相変化によるエネルギー変化を簡便に扱っている.
具体的には,相変化が起きている場所では,潜熱分だけ比熱を大きくして温度変化しづらくすることによって相変化を表現し,それ以外の場所では固体又は液体の比熱を使う.
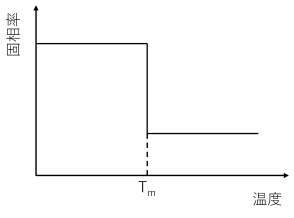
見かけの比熱について詳しく見ていくことにする.氷のように一定温度で相変化が進む物質だと,温度と固相率の関係は下図のようになり,融解温度$T_m$において固相率と温度が1対1対応でない.したがって,ある点の温度が$T_m$である時,その点は0℃の氷なのか,水なのか,相変化中で氷と水があるのかが分からず,見かけの比熱を決められないという問題が生じる.
そこで下図に示すように,混合物のように融解開始温度$T_s$と融解終了温度$T_l$を持つものとし,その間を直線で補間する3.
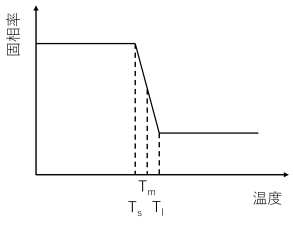
こうすることによって,温度と固相率の関係が1対1になり,温度が分かれば固相率が分かる.つまり,その点が相変化中なのか,氷なのか,水なのかが分かる.
$T_s \leq T \leq T_l$の範囲では,
T = T_l - (T_l - T_s)f
より,
\cfrac{\partial f}{\partial T} = -\cfrac{1}{T_l - T_s}
比熱$C_p$も$T_s$から$T_l$の間で氷の比熱$C_s$から水の比熱$C_l$に線形に変化すると考えると,
C_p = \left\{
\begin{array}{ll}
C_s & (T \lt T_s) \\
C_s + \cfrac{C_l - C_s}{T_l - T_s}(T - T_s) & (T_s \leq T \leq T_l) \\
C_l & (T \gt T_l)
\end{array}
\right.
となる.
以上より見かけの比熱$C$は,
C = \left\{
\begin{array}{ll}
C_s & (T \lt T_s) \\
C_s + \cfrac{C_l - C_s}{T_l - T_s}(T - T_s) + \cfrac{L}{T_l - T_s} & (T_s \leq T \leq T_l) \\
C_l & (T \gt T_l)
\end{array}
\right.
密度および熱伝導率も$\rho_s$,$\lambda_s$から$\rho_l$,$\lambda_l$へそれぞれ線形に変化すると考えると,
\rho = \left\{
\begin{array}{ll}
\rho_s & (T \lt T_s) \\
\rho_s + \cfrac{\rho_l - \rho_s}{T_l - T_s}(T - T_s) & (T_s \leq T \leq T_l) \\
\rho_l & (T \gt T_l)
\end{array}
\right.
\lambda = \left\{
\begin{array}{ll}
\lambda_s & (T \lt T_s) \\
\lambda_s + \cfrac{\lambda_l - \lambda_s}{T_l - T_s}(T - T_s) & (T_s \leq T \leq T_l) \\
\lambda_l & (T \gt T_l)
\end{array}
\right.
となる.
差分法による実装
導出した式をもう一度示す.
\rho C\cfrac{\partial T}{\partial t} = \cfrac{\partial}{\partial x}\left(\lambda\cfrac{\partial T}{\partial x}\right)
C = \left\{
\begin{array}{ll}
C_s & (T \lt T_s) \\
C_s + \cfrac{C_l - C_s}{T_l - T_s}(T - T_s) + \cfrac{L}{T_l - T_s} & (T_s \leq T \leq T_l) \\
C_l & (T \gt T_l)
\end{array}
\right.
\rho = \left\{
\begin{array}{ll}
\rho_s & (T \lt T_s) \\
\rho_s + \cfrac{\rho_l - \rho_s}{T_l - T_s}(T - T_s) & (T_s \leq T \leq T_l) \\
\rho_l & (T \gt T_l)
\end{array}
\right.
\lambda = \left\{
\begin{array}{ll}
\lambda_s & (T \lt T_s) \\
\lambda_s + \cfrac{\lambda_l - \lambda_s}{T_l - T_s}(T - T_s) & (T_s \leq T \leq T_l) \\
\lambda_l & (T \gt T_l)
\end{array}
\right.
これを差分法によって離散化する.
詳細は割愛するが,熱伝導率が場所の関数であることに注意して離散化していくと次のようになる.
\rho_i C_i \cfrac{T_i^{n+1} - T_i^n}{\Delta T} = \cfrac{1}{2\Delta x^2}\left((\lambda_{i+1} + \lambda_i)T_{i+1}^n - (\lambda_{i+1} + 2\lambda_{i} + \lambda_{i-1})T_i^n + (\lambda_i + \lambda_{i-1})T_{i-1}^n \right)
ここで,添字$i, n$はそれぞれ格子番号,時刻,$\Delta x$は格子幅をあらわす.これより,
T_i^{n+1} = T_i^n + \cfrac{\Delta t}{2\rho_i C_i \Delta x^2}\left((\lambda_{i+1} + \lambda_i)T_{i+1}^n - (\lambda_{i+1} + 2\lambda_{i} + \lambda_{i-1})T_i^n + (\lambda_i + \lambda_{i-1})T_{i-1}^n \right)
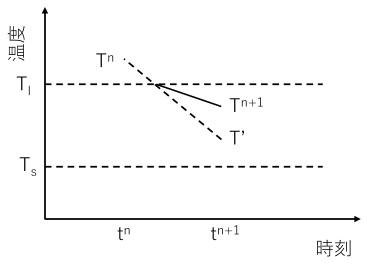
ただし,$T^n$から$T^{n+1}$の間に$T_s$または$T_l$をまたぐ場合は次の時刻の温度を過大/過小評価してしまうため,次に示すような補正が必要である.
いま,上図のように時刻$n+1$の温度$T'$を仮に求めると,時刻$n$から$n+1$の間に温度が低下し,$T_l$をまたいでいたとする.補正後の温度$T^{n+1}$は,
\rho C(T^n - T') = \rho C_p(T^n - T_l) + \rho C(T_l - T^{n+1})
という,補正前後で単位体積当たりの熱量が変化しないという条件より,
T^{n+1} = T_l - (T_l - T')C_p/C
と補正することができる.同様に$T_s$をまたぐ場合,温度が上昇する場合を考える必要があるがここでは省略する.
ノイマン解(解析解)との比較
10℃の水を容器に入れ,容器底面を$T_w = -15$ ℃に保って底面から凍結させる.水の密度変化による自然対流の影響は考慮しないものとする.
物性値は以下のとおりである.
\lambda_s = 2.19\ {\rm W/(m\cdot K)},\ \lambda_l = 0.576\ {\rm W/(m\cdot K)}\\
\rho_s = 9.17 \times 10^2\ {\rm kg/m^3},\ \rho_l = 1.0 \times 10^3\ {\rm kg/m^3}\\
C_s = 2.04\ {\rm kJ/(kg\cdot K)},\ C_l = 4.2\ {\rm kJ/(kg\cdot K)}\\
L = 334.0\ {\rm kJ/kg}\\
T_m = 0\ {\rm ^\circ C}
このとき,時刻$t$における凍結層厚さ$\xi(t)$は,
\xi(t) = 4.07 \times 10^{-4}\sqrt{t}
と解析的に求められる4.
この問題を等価比熱法を用いて解いてみる.
計算領域$L = 0.1$ m,格子分割数256,時間刻み幅$\Delta t = 1.0 \times 10^{-3}$ s,$T_s = T_m - 0.01$,$T_l = T_m + 0.01$.
境界条件は$x = 0$で$T = T_w$のディリクレ条件,$x = L$で$\partial T/\partial x = 0$のノイマン条件を与える.
初期条件は計算領域全域で$T = 10$ ℃とする.
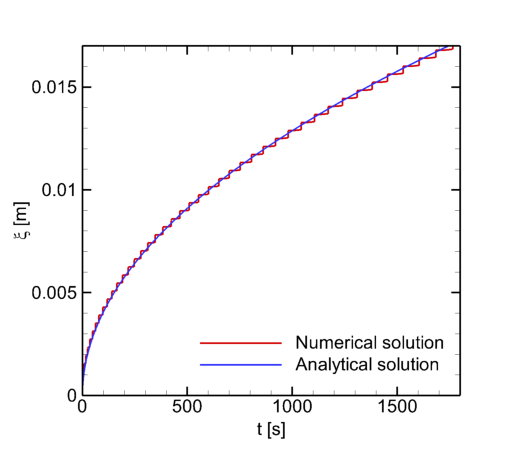
計算結果は以下のとおりである.
多少ギザギザしているが,大体解析解と合っていることが分かる.
なお,本計算の範囲では,温度補正の有無による差はほとんど見られなかった.
まとめ
等価比熱法を用いて水の凝固問題を解き,解析解と比較した.
等価比熱法は簡便な方法だが,相変化を取り扱うことができる.