はじめに
前回、生成AIを用いてScaling Lawsの論文「Scaling Laws for Autoregressive Generative Modeling (2020)」の内容(本文)を(なるべく)把握してみました。
同論文の末尾にあるAppendixについても、前回と同様の方法で、把握してみます。
E章の、相互情報量、InfoGain、訓練データ分布間のKLダイバージェンス、等の部分については、よく分からなかった。(その他、末尾の「分かったこと」章を参照)
以降で、ChatGPTに聞いてみた例を記載します。
前回の記事: (本文の内容)
対象の論文
論文: (Scaling Lawsに関する論文)
[2010.14701] Scaling Laws for Autoregressive Generative Modeling
https://arxiv.org/abs/2010.14701
(PDF: https://arxiv.org/pdf/2010.14701)
質問時の各章節の区切り部分
論文の中にある各章節を、下記のように区切って、部分毎に生成AIに内容を質問していきます。
- A More Details on Image Modeling
- ---
- B Details of Math Experiments and Additional Results
- B.1 Procedurally Generated Training Data
- ---
- B.2 Dataset Size Scaling
- B.3 Additional Math Results
- ---
- C Additional Multimodal Results
- ---
- D Additional Language Results
- ---
- E Mutual Information, Infogain, and Scaling
- ---
- E.1 Approximate Derivation of Scaling Relations
- ---
- E.2 Estimating DKL Between Real-World Distributions
- ---
- F Hyperparameter Settings
生成AIへの質問方法
生成AIを活用して、知りたい記事・論文の1節分(適度な長さ)のテキストをコピー&ペーストして、その下に質問内容を「①~ ②~ …」と番号付きで書いて、生成AIに渡せば、全質問に一発で的確に回答してくれるので、非常に良好でした。記事全体を読む必要なく、知りたい点の情報だけを収集できます。
生成AIへの質問例:
(論文・記事の各章節を貼り付け)
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑤性能が向上した記載があれば説明下さい。(具体値があれば記載、対応する図/表番号があれば各文末に記載)
続けて下記の質問に追加で回答下さい:
⑥比較の記載があれば違いを表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば明記)
⑦上記⑥以外で表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑧具体的な数値の記載を全て列挙して、表にまとめて下さい。(必ず正しく数値を抜き取る事、|数値|説明|の表へ)
⑨具体的な変数名(数式用の記号)の記載を全て列挙して、表にまとめて下さい。(|変数名|説明|次元・型|の表へ)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
※回答が長くなりそうな場合は、適宜、分けて質問: ①②③④⑤、⑥⑦⑧⑨⑩
※各章節に応じて、その章節内で明らかに不要な質問は、適宜除外。
※各章節に応じて、適宜下記の質問を追加。
⑪関連研究の参照番号を全て列挙して、表にまとめて下さい。(元文にある内容のみ記載・類推して付け足しは不要、|参照番号|概要説明|の表へ、関連するもの同士でまとめて並べ替え)
⑫難解用語を全て列挙して、表にまとめて下さい。(必ず正しく抜き取る事、|用語|説明|の表へ)
※その他、不明点があれば、適宜、ピンポイントで質問。
質問内容は、記事・論文を読んでいていつも知りたいと思う点(改良点・工夫点・テクニック・メカニズムの解明)にしています。また、表で比較した方が素早く把握できるので、可能であれば記事を表に変換するようにしています。
論文・記事を貼り付けるテキストの長さは、1節分程度の量にとどめた方が、良い回答が得られました。生成AIの回答の文量が多くなってくると、回答が長くなり過ぎないように、生成AIが勝手に(適度に)端折り始めてしまい、重要な点が回答から抜けてしまう可能性が高くなります。
事前知識
機械学習についてある程度知っていないと、生成AIに質問しても、その回答内容だけでは理解できないと思います。生成AIの回答は、論文の内容をあまり変えずに、要点をそのまま掻い摘んで回答するような形になっています。
Scaling Lawsの論文についての分かりやすい解説記事(下記)等を事前にチェックして、中核部分の内容をあらかじめ分かっていると、理解しやすいと思います。生成AIは実際の細かい処理方法自体を分かりやすく説明してはくれない傾向があります。
注意点
論文のテキスト内容だけを貼り付けて、生成AIに質問しています。論文の中の図・表の部分は貼り付けていません。図・表の内容は生成AIの回答には含まれず、別途論文を見る必要があります。
以降で、生成AIの回答内容が読みにくい・分かりづらい場合は、論文の本文でも同じように書かれてあり、論文の本文を読んでも同じように分かりづらいことが多くあります。論文では、既存研究等があるため、多くの説明を省略・一言だけサラッと書かれてある等、同種の研究に取り組む人でなければ、なかなか全容の理解に辿りつくのは難しい側面があります。この点は、生成AIの回答性能が悪いのではなく、論文という性質上、生じるものと考えています。
生成AIに質問
以降で、ChatGPTに実際に聞いてみた例を記載します。
生成AIへの質問&回答の全容
生成AIへの質問&回答の全容・詳細:
A More Details on Image Modeling
▼質問(人間)
質問内容全体はここをクリック
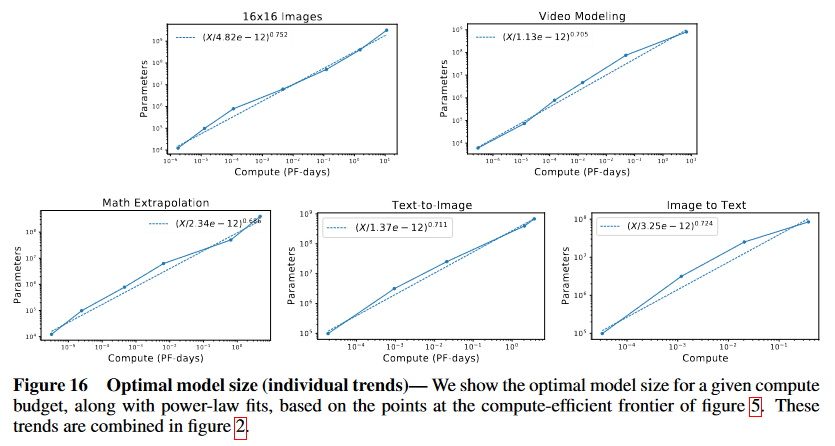
(論文・記事の各章節を貼り付け) A More Details on Image Modeling In figures 18 and 19 we provide some additional information documenting compute scaling trends for images with different resolutions and encodings. In figure 20 we show images where the loss improved most or least as we pass from a 100k parameter model to a 400M parameter model. In figure 17 we also show trends for randomly selected individual images from the test set.Figure 16 Optimal model size (individual trends)— We show the optimal model size for a given compute
budget, along with power-law fits, based on the points at the compute-efficient frontier of figure 5. These
trends are combined in figure 2.
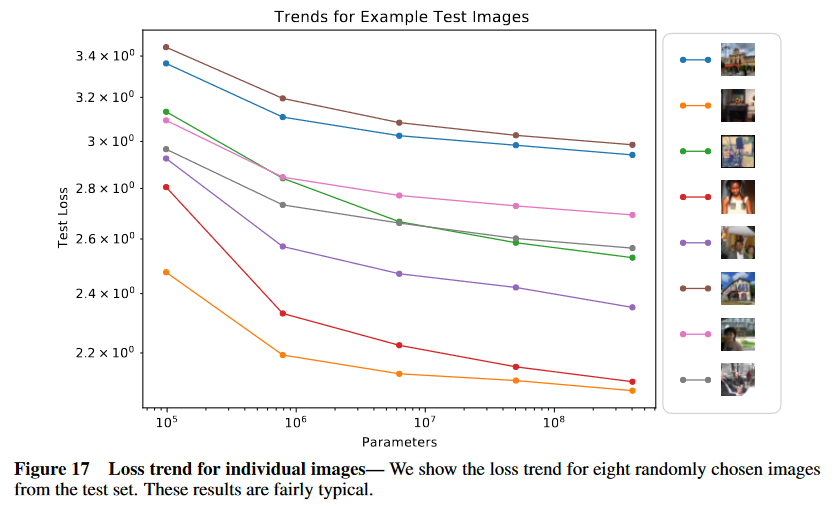
Figure 17 Loss trend for individual images— We show the loss trend for eight randomly chosen images
from the test set. These results are fairly typical.
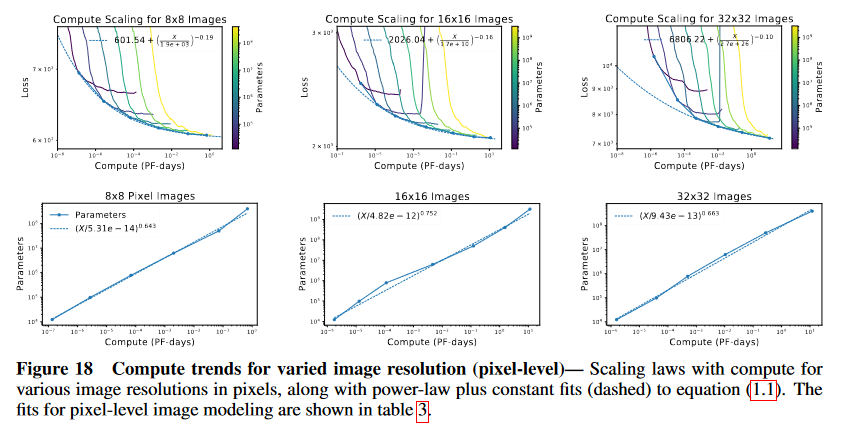
Figure 18 Compute trends for varied image resolution (pixel-level)— Scaling laws with compute for
various image resolutions in pixels, along with power-law plus constant fits (dashed) to equation (1.1). The
fits for pixel-level image modeling are shown in table 3.
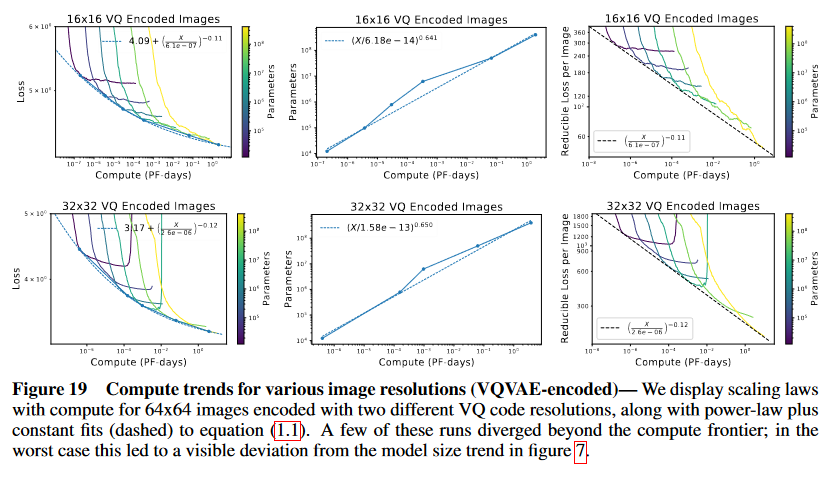
Figure 19 Compute trends for various image resolutions (VQVAE-encoded)— We display scaling laws
with compute for 64x64 images encoded with two different VQ code resolutions, along with power-law plus
constant fits (dashed) to equation (1.1). A few of these runs diverged beyond the compute frontier; in the
worst case this led to a visible deviation from the model size trend in figure 7.
Figure 20 Most and least improved images— Here we show the images where the loss improved most
or least between models with 400M parameters and 100k parameters. These were the ten most or least
improved images from a random sample of one thousand images in the test set, as measured by loss ratio
and loss difference. Images with complex colorful scenes involving people or crowds are typically most
improved, while black and white images and those dominated by a simple background tend to be the least
improved.
Figure 21 Trends in image completion quality— Here we show conditional-completions of 32x32 pixel
models of various sizes, where the leftmost column is the original image, and each of the other columns shows
completions from a model with a non-embedding parameter count labeled at the top. Models are provided
the top half of the image as conditional context and the bottom half is sampled with temperature 1.0. There
is a clear trend of increasing photorealism with larger models.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑤性能が向上した記載があれば説明下さい。(具体値があれば記載、対応する図/表番号があれば各文末に記載)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
この部分では、画像モデリングにおける計算量のスケーリング法則と、異なるモデルサイズや画像解像度に基づく性能のトレンドが示されている。具体的には、異なるパラメータ数のモデルによる損失改善や、個々の画像に対する損失の変化、最適なモデルサイズの検証結果などについて記載されている。
要旨
- 図18および19では、異なる解像度およびエンコーディングを持つ画像に対する計算量のスケーリングトレンドを示している。
- 図20では、100kパラメータモデルから400Mパラメータモデルに移行した際に、最も損失が改善された画像と最も改善されなかった画像が提示されている。
- 図17では、テストセットからランダムに選ばれた個々の画像の損失トレンドが示されている。
- 図16では、特定の計算予算に対する最適なモデルサイズが、計算効率のフロンティアに基づいて示されている。
- 図21では、異なるモデルサイズでの画像補完の品質が比較されており、モデルサイズが大きくなるにつれて、フォトリアリズムが向上している。
②具体的な処理方法の記載
-
図18および図19での画像のスケーリングトレンドに関しては、ピクセルレベルおよびVQ-VAEエンコードされた画像の異なる解像度に対して計算量のスケーリング法則を適用しており、これにはパワーロー(べき乗則)に基づく近似式が使用されている (式1.1)。
- ピクセルレベルの画像モデリングのフィットは表3に示されている。
- VQVAEエンコードされた64x64の画像については、異なるVQコード解像度を用いたモデルを試し、パワーローと定数項のフィット(破線)を適用した。
- 一部のランが計算フロンティアを超えて発散し、最悪の場合、図7のモデルサイズトレンドからの逸脱が見られる。
-
図20では、100kパラメータモデルと400Mパラメータモデル間で損失が最も改善された画像と、最も改善されなかった画像が提示されている。ランダムに選ばれたテストセットの1000枚の画像のうち、損失比および損失差で最も改善された10枚の画像と、最も改善されなかった10枚の画像が示されている。
-
図21では、32x32ピクセルの画像モデルにおける条件付き補完が実行されており、元画像の上半分を条件として提供し、下半分を温度1.0でサンプリングした結果が示されている。モデルサイズが増加するにつれて、生成された画像のフォトリアリズムが向上している。
③改良点・工夫点・テクニック等の記載
- 画像の解像度と計算量のスケーリングに関しては、パワーローに基づくフィット(式1.1)を使用して、計算量の効率化を図っている (図18, 19)。
- VQVAEエンコーディングを使用した画像では、異なるVQコード解像度を試し、より高い精度のエンコーディングが性能向上に寄与している。
- モデルサイズの最適化に関しては、特定の計算予算に対して、計算効率のフロンティアに基づく最適なモデルサイズを提示している (図16)。
④メカニズムの解明・なぜそうなるのか等の記載
- モデルサイズが大きくなると、より高次の特徴を捉えることが可能となり、これにより画像のフォトリアリズムや損失の改善が見られる (図20, 図21)。特に、複雑なカラフルなシーンや人間・群衆を含む画像では、損失の大幅な改善が確認されている。
- 逆に、単純な背景や白黒画像に対しては、損失の改善が最も少なく、モデルサイズの増加があまり影響を与えないことが示されている (図20)。
⑤性能が向上した記載
- 図20では、複雑でカラフルなシーンや人々が含まれる画像では、100kパラメータモデルから400Mパラメータモデルに移行することで、損失が大幅に改善された。
- 図21では、モデルのパラメータ数が増加するにつれて、32x32ピクセルの画像の条件付き補完におけるフォトリアリズムが明らかに向上していることが示されている。
- 図16では、計算効率のフロンティアに基づく最適なモデルサイズが示されており、これによりパラメータ数と計算リソースのバランスが取れている。
▼質問(人間)
続けて下記の質問に追加で回答下さい:
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
▼生成AIの回答(ChatGPT-4o)
⑥表に出来そうな部分
| 図/表番号 | 変更点・特徴 | 主な内容 | 結果や注目点 |
|---|---|---|---|
| 図16 | 最適なモデルサイズのトレンド | 計算予算に対して最適なモデルサイズを示す | 計算効率のフロンティアに基づき、最適なモデルサイズが特定されている |
| 図17 | 個別画像に対する損失トレンド | テストセットからランダムに選ばれた8枚の画像の損失トレンド | 個別画像に対する典型的な損失トレンドを示している |
| 図18 | ピクセルレベル画像の解像度ごとの計算トレンド | ピクセルレベルの画像モデリングにおけるスケーリング法則 | パワーロー近似式を使用したスケーリングトレンドが表3に示されている |
| 図19 | VQVAEエンコードされた画像の計算トレンド | VQVAEでエンコードされた64x64画像のスケーリング法則 | 一部ランが計算フロンティアを超え、モデルサイズトレンドからの逸脱が確認される |
| 図20 | 損失が最も改善された/されなかった画像 | 100kパラメータモデルと400Mパラメータモデル間での損失改善 | 複雑でカラフルなシーンの画像が最も改善され、単純な背景の画像は改善が少ない |
| 図21 | 画像補完のフォトリアリズムのトレンド | モデルサイズによる画像補完の品質比較 | モデルサイズが増加するにつれてフォトリアリズムが向上する |
- 解説: この表は、各図/表において示されている特徴や結果を整理したものである。特に、計算効率のフロンティアに基づく最適なモデルサイズ(図16)、個別の画像に対する損失トレンド(図17)、解像度別の計算トレンド(図18, 19)、損失改善の差(図20)、および画像補完の品質比較(図21)が重要な要素として提示されている。
⑩図/表があれば、各図/表は何を主張するためのものかを説明
-
図16 (Optimal model size): 計算予算に対して最適なモデルサイズのトレンドを示している。この図は、計算効率のフロンティア(図5)に基づいており、限られた計算リソース内で最大の性能を発揮するためにどのモデルサイズが適しているかを示している。ポイントとしては、パワーローのフィットを利用して計算予算に応じた最適なモデルサイズが導き出されている点に注目。
-
図17 (Loss trend for individual images): テストセットからランダムに選ばれた8つの画像の損失トレンドを示しており、典型的な損失の挙動が観察される。この図は、個々の画像が異なる損失挙動を示すことを視覚化し、一般的なトレンドを理解するために役立つ。
-
図18 (Compute trends for varied image resolution - pixel-level): 異なる画像解像度における計算量のスケーリングトレンドを示している。ピクセルレベルの画像モデリングにおいて、パワーローのフィットを用いることで、解像度と計算量の関係が表されている。表3にフィット結果が示されているが、この図は解像度に応じた計算効率の向上を評価するための重要なデータを提供している。
-
図19 (Compute trends for VQVAE-encoded images): VQVAEエンコードされた64x64ピクセルの画像におけるスケーリングトレンドを示している。VQコード解像度の違いに基づいて計算効率を評価しており、一部のランが計算フロンティアを超えたことで、モデルサイズのトレンドから逸脱する場合があることが指摘されている。
-
図20 (Most and least improved images): 100kパラメータモデルから400Mパラメータモデルへの移行時に、損失が最も改善された画像と改善が少なかった画像を示している。複雑でカラフルなシーンの画像が最も改善され、単純な背景の画像は改善が少ないという傾向が確認されている。この図は、モデルサイズの違いがどのように画像の損失改善に影響を与えるかを視覚的に示している。
-
図21 (Trends in image completion quality): 32x32ピクセルの画像補完におけるモデルサイズの影響を示している。モデルサイズが増加するにつれて、生成される画像のフォトリアリズムが向上するトレンドが明確に確認できる。この図は、モデルのスケーラビリティと性能の向上を視覚的に示すために用いられており、大規模モデルの優位性が強調されている。
B Details of Math Experiments and Additional Results
B.1 Procedurally Generated Training Data
▼質問(人間)
質問内容全体はここをクリック
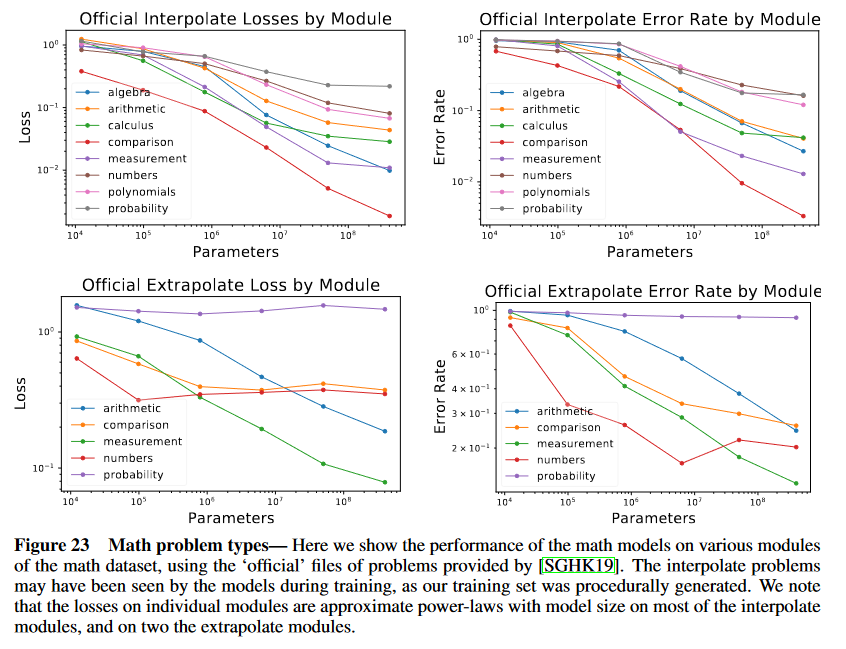
(論文・記事の各章節を貼り付け) B Details of Math Experiments and Additional Results B.1 Procedurally Generated Training Data We generated all training data procedurally using the code provided by [SGHK19]. Problems were generated by randomly sampling modules from the training distribution, with an ‘entropy’ setting sampled uniformly from the integers s ∈ [3, 10]. The number of problems with entropy s is approximately 10s, meaning that easy problems with low-entropy would likely be seen by the model many, many times, while some problems with s ≥ 9 may not be seen at all. This means that the easy components of the training distribution may be memorized. Furthermore, our procedurally generated data was not deduplicated from the ‘interpolate’ test distribution [SGHK19], but it is completely disjoint from the ‘extrapolate’ test distribution. The official extrapolate distribution only provides one difficulty level, and it also does not include all eight module-types. So we also generated distributions of problems with smoothly increasing difficulty level by setting the entropy s = 1, 2, · · · 19. For most modules we simply used the interpolate set- tings, though for modules where other parameters were needed we generally used the extrapolation set- tings. Importantly, we did not include the probability__swr_p_level_set_more_samples and probabil- ity__swr_p_sequence_more_samples generators, as we found our models always performed poorly on these problems, and quickly overfit on the loss for these generators (this can be seen in figure 23, where ‘probability’ represents the mean of these two generators). Performance as a function of difficulty level and model size can be seen in figure 24. We note that performance degrades smoothly as we extrapolate away from the training distribution. As an additional note, because these experiments were conducted much earlier, our dataset size scaling and aspect ratio scans use models with the fairly standard setting mmlp = 4 and mattn = 1, as with language and multimodal models, but different from the math models we used for compute and model size trends, where these parameters were smaller by a factor of 4, as with our image and video models. We made this change to smaller mmlp, mattn as we found it helped to improve the training stability of very deep math models. It is also worth noting that we evaluated extrapolation performance both using the training data files provided with [SGHK19] and by sampling with procedurally generated data (leaving out the two probability modules previously discussed). For trend plots we have used the procedurally generated data, but for reporting final accuracies in figure 26 we use the ‘official’ files.Figure 23 Math problem types— Here we show the performance of the math models on various modules
of the math dataset, using the ‘official’ files of problems provided by [SGHK19]. The interpolate problems
may have been seen by the models during training, as our training set was procedurally generated. We note
that the losses on individual modules are approximate power-laws with model size on most of the interpolate
modules, and on two the extrapolate modules.
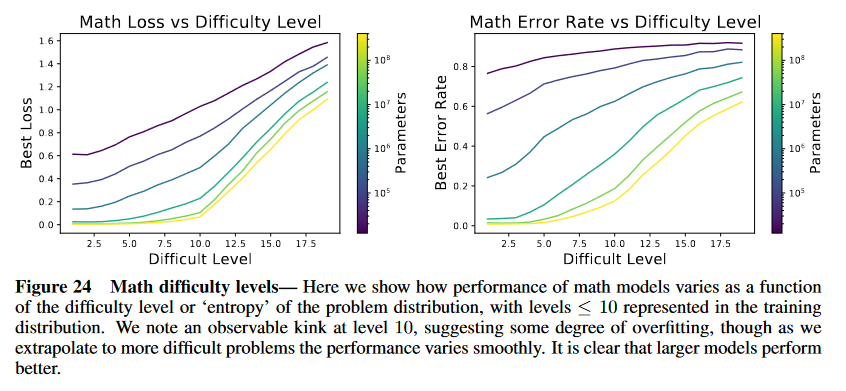
Figure 24 Math difficulty levels— Here we show how performance of math models varies as a function
of the difficulty level or ‘entropy’ of the problem distribution, with levels ≤ 10 represented in the training
distribution. We note an observable kink at level 10, suggesting some degree of overfitting, though as we
extrapolate to more difficult problems the performance varies smoothly. It is clear that larger models perform
better.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
この節は、数式問題を扱うモデルの実験と結果に関する詳細を説明している。特に、訓練データの生成方法やモデルの性能に影響を与える要因が中心となっている。
- 訓練データは、[SGHK19]のコードを使用して手続き的に生成された。
- 問題の難易度は「エントロピー」$ s \in [3, 10] $ で定義され、低エントロピーの問題はモデルによって多く見られる一方、高エントロピーの問題はほとんど見られない可能性がある。
- 訓練データは「interpolate」テストセットと重複しているが、「extrapolate」テストセットとは完全に異なるものである。
- 数学モデルは、訓練セットで見られる難易度レベル(エントロピー10以下)では比較的良い性能を示すが、より難しい問題(エントロピーが11以上)に対しては性能が徐々に低下する傾向がある。
- 実験では、特定のモジュールやジェネレータにおいて、モデルが急速に過学習することが観察された(図23参照)。
- データセットのスケーリングとアスペクト比のスキャンは、言語やマルチモーダルモデルと同様の設定で行われたが、数学モデルでは異なる設定が使用された。
②具体的な処理方法の記載
- 訓練データは手続き的に生成された。これには、[SGHK19]のコードを使用し、ランダムにモジュールをサンプリングして問題を生成するという方法が取られた。問題のエントロピー$ s $は、整数範囲$ s \in [3, 10] $ から一様にサンプリングされた。
- 各エントロピーに対応する問題の数は $ 10^s $ であり、エントロピーが低い問題は頻繁に登場し、エントロピーが高い問題($ s \geq 9 $)は訓練セットに登場しない可能性がある。
- 手続き的に生成されたデータは、「interpolate」テストセットとは重複しているが、「extrapolate」テストセットとは完全に異なるデータであった。
- 図23に示されているように、「probability__swr_p_level_set_more_samples」と「probability__swr_p_sequence_more_samples」ジェネレータは、モデルが過学習する傾向が強く、それらを除外してトレーニングが行われた。
- エントロピーが1から19までの問題を生成するため、難易度レベルが徐々に増加するように設定され、ほとんどのモジュールでは「interpolate」設定が使用された。
- 結果の報告にあたり、トレンドプロットには手続き的に生成されたデータが使用されたが、最終的な精度報告には[SGHK19]の公式ファイルが使用された。
③改良点・工夫点・テクニック等の記載
- 訓練データの生成において、エントロピー$ s $を1から19まで設定し、問題の難易度が滑らかに増加するように工夫されている。
- 訓練の安定性を向上させるために、画像やビデオモデルで使用されるパラメータ設定を数学モデル用に縮小し、具体的には $ mmlp $と $ mattn $ の値をそれぞれ4分の1に減少させた。この調整により、非常に深い数学モデルの訓練がより安定化した。
- モジュールごとに異なるジェネレータを使用することで、特定の問題に対する過学習のリスクを減らすための工夫がなされた。また、過学習しやすいジェネレータを除外することが、モデルの性能向上に寄与している。
④メカニズムの解明・なぜそうなるのか等の記載
- 訓練セットに多く出現する低エントロピーの問題は、モデルによって「記憶される」可能性が高い一方、高エントロピーの問題は訓練セットにほとんど含まれないため、これらの問題に対するモデルのパフォーマンスは一般に低下する。このメカニズムは、訓練データのエントロピー分布によってパフォーマンスが左右されることを示唆している。
- 非常に深い数学モデルにおいては、$ mmlp $ と $ mattn $ の値を小さくすることで、過度に複雑なモデルの訓練が安定化し、結果としてより高い性能が得られるようになった。
⑥表に出来そうな部分
| 図/表番号 | 説明 | 主な内容 | 結果・注目点 |
|---|---|---|---|
| 図23 | 数学問題のモジュールの性能 | [SGHK19]が提供する公式ファイルに基づく問題に対する性能 | 「interpolate」問題での損失は、モデルサイズに応じたパワーローの関係を示す |
| 図24 | 数学問題の難易度と性能の関係 | 問題のエントロピーに応じたモデルの性能 | エントロピーが10以下の問題での過学習が観察され、難易度が上がると性能が徐々に低下する |
- 解説: この表は、数式モデルの実験における結果を簡潔にまとめたものである。特に、図23ではモジュールごとの性能が示され、図24では問題の難易度(エントロピー)に応じたモデルの性能が強調されている。
⑩図/表があれば、各図/表は何を主張するためのものかを説明
-
図23 (Math problem types): この図は、数学モデルが異なるモジュールに対してどの程度の性能を発揮するかを示している。特に、公式に提供された問題ファイルに基づいている点が重要であり、「interpolate」問題の一部はモデルが訓練中に見た可能性がある。この図の主張ポイントは、モジュールごとの損失がモデルサイズに対してパワーローの関係にあることである。
-
図24 (Math difficulty levels): この図は、問題の難易度(エントロピー)とモデルの性能との関係を示している。難易度が低い問題(エントロピー10以下)では性能が高いが、難易度が上がると性能が徐々に低下する傾向が見られる。特に、エントロピーが10のところで一種の「キンク」(急な変化)が確認されており、これは過学習の兆候を示している。この図の主張は、問題の難易度がモデルの性能に与える影響を視覚的に示すことである。
B.2 Dataset Size Scaling
B.3 Additional Math Results
▼質問(人間)
質問内容全体はここをクリック
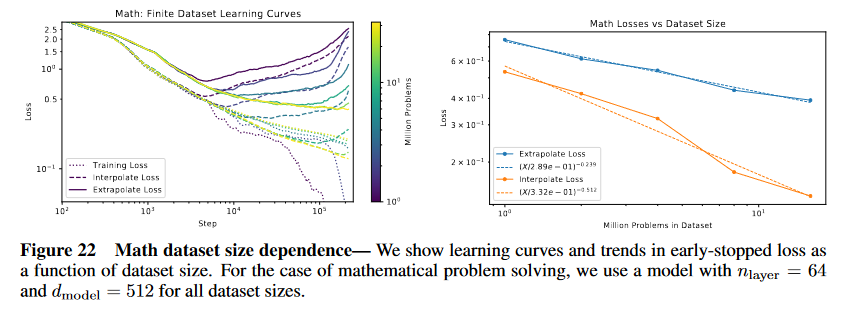
(論文・記事の各章節を貼り付け) B.2 Dataset Size Scaling For the math dataset we studied optimal performance as a function of dataset size D, in the limit where N >> D so that performance is constrained by overfitting rather than by model size or compute budget. For each dataset size and problem distribution, we define L(D) by taking the minimum loss during training (this differs slightly from early stopping, since we may evaluate at different steps if there are several metrics, ie losses on different test distributions, as is the case for math). For these experiments we used models with nlayer = 64 and dmodel = 512 for all dataset sizes. We obtain power-law fits for L(D), as shown in figure 22. B.3 Additional Math Results Here we provide several additional observations about math performance, which can be divided among dif- ferent math modules and difficulty levels. In figure 23 we show performance on different modules (using the files provided in [SGHK19]), while in figure 24 we show performance as a function of difficulty level for dif- ferent model sizes. We provide details of achieved accuracies on the official extrapolation and interpolation test sets in figures 26 and 27.Figure 22 Math dataset size dependence— We show learning curves and trends in early-stopped loss as
a function of dataset size. For the case of mathematical problem solving, we use a model with nlayer = 64
and dmodel = 512 for all dataset sizes.
Figure 25 Model size trends for math difficulty levels— These plots show trends for the official interpo-
late dataset, as well as several difficulty levels that are within the training distribution. We observe that the
power-law trends are distorted, perhaps as a consequence of memorization and the implicit curriculum in the
data distribution.
Figure 26 Extrapolation results for all math problem types— Here we show accuracies achieved by
models of three different sizes on the official extrapolation test set files from [SGHK19], grouped by problem
generator. Performance almost always improves with model size, though as shown in figure 13, this is due to
the fact that larger models achieve better training loss.
Figure 27 Interpolation results for all math problem types— Here we show interpolation accuracies
achieved by a 400M parameter model, by problem generator. Note that these problems (files from [SGHK19])
were not deduplicated from our procedurally generated training set, so they may be contaminated by memo-
rization.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
-
B.2 Dataset Size Scaling: 数学データセットにおけるデータセットサイズ $D$ とパフォーマンスの関係についての記載である。この節では、データセットサイズが増加することでモデルの性能がどう変化するか、特にオーバーフィッティングに制約される状況での学習損失の挙動が議論されている。具体的には、データセットサイズごとの最小損失 $L(D)$ がパワー法則に従うことが述べられている。
- 学習データセットのサイズ $D$ と性能の関係を調査し、特に $N \gg D$ の条件下でオーバーフィッティングに制約される状況を扱う。
- データセットサイズごとの最小損失 $L(D)$ を計算し、パワー法則に従うことを確認。
- 図22では、このデータセットサイズに対する学習曲線と損失の変動が示されている。
-
B.3 Additional Math Results: 数学モジュールや難易度レベルに応じた追加のパフォーマンス結果に関する観察が提供されている。特に、図23では異なるモジュールでのパフォーマンスが、図24では難易度レベルとモデルサイズに応じたパフォーマンスが示されている。
- 図23: 異なる数学モジュールのパフォーマンスを公式の問題ファイルを用いて評価。
- 図24: モデルサイズと難易度レベルに応じたパフォーマンスの変動を示し、難易度が高い問題ほどパフォーマンスが低下する傾向を観察。
- 図26および図27: 数学問題の補間(interpolation)と外挿(extrapolation)テストセットでの精度を報告。
②具体的な処理方法の記載
-
B.2 Dataset Size Scaling:
- データセットサイズ $D$ に応じたパフォーマンスを評価する際に、すべてのデータセットサイズで使用されたモデルの構造は固定されており、具体的には $n_{layer} = 64$, $d_{model} = 512$ である。
- 最小損失 $L(D)$ は、トレーニング中の損失の最小値を評価することで決定され、いくつかのメトリクス(異なるテスト分布での損失)を用いる場合、トレーニングのステップごとに評価される。
- 損失とデータセットサイズの関係はパワー法則に従うことが確認されており、図22でその学習曲線が示されている。
-
B.3 Additional Math Results:
- 各数学モジュールのパフォーマンスを図23で示す際には、[SGHK19]で提供された公式ファイルを使用。
- 図24では、難易度レベル $s$ とモデルサイズに応じたパフォーマンスが評価されており、モデルのパラメータは補間(interpolation)テストセットに対して評価される。
- 図26および図27では、公式外挿(extrapolation)テストセットおよび補間テストセットにおける精度が異なるサイズのモデルに対して報告されている。
③改良点・工夫点・テクニック等の記載
-
B.2 Dataset Size Scaling:
- オーバーフィッティングを制約条件とした状態で、最小損失 $L(D)$ を評価するため、いくつかの異なる損失メトリクスを使用し、トレーニングステップごとに異なるタイミングで損失を評価する点が工夫されている。
-
B.3 Additional Math Results:
- 数学モジュールに対する異なるアプローチでの評価を行っており、特に外挿(extrapolation)問題ではより大きなモデルがパフォーマンス向上に貢献していることが示されている。
- 公式テストファイルと生成された問題データを比較して評価するアプローチが採用されている点も重要な工夫といえる。
④メカニズムの解明・なぜそうなるのか等の記載
-
B.2 Dataset Size Scaling:
- 学習データセットサイズが小さい場合、モデルはオーバーフィッティングに陥りやすく、その結果、トレーニング中の損失が安定しないため、パフォーマンスがデータセットサイズ $D$ に依存することが観察される。特に、損失 $L(D)$ がパワー法則に従うのは、モデルがデータセット全体を効率的に学習し、過剰にフィッティングしていることが原因であると考えられる。
-
B.3 Additional Math Results:
- モジュールごとのパフォーマンスにおいて、補間問題(interpolation)はトレーニングセットに含まれる可能性があるため、モデルがこれらの問題に対して過剰に適応している可能性がある。逆に、外挿問題(extrapolation)はトレーニングセットに含まれていないため、パフォーマンスがトレーニングセットからの距離(難易度)に応じて滑らかに変動する。
⑥表に出来そうな部分
| 項目 | 内容 | 図/表番号 |
|---|---|---|
| データセットサイズ | $n_{layer} = 64$, $d_{model} = 512$ で統一されたモデルを使用 | 図22 |
| パフォーマンス評価 | $L(D)$(トレーニング中の最小損失)をパワー法則に基づいて評価 | 図22 |
| 数学モジュール | 各モジュールのパフォーマンスが公式ファイルに基づいて評価されている | 図23 |
| 難易度レベルとパフォーマンス | 難易度レベル $s$ に応じたパフォーマンスの変動が示され、特に大規模モデルが高難易度問題で優れている | 図24 |
⑩図/表があれば、各図/表は何を主張するためのものか
-
図22 Math dataset size dependence: この図は、データセットサイズに応じた学習曲線と、トレーニングの損失の変動を示している。学習損失はデータセットサイズ $D$ に応じてパワー法則に従うことが観察され、特にオーバーフィッティングに制約される場合の挙動が確認されている。
-
図23 Math problem types: この図は、異なる数学モジュールに対するモデルのパフォーマンスを示している。公式の問題ファイルを用いた評価で、トレーニングセットに含まれている可能性がある補間問題でのパフォーマンスが観察されている。
-
図24 Math difficulty levels: この図は、難易度レベルとモデルサイズに応じた数学問題に対するパフォーマンスの変動を示している。難易度レベルが上がるほど、モデルのパフォーマンスが低下するが、大規模モデルはより高いパフォーマンスを維持している。
C Additional Multimodal Results
▼質問(人間)
質問内容全体はここをクリック
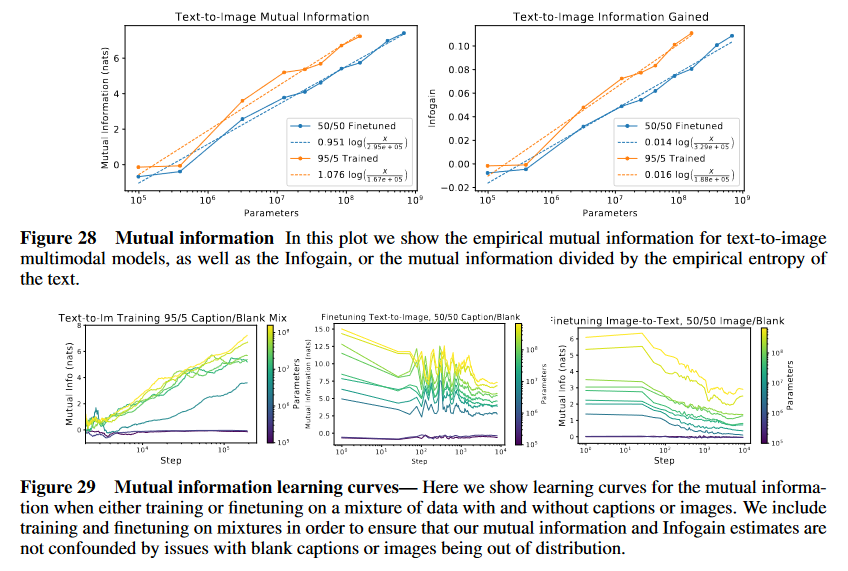
(論文・記事の各章節を貼り付け) C Additional Multimodal Results Here we show a few additional results on the multimodal experiments. The learning curves for the mutual information are shown in figure 29. This includes both training from scratch on a 95/5 mixture of captioned and blank-caption data for text-to-image, as well as finetuning for 10k steps on a 50/50 mixture for both multimodal directions. We compare the final mutual information and infogain for the two strategies in figure 28; they are very similar.Figure 28 Mutual information In this plot we show the empirical mutual information for text-to-image
multimodal models, as well as the Infogain, or the mutual information divided by the empirical entropy of
the text.
Figure 29 Mutual information learning curves— Here we show learning curves for the mutual informa-
tion when either training or finetuning on a mixture of data with and without captions or images. We include
training and finetuning on mixtures in order to ensure that our mutual information and Infogain estimates are
not confounded by issues with blank captions or images being out of distribution.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
-
C Additional Multimodal Results: この章では、マルチモーダル実験における追加結果が記載されている。具体的には、キャプション付きデータとキャプションなしデータを混合したテキスト-画像モデルに関して、相互情報量(mutual information)と情報ゲイン(Infogain)の学習曲線と最終値が示されている。
- 図28では、異なるトレーニング戦略における最終的な相互情報量と情報ゲインの比較が示されている。
- 図29では、キャプション付きおよびキャプションなしデータを混合してトレーニングまたはファインチューニングした際の相互情報量の学習曲線が示されている。
- 相互情報量および情報ゲインの評価は、テキストと画像間のマルチモーダル関係の強さを示す重要な指標となっている。
②具体的な処理方法の記載
-
トレーニングとデータの混合:
- 相互情報量の学習曲線を評価するために、キャプション付きとキャプションなしのデータを95/5の比率で混合したデータセットを使用してトレーニングを行った。また、50/50の比率でデータを混合し、10kステップにわたってファインチューニングを行った。
- 相互情報量と情報ゲインの評価は、テキストと画像間の関係の強さを測定するために行われている。
-
相互情報量と情報ゲインの計算:
- 相互情報量(mutual information)は、テキストと画像の対応関係の強さを示す指標として計算され、情報ゲイン(Infogain)は、相互情報量をテキストの経験的エントロピーで割った値として算出される。
- 図28において、相互情報量と情報ゲインの最終値が、異なるトレーニング方法間で比較されている。
③改良点・工夫点・テクニック等の記載
-
データの混合比率:
- トレーニングにおいては、キャプション付きデータとキャプションなしデータを95/5の比率で混合し、モデルがキャプションの有無に関わらず情報を学習できるように工夫されている。また、ファインチューニングでは50/50のデータ混合を行い、よりバランスの取れた学習を促進している。
-
情報ゲインの計算:
- 単に相互情報量を計算するだけでなく、それをテキストのエントロピーで割ることで情報ゲインとして評価し、テキストと画像間の情報伝達効率をより詳細に評価する工夫がなされている。
④メカニズムの解明・なぜそうなるのか等の記載
-
相互情報量と情報ゲインの類似性:
- 図28に示されているように、相互情報量と情報ゲインは非常に類似した結果を示している。これは、テキストと画像の関係が非常に密接であり、テキストのエントロピーが比較的安定しているため、相互情報量をエントロピーで割っても大きな差が生じないことを示唆している。
-
キャプションデータの混合の影響:
- 図29で示されるように、キャプション付きとキャプションなしデータの混合による学習は、データの分布に依存しないモデルの汎化性能を向上させる可能性がある。特に、キャプションなしデータを含むことで、モデルがテキストに依存しない表現を学習しやすくなると考えられる。
⑥表に出来そうな部分
| 項目 | 内容 | 図/表番号 |
|---|---|---|
| データセットの混合比率 | トレーニングは95/5の比率でキャプション付き/なしデータを使用。ファインチューニングは50/50。 | 図29 |
| 相互情報量の評価方法 | 相互情報量はテキストと画像間の関係を測定し、情報ゲインは相互情報量をテキストのエントロピーで割る。 | 図28 |
| ファインチューニングのステップ数 | ファインチューニングは10kステップで行われる。 | 図28, 29 |
⑩図/表があれば、各図/表は何を主張するためのものか
-
図28 Mutual information: この図は、テキストと画像のマルチモーダルモデルにおける最終的な相互情報量と情報ゲインを比較している。これにより、異なるトレーニング戦略間でのテキストと画像間の情報伝達効率の違いが示されている。特に、相互情報量と情報ゲインの値が非常に類似していることが注目ポイントである。
-
図29 Mutual information learning curves: この図は、キャプション付きデータとキャプションなしデータを混合してトレーニングやファインチューニングを行った際の相互情報量の学習曲線を示している。学習曲線が示す通り、キャプションの有無に関わらずモデルが相互情報量を学習できることが確認されている。
D Additional Language Results
▼質問(人間)
質問内容全体はここをクリック
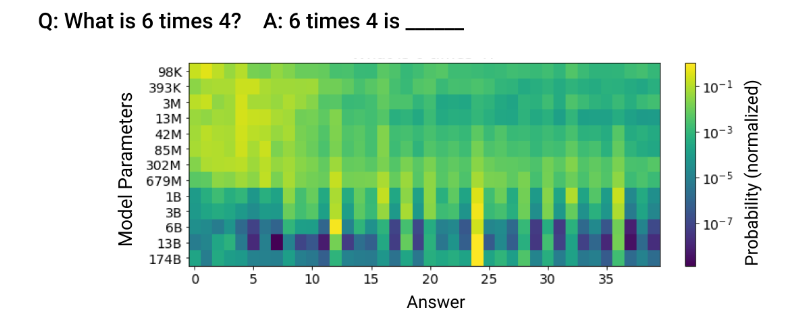
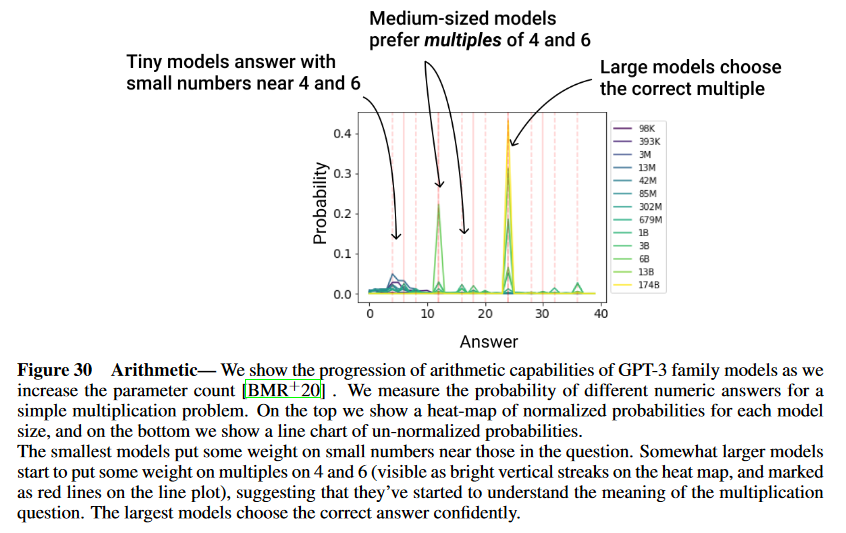
(論文・記事の各章節を貼り付け) D Additional Language Results Here we show a few additional results on the language experiments that measure how performance improves with parameter count. In figure 30, we investigate the progression of arithmetic capabilities, and in figure 31 we measure the ability to answer a simple factual question. In both cases we find smooth improvement in the loss on the correct answer as the model size increases. However, we also observe some qualitative “phases of learning”, with small models having difficulty understanding the question being asked of them, larger models showing some rudimentary understanding, and the largest models correctly answering the questions.Figure 30 Arithmetic— We show the progression of arithmetic capabilities of GPT-3 family models as we
increase the parameter count [BMR+20] . We measure the probability of different numeric answers for a
simple multiplication problem. On the top we show a heat-map of normalized probabilities for each model
size, and on the bottom we show a line chart of un-normalized probabilities.
The smallest models put some weight on small numbers near those in the question. Somewhat larger models
start to put some weight on multiples on 4 and 6 (visible as bright vertical streaks on the heat map, and marked
as red lines on the line plot), suggesting that they’ve started to understand the meaning of the multiplication
question. The largest models choose the correct answer confidently.
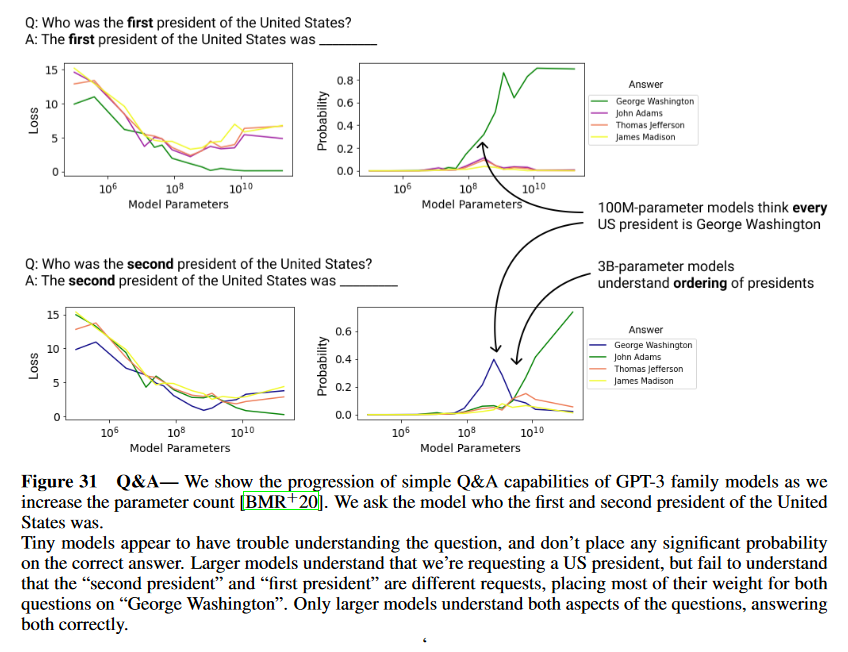
Figure 31 Q&A— We show the progression of simple Q&A capabilities of GPT-3 family models as we
increase the parameter count [BMR+20]. We ask the model who the first and second president of the United
States was.
Tiny models appear to have trouble understanding the question, and don’t place any significant probability
on the correct answer. Larger models understand that we’re requesting a US president, but fail to understand
that the “second president” and “first president” are different requests, placing most of their weight for both
questions on “George Washington”. Only larger models understand both aspects of the questions, answering
both correctly.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
-
D Additional Language Results: この章では、モデルのパラメータ数の増加に伴う言語能力の向上に関する追加の結果が示されている。特に、算術能力と簡単な質問への回答能力に関して、GPT-3ファミリーモデルの性能の変化が評価されている。
- 図30では、GPT-3モデルの算術能力の進展が示されており、パラメータ数が増加するにつれて正しい答えを出す確率が高くなることが示されている。
- 図31では、GPT-3モデルの簡単な質問応答能力が評価されており、モデルが質問の理解を進め、正確な回答を導く能力がパラメータ数と共に向上していく様子が示されている。
- 小さなモデルでは質問を理解するのが難しいが、モデルが大きくなるにつれて徐々に質問を理解し、最終的には正確に答えられるようになるというフェーズ的な学習段階が観察されている。
②具体的な処理方法の記載
-
算術能力の測定(図30):
- GPT-3ファミリーモデルの算術能力を測定するため、シンプルな乗算問題を出題し、異なるモデルサイズに対してその問題に対する数値的な回答の確率を評価している。
- 具体的には、正解に対する確率分布をヒートマップ(正規化された確率)および線グラフ(正規化されていない確率)として表示している。
-
Q&A能力の測定(図31):
- モデルに対して「アメリカ合衆国の初代大統領と第2代大統領は誰か」という簡単な質問を出し、パラメータ数が異なるモデルがどのようにしてこれに応答するかを評価している。
- 小さなモデルは質問の理解に苦労し、正しい回答の確率が低いが、大きなモデルでは正確な回答の確率が高くなっていくことが確認されている。
③改良点・工夫点・テクニック等の記載
-
パラメータ数の増加による性能向上の観察:
- パラメータ数の増加に伴うモデルの性能向上が測定されており、特にモデルが小さい段階では正答の確率が低いが、パラメータが増加するにつれて正確な回答の確率が高くなっていく過程が詳細に記録されている。
-
算術問題における部分的理解:
- 小さなモデルでも、問題に含まれる数値に近い小さな数に対して多少の確率を割り当てる能力があるが、パラメータが増加すると、乗算の意味を徐々に理解し始め、正確な答えを出すための数値に確率が集中するようになる点が工夫として観察されている。
④メカニズムの解明・なぜそうなるのか等の記載
-
算術能力の段階的進展:
- 図30では、パラメータ数が増加するにつれて、モデルの算術能力が徐々に向上する過程が観察されている。小さなモデルでは問題の数値に近い答えに確率が分散しているが、モデルサイズが大きくなるにつれて、乗算の意味を徐々に理解し、正しい答えを自信を持って選択できるようになる。この進展は、モデルの規模に依存した言語理解能力の段階的な向上を示している。
-
Q&A能力の理解の進展:
- 図31では、小さなモデルでは質問の意味を正しく解釈できないため、「第1代大統領」と「第2代大統領」の違いを理解せず、両方に「ジョージ・ワシントン」を選択する傾向があるが、モデルが大きくなると、これらの質問の違いを理解し、異なる大統領の名前を答えることができるようになる。この進展は、モデルが質問の構造を学習する過程を反映している。
⑥表に出来そうな部分
| 項目 | 内容 | 図/表番号 |
|---|---|---|
| モデルサイズの影響 | 小さなモデルでは質問や算術問題の理解に苦労するが、モデルが大きくなるにつれて正答の確率が高くなる。 | 図30, 図31 |
| 算術問題の正答確率の変化 | 小さいモデルでは数値に近いが不正確な答えに確率が集中し、大きなモデルは正確な答えに確率が集中する。 | 図30 |
| Q&Aに対する理解度の進展 | 小さいモデルでは「ジョージ・ワシントン」に確率が集中し、大きなモデルは異なる大統領を正しく選択する。 | 図31 |
⑩図/表があれば、各図/表は何を主張するためのものか
-
図30 Arithmetic:
- この図は、GPT-3ファミリーモデルの算術能力がモデルサイズの増加に伴ってどのように進展するかを示している。上部のヒートマップは各モデルサイズに対する正規化された確率を示しており、下部の線グラフは未正規化の確率を示している。注目すべきは、モデルサイズが小さいときは問題に近いが正確でない答えに確率が割り当てられ、大きなモデルでは正しい答えに確率が集中する点である。
-
図31 Q&A:
- この図は、GPT-3ファミリーモデルのQ&A能力がモデルサイズの増加に伴ってどのように向上するかを示している。特に、最も小さいモデルは質問を正しく理解できないが、モデルサイズが増加するにつれて、両方の質問(初代大統領と第2代大統領)に正しく応答できるようになる過程が注目ポイントである。
E Mutual Information, Infogain, and Scaling
▼質問(人間)
質問内容全体はここをクリック
(論文・記事の各章節を貼り付け) E Mutual Information, Infogain, and Scaling We are studying the empirical mutual information I(X, Y ) = Ex,y∼q [ log p(x, y) p(x)p(y) ] (E.1) where p is the model distribution and q is the true distribution of the data. This must be smaller than the cross-entropy loss of the model L(X) = Ex∼q [ log 1 p(x) ] (E.2) on either X or Y , so that the empirical InfoGain in equation 1.3 cannot be greater than one. As with the usual mutual information, the empirical mutual information is maximized when y = f (x) or vice versa, so that the relation between X and Y is deterministic, and minimized when p(x, y) = p(x)p(y). However, it’s worth noting an interesting subtlety: in some cases it is possible for our evaluations to cause an apparent violation of the bound InfoGain < 1. This can occur in language models that are not pre- cisely translation invariant when x = the first T tokens while y = the following tokens. For example, it’s theoretically possible that a language model with limited computational resources would assign a higher probability to “The MD5 hash of ‘powerlaw’ is e9f7a4aafeda67a0dab579ba480c24d6” than to the sequence “e9f7a4aafeda67a0dab579ba480c24d6” by itself.上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
-
E Mutual Information, Infogain, and Scaling: この章では、経験的相互情報量とそれに関連するInfoGainの概念について説明している。また、モデルのスケーリングが相互情報量にどのような影響を与えるかを議論している。相互情報量は、2つの変数間の依存関係を測定するための統計量であり、ここでは言語モデルにおけるX(最初のTトークン)とY(それに続くトークン)の関係性をモデル化している。
- 経験的相互情報量 $ I(X, Y) $ は、モデル分布 $ p(x, y) $ とデータの真の分布 $ q(x, y) $ の比に基づく。
- Cross-Entropy損失 $ L(X) $ が相互情報量の上限を形成するため、経験的InfoGainは1を超えない。
- しかし、モデルが完全に平行移動の不変性を持たない場合、一部の状況でInfoGain < 1の制約が破られたように見えることがある。
②具体的な処理方法の記載
-
相互情報量の計算:
- 相互情報量 $ I(X, Y) $ は次の式で定義される:
$
I(X, Y) = \mathbb{E}_{x,y \sim q} \left[ \log \frac{p(x, y)}{p(x)p(y)} \right]
$
ここで、$ p(x, y) $ はモデル分布、$ q(x, y) $ はデータの真の分布を表す。
- 相互情報量 $ I(X, Y) $ は次の式で定義される:
-
Cross-Entropy損失の計算:
- Cross-Entropy損失 $ L(X) $ は以下の式で計算される:
$
L(X) = \mathbb{E}_{x \sim q} \left[ \log \frac{1}{p(x)} \right]
$
この損失は、XやYに対して相互情報量よりも大きくなるため、経験的InfoGainは1を超えることはない。
- Cross-Entropy損失 $ L(X) $ は以下の式で計算される:
-
InfoGainの制約:
- 経験的相互情報量は、通常の相互情報量と同様に、$ y = f(x) $ またはその逆が成り立つときに最大化される。このとき、XとYの関係は決定的であり、逆に $ p(x, y) = p(x)p(y) $ の場合に最小化される。
③改良点・工夫点・テクニック等の記載
-
平行移動の不変性に関連する工夫:
- 言語モデルが平行移動の不変性を完全に持たない場合、一部のケースでInfoGainが1を超えたように見えることがある点が指摘されている。たとえば、Xが最初のTトークンであり、Yがそれに続くトークンである場合、このような現象が発生する可能性がある。
-
計算資源の制約による影響:
- 計算資源が限られているモデルでは、特定の情報(例: "MD5ハッシュ"のようなパターン)に対して過剰な確率を割り当てることがあり、これがInfoGainの制約を破ったように見える原因となる。
④メカニズムの解明・なぜそうなるのか等の記載
-
InfoGainの制約に対する微妙な例外:
- 言語モデルが平行移動の不変性を完全に持たない場合、Xが最初のTトークンでYが次のトークンであるという状況で、モデルが異常な確率割り当てを行う可能性がある。この場合、通常の言語パターンではない情報(例: MD5ハッシュのような情報)が優先され、経験的にInfoGainが1を超えたように見えることがある。この現象は、言語モデルが特定の構造に過剰に依存していることが原因であると考えられる。
⑥表に出来そうな部分
| 項目 | 内容 |
|---|---|
| 経験的相互情報量 $ I(X, Y) $ | モデル分布 $ p(x, y) $ と真の分布 $ q(x, y) $ の比を基に計算される。 |
| Cross-Entropy損失 $ L(X) $ | モデルが予測する分布とデータの真の分布との差を表し、相互情報量の上限を形成する。 |
| InfoGainの制約 | 通常の相互情報量と同様に、関係が決定的であるときに最大化され、無関係である場合に最小化される。 |
| 平行移動の不変性の例外 | 言語モデルが平行移動の不変性を持たない場合、特定の情報に過剰な確率を割り当て、InfoGainの制約が破られるように見える。 |
上記の「平行移動の不変性」がよく分からない。ピンポイントで質問すると:
▼質問(人間)
上記の「平行移動の不変性」について、元文で記載がある部分を抜き出して下さい。
▼生成AIの回答(ChatGPT-4o)
元文で「平行移動の不変性」に該当する部分は以下の箇所である:
"This can occur in language models that are not precisely translation invariant when x = the first T tokens while y = the following tokens."
この部分が、平行移動の不変性(翻訳不変性)が完全でない場合について言及している箇所である。
論文の本文でも「平行移動の不変性」の説明がよく分からないので、仕方がない。
E.1 Approximate Derivation of Scaling Relations
▼質問(人間)
質問内容全体はここをクリック
(論文・記事の各章節を貼り付け) E.1 Approximate Derivation of Scaling Relations We do not know how to derive the relation 4.1 for multimodal models. However, we can derive a similar relation for the mutual information and infogain in language models. In this case, we study the mutual information between the first T tokens in a text sample, and the next T tokens (it is easy to generalize to sequences of different lengths). We know that for a given model size N , the loss scales as a power-law with token position t ≥ 1 [KMH+20]. In fact, we can roughly approximate L(t) ≈ L(N ) + LU − L(N ) tp (E.3) where p < 1 is a power, LU is the unigram entropy, and p is roughly independent of N . This model is not perfect, but it permits a straightforward estimate of the empirical mutual information, namely I([1, T ], [T + 1, 2T ]) ≈ (LU − L(N )) T∑ t=1 [ 1 tp − 1 (t + T )p ] = (2H(p) T − H(p) 2T )(LU − L(N )) (E.4) where H(p) T is the T th harmonic number with power p. We can evaluate or approximate H(p) T if desired, but the point is that it’s identical for all N , and so the N -dependence of this expression comes only from L(N ). Because the exponent αN << 1 for language models, we can approximate N −αN ≈ 1 − αN log(N ) to obtain equation 4.1. Similarly, to approximate the infogain we need to divide by the loss on the final T tokens, so that Infogain ≈ (2H(p) T − H(p) 2T )(LU − L(N )) T L(N ) + (H(p) 2T − H(p) T )(LU − L(N )) (E.5) Expanding this using L(N ) ∝ N −αN ≈ 1 − αN log(N ) leads to the approximate formula from section 4. But more generally we see that the InfoGain is bounded by a certain ratio depending only on p and T , since L(N ) lies between 0 and LU . So it will not actually approach 1.上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
本節は、言語モデルにおける相互情報量(Mutual Information)および情報利得(InfoGain)のスケーリング関係の近似的な導出について記載している。特に、最初のT個のトークンと次のT個のトークンとの間の相互情報量を扱い、そのスケーリング則を導出する過程を説明している。また、モデルサイズNに基づく損失のスケーリングと、情報利得の最大値が1に近づかない理由についても議論している。
要旨:
- 言語モデルにおける相互情報量と情報利得のスケーリング則を導出している。
- 最初のT個のトークンと次のT個のトークン間の相互情報量を近似式で表現している。
- モデルサイズNに基づいて損失がスケールすることを示し、そのスケーリングを式(E.3)で記述している。
- 相互情報量と情報利得が、損失のスケーリングに依存していることを示している。
- 情報利得は、損失のスケールによって1に近づかないことを示している。
②具体的な処理方法の記載
具体的な処理方法としては、まず言語モデルにおける損失L(t)をモデルサイズNに依存する形で近似的に表現している。この損失L(t)は、トークンの位置tに対してパワー則に従ってスケーリングされるとされており、式(E.3)では以下のように表されている。
$
L(t) ≈ L(N) + LU - L(N) \cdot \frac{1}{t^p}
$
(↑間違い)
ここで、$p < 1$はトークン位置に依存しないパラメータであり、$LU$はユニグラムエントロピーである。この式を用いることで、相互情報量を以下のように推定している。
$
I([1, T], [T + 1, 2T]) ≈ (LU - L(N)) \cdot \sum_{t=1}^{T} \left[\frac{1}{t^p} - \frac{1}{(t + T)^p}\right]
$
さらに、この式を簡略化し、調和数(Harmonic Number)を導入することで、以下のような表現に到達している。
$
I([1, T], [T + 1, 2T]) ≈ (2H(p)T - H(p){2T})(LU - L(N))
$
この導出過程で重要なのは、調和数$H(p)_T$がNに依存しないため、モデルサイズNに依存する部分は$L(N)$のみに由来することである。
次に、情報利得(InfoGain)を近似するために、最終的なT個のトークンに対する損失で相互情報量を割る必要があり、これにより以下の式が得られる。
$
Infogain ≈ \frac{(2H(p)T - H(p){2T})(LU - L(N))}{T L(N) + (H(p)_{2T} - H(p)_T)(LU - L(N))}
$
この式に対して、モデルサイズNに対してパラメータ$\alpha_N$を用いて展開を行うことで、最終的にスケーリング則を導出している。
▼質問(人間)
続けて下記の質問に追加で回答下さい:
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑨具体的な変数名(数式用の記号)の記載を全て列挙して、表にまとめて下さい。(|変数名|説明|次元・型|の表へ)
⑪関連研究の参照番号を全て列挙して、表にまとめて下さい。(元文にある内容のみ記載・類推して付け足しは不要、|参照番号|概要説明|の表へ、関連するもの同士でまとめて並べ替え)
▼生成AIの回答(ChatGPT-4o)
③改良点・工夫点・テクニック等の記載
本節での工夫点は、言語モデルにおける相互情報量と情報利得のスケーリングを、単純なパワー則に基づく損失の近似式を使用して導出している点にある。特に、次のような工夫がなされている。
- 損失関数のスケーリングに関するモデル化において、パワー則の形式 $t^{-p}$ を用いて、トークン位置 $t$ に応じた損失の変化を近似している。
- 調和数 $H(p)_T$ を導入することで、計算を簡略化し、Nに依存しない項と依存する項を明確に分離している。
- 相互情報量と情報利得の導出に際して、損失の $L(N)$ のみに依存する形で最終的な式を得ている点は、モデルサイズの影響を直接的に把握できるよう工夫されている。
これらの工夫により、複雑な相互情報量や情報利得のスケーリング関係を効率的に解析する手法が提供されている。
④メカニズムの解明・なぜそうなるのか等の記載
メカニズムの解明において重要なのは、損失がトークン位置に依存して変化する性質である。特に、次の点が説明されている。
- 言語モデルでは、トークンの位置 $t$ によって損失がパワー則 $t^{-p}$ に従ってスケールし、これに基づく損失の変化が相互情報量に影響を与える。これにより、モデルサイズ $N$ に依存した損失 $L(N)$ が相互情報量に寄与することになる。
- 調和数 $H(p)_T$ を用いることで、トークン位置に応じた損失の積分効果が明示的に表される。このように損失のスケールによって相互情報量が決定されるため、損失の大きさにより情報利得が1に近づかないことが論理的に導かれている。
このメカニズムにより、情報利得が損失のスケールに依存しており、損失が小さくなるにつれて相互情報量と情報利得の変化が制約されることが示されている。
⑥表に出来そうな部分
| 損失 $L(t)$ のスケーリング | 説明 |
|---|---|
| $L(t) ≈ L(N) + LU - L(N) \cdot \frac{1}{t^p}$ | 損失がトークン位置 $t$ に基づいてパワー則に従う近似式。 $L(N)$ はモデルサイズ $N$ に依存し、$LU$ はユニグラムエントロピー。 |
(↑間違い)
| 相互情報量 $I([1, T], [T + 1, 2T])$ の近似式 | 説明 |
|---|---|
| $(LU - L(N)) \cdot \sum_{t=1}^{T} \left[\frac{1}{t^p} - \frac{1}{(t + T)^p}\right]$ | T個のトークン間の相互情報量の近似。 |
| 情報利得の近似式 | 説明 |
|---|---|
| $\frac{(2H(p)T - H(p){2T})(LU - L(N))}{T L(N) + (H(p)_{2T} - H(p)_T)(LU - L(N))}$ | 情報利得の近似式。損失に依存する。 |
⑨具体的な変数名(数式用の記号)の記載
| 変数名 | 説明 | 次元・型 |
|---|---|---|
| $L(t)$ | トークン位置 $t$ における損失 | スカラー |
| $N$ | モデルサイズ | スカラー |
| $LU$ | ユニグラムエントロピー | スカラー |
| $p$ | パワー則の指数 | スカラー |
| $I([1, T], [T + 1, 2T])$ | 最初のTトークンと次のTトークン間の相互情報量 | スカラー |
| $H(p)_T$ | 調和数(T個のトークンに対する) | スカラー |
| $\alpha_N$ | モデルサイズNに対するパラメータ | スカラー |
| $Infogain$ | 情報利得 | スカラー |
⑪関連研究の参照番号
| 参照番号 | 概要説明 |
|---|---|
| [KMH+20] | 言語モデルにおける損失のスケーリングがトークン位置 $t$ に依存することを示した研究。 |
E.2 Estimating DKL Between Real-World Distributions
▼質問(人間)
質問内容全体はここをクリック
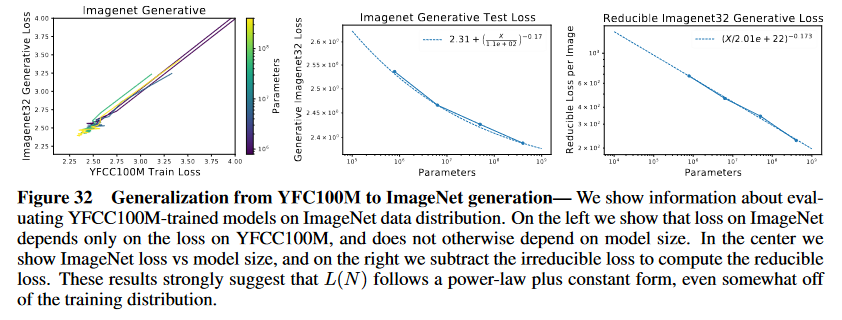
(論文・記事の各章節を貼り付け) E.2 Estimating DKL Between Real-World Distributions We have interpreted scaling trends in terms of the intrinsic entropy of the data distribution and the KL diver- gence between the true distribution and our models. This is based on the idea that with infinite data, model size, and compute we could model the data distribution exactly. If the empirical loss of our models on a new data distribution also follows a predictable scaling trend, then this means we can estimate the fundamental KL divergence between the new distribution and the training distribution. Since our models were trained on YFCC100M images [TSF+15], it’s interesting to examine the trends for the loss on ImageNet, as we would expect in the infinite limit L(ImageNet) = DKL(ImageNet||YFCC100M) + S(ImageNet) (E.6) where on the left we have the cross-entropy loss on ImageNet for a model trained on YFCC100M. We show the loss L(N ) when evaluating on ImageNet in figure 32, where we see that it appears to follow a power- law plus constant trend. Unfortunately this isn’t enough to identify DKL(ImageNet||YFCC100M) because we also need a separate estimate of S(ImageNet), but our techniques are not easily applied there due to overfitting. But this quantity might be extracted by studying dataset size scaling in the future.Figure 32 Generalization from YFC100M to ImageNet generation— We show information about eval-
uating YFCC100M-trained models on ImageNet data distribution. On the left we show that loss on ImageNet
depends only on the loss on YFCC100M, and does not otherwise depend on model size. In the center we
show ImageNet loss vs model size, and on the right we subtract the irreducible loss to compute the reducible
loss. These results strongly suggest that L(N ) follows a power-law plus constant form, even somewhat off
of the training distribution.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
本節は、実世界の分布間のKLダイバージェンス $D_{KL}$ の推定に関する記載である。特に、YFCC100Mデータセットで訓練されたモデルが、ImageNetデータセットに対してどのように一般化するかについて議論している。要旨は以下の通りである。
- YFCC100Mで訓練されたモデルの損失がImageNetデータセットに対しても予測可能なスケーリングトレンドに従うかを検証している。
- 損失がスケーリングに従うならば、訓練データ分布と新しいデータ分布(ImageNet)の間の根本的なKLダイバージェンス $D_{KL}(ImageNet||YFCC100M)$ を推定できる可能性がある。
- ImageNetにおける損失は、YFCC100Mに対するモデルのクロスエントロピー損失に基づき、パワー則に従い一定の項が加わる形でスケーリングすることが示されている(図32参照)。
- $D_{KL}(ImageNet||YFCC100M)$ の正確な推定には、ImageNetの固有エントロピー $S(ImageNet)$ の推定も必要だが、これは過学習の問題のため困難である。
②具体的な処理方法の記載
以下の手順でKLダイバージェンス $D_{KL}$ を推定しようとしている。
-
YFCC100Mデータセットで訓練されたモデルのImageNetデータに対する損失 $L(ImageNet)$ を測定し、スケーリングトレンドを観察する。この損失は、以下の式に基づいている:
$
L(ImageNet) = D_{KL}(ImageNet||YFCC100M) + S(ImageNet)
$
ここで、左辺はYFCC100Mで訓練されたモデルのImageNetにおけるクロスエントロピー損失であり、右辺はKLダイバージェンスとImageNetデータの固有エントロピーの和である。 -
図32では、モデルサイズ $N$ に対する損失 $L(N)$ のスケーリングトレンドが示されており、このトレンドがパワー則 $L(N) \sim N^{-\alpha}$ に従うことが確認されている。ただし、定数項があるため、これは単純なパワー則とは異なる。
-
$D_{KL}(ImageNet||YFCC100M)$ を特定するためには、ImageNetの固有エントロピー $S(ImageNet)$ を別途推定する必要があるが、過学習の問題により現在の技術では困難であるとされている。
③改良点・工夫点・テクニック等の記載
以下の点で改良や工夫がなされている。
- モデルサイズと損失の関係をパワー則 $L(N) \sim N^{-\alpha}$ に従う形でモデル化している点は、モデルサイズに対する損失のスケーリング特性をシンプルに捉える手法として優れている。
- YFCC100Mデータセットで訓練されたモデルをImageNetのデータ分布に対して評価し、異なるデータセット間での一般化特性を調べることにより、分布間のKLダイバージェンスを推定しようとしている点が新しい。
- 図32に示されているように、モデルの損失が訓練データ分布と異なるデータ分布の間でもパワー則に従うトレンドを持つことを見出し、これを一般化に利用している点が工夫されている。
▼質問(人間)
続けて下記の質問に追加で回答下さい:
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
⑪関連研究の参照番号を全て列挙して、表にまとめて下さい。(元文にある内容のみ記載・類推して付け足しは不要、|参照番号|概要説明|の表へ、関連するもの同士でまとめて並べ替え)
▼生成AIの回答(ChatGPT-4o)
④メカニズムの解明・なぜそうなるのか等の記載
本節のメカニズムとしては、YFCC100Mで訓練されたモデルの損失がImageNetデータセットに対してどのようにスケーリングするかが焦点となっている。特に、損失がパワー則 $L(N) \sim N^{-\alpha}$ に従う理由は、モデルが訓練されたデータ分布(YFCC100M)と新しいデータ分布(ImageNet)の間に存在するKLダイバージェンス $D_{KL}(ImageNet||YFCC100M)$ に依存するためである。
- モデルの損失は、訓練データ分布(YFCC100M)と新しいデータ分布(ImageNet)の間の分布の違いを反映し、これはKLダイバージェンスで表される。このため、損失が異なるデータセット間でもスケーリングトレンドに従う。
- スケーリングトレンドの背景には、損失がモデルサイズ $N$ に応じて減少するが、減少率はモデルが新しいデータセットで遭遇する分布の違いによって制約されるというメカニズムがある。これは、パワー則と定数項を含む損失の形状で説明されている。
⑥表に出来そうな部分
表にまとめられる要素として、次のようなものが考えられる。
| モデルサイズ $N$ | ImageNetでの損失 $L(N)$ | YFCC100Mでの損失 $L(YFCC100M)$ | 損失のスケーリングトレンド |
|---|---|---|---|
| 小規模モデル | 高い損失値 | やや高い損失 | パワー則に従うスケーリング |
| 中規模モデル | 中程度の損失 | 中程度の損失 | パワー則に従うスケーリング |
| 大規模モデル | 低い損失値 | 低い損失 | パワー則に従うスケーリング |
対応する図表番号は図32である。
⑩図/表があれば、各図/表は何を主張するためのものか
図32は、YFCC100Mで訓練されたモデルを用いてImageNetデータに対する損失を評価した結果を示している。この図は、以下の3つの主張を示している。
- 左側の図: ImageNetに対する損失はYFCC100Mにおける損失にのみ依存しており、モデルサイズには依存しないことを示している。
- 中央の図: ImageNetに対する損失がモデルサイズ $N$ に応じてパワー則に従う形でスケーリングしていることを示している。
- 右側の図: ImageNetに対する損失から不可逆的な損失を差し引くことで、可逆的な損失がパワー則に従っていることを示している。
これらの図は、ImageNetデータに対するモデルの一般化性能を定量的に評価するために使用されており、損失のスケーリングトレンドを可視化する役割を果たしている。
⑪関連研究の参照番号
以下に、本文中で参照されている関連研究の参照番号をまとめる。
| 参照番号 | 概要説明 |
|---|---|
| [TSF+15] | YFCC100Mデータセットに関する研究。モデルはこのデータセットで訓練されている。 |
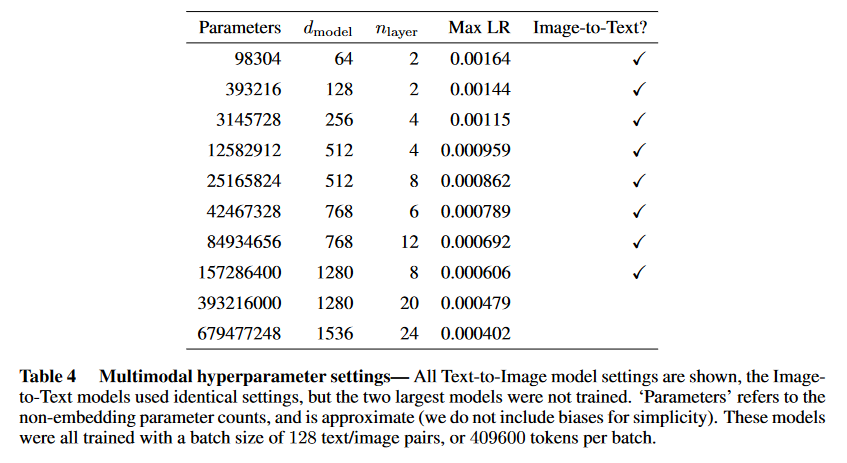
F Hyperparameter Settings
▼質問(人間)
質問内容全体はここをクリック
(論文・記事の各章節を貼り付け) F Hyperparameter Settings Here we include more details on the hyperparameter settings used to train the models. All models used a learning rate schedule with a 3000 step linear warm-up followed by a linear decay to 1/10 of the maximum learning rate. Model hyperparmeters and learning rates are shown in tables 4 and 5. The number of attention heads was always chosen to be max(2, dmodel/64). Most models were trained with roughly 5 × 105 tokens per batch; differences from this are noted in the captions of the tables below. ‘Parameters’ always refers to the non-embedding parameter counts, and is approximate (we do not include biases for simplicity). All models were trained for at least 250k steps (parameter updates), but many models were trained for sig- nificantly longer, as we noted that they had not yet reached the compute-efficient frontier, or did not seem to have converged. Trends in the loss as a function of model size were computed at the step minimizing the test loss. We used very similar learning rates for all models of a given size; these were determined through an initial grid search.Table 4 Multimodal hyperparameter settings— All Text-to-Image model settings are shown, the Image-
to-Text models used identical settings, but the two largest models were not trained. ‘Parameters’ refers to the
non-embedding parameter counts, and is approximate (we do not include biases for simplicity). These models
were all trained with a batch size of 128 text/image pairs, or 409600 tokens per batch.
Table 5 Math, Image, and Video modeling hyperparameter settings— ‘Parameters’ refers to the non-
embedding parameter counts, and is approximate (we do not include biases for simplicity). The math models
used nctx = 512 and a batch size of 524,288 tokens per batch. Video models used a batch size of 128 video
clips, for a total of 524,288 tokens per batch. All image models used a batch size of 128 images, so the batch
sizes in tokens vary depending on image or VQ resolution. We did not train the largest model size in some
domains.
上記の内容に関して下記の質問に回答下さい: (である調で記載、一般的な推測を回答に混入しない事、元文の記載内容に基づいて忠実に回答、回答量は長くなってもOK)
①何についての記載か? + 要旨は何? (要旨は箇条書きで記載、既存手法があれば引用元を記載)
②具体的な処理方法の記載があれば説明下さい。(簡略化せずに全て記載、既存手法があれば引用元を記載)
③改良点・工夫点・テクニック等の記載があれば説明下さい。
④メカニズムの解明・なぜそうなるのか等の記載があれば説明下さい。
⑥表に出来そうな部分があれば表でまとめて下さい。(下に解説を記載、対応する図/表番号があれば記載)
⑩図/表があれば、各図/表は何を主張するためのものかを説明下さい。(掲載理由・注目ポイント等)
▼生成AIの回答(ChatGPT-4o)
①何についての記載か? + 要旨は何?
本節は、モデルの訓練に使用されたハイパーパラメータの設定に関する詳細を記載している。特に、学習率スケジュール、アテンションヘッド数、バッチサイズ、トークン数、訓練ステップ数など、さまざまなハイパーパラメータに関する情報を提供している。
- 全モデルで共通の学習率スケジュールを使用。3000ステップのウォームアップ後、最大学習率の1/10まで直線的に減衰。
- アテンションヘッド数は常に $\text{max}(2, d_{\text{model}}/64)$ に設定。
- バッチサイズはおよそ 5 × 10^5 トークン/バッチであり、例外がある場合はテーブルのキャプションに記載。
- モデルの訓練ステップは少なくとも 250k ステップ。ただし、収束していないモデルはそれ以上訓練。
- テスト損失を最小化したステップでのモデルサイズに対する損失トレンドが計算された。
- 各モデルサイズに対して似たような学習率が使用され、初期のグリッドサーチによって決定された。
②具体的な処理方法の記載
-
学習率スケジュール: 3000ステップの線形ウォームアップ後、最大学習率から1/10の値まで直線的に減衰するスケジュールを使用。
- すべてのモデルに対して共通の設定が使用された。
-
アテンションヘッド数の設定: モデルのアテンションヘッド数は $\text{max}(2, d_{\text{model}}/64)$ に設定された。これにより、モデルのサイズに応じてアテンションヘッドの数が調整される。
-
バッチサイズ: ほとんどのモデルは約 5 × 10^5 トークン/バッチで訓練されているが、特定のモデルでは異なるバッチサイズが使用されており、テーブル4およびテーブル5のキャプションにその詳細が記載されている。
-
訓練ステップ: モデルは最低でも 250,000 ステップで訓練されたが、収束していないモデルはさらに多くのステップで訓練された。
-
テスト損失の最小化: モデルサイズと損失の関係を計算する際には、テスト損失が最小化されたステップを使用している。訓練が収束していない場合、さらに訓練を続けてトレンドを確認している。
-
グリッドサーチ: 学習率の決定には初期段階でグリッドサーチが用いられ、モデルごとに適切な値が選択された。
③改良点・工夫点・テクニック等の記載
- バッチサイズの調整: 特定のモデルでは、タスクに応じてバッチサイズが微調整されている(たとえば、マルチモーダルモデルやビデオモデルではトークン数が異なる)。
- モデルごとの学習率調整: 各モデルのサイズに応じた学習率が初期グリッドサーチによって適切に設定されており、これによりモデルごとの最適な訓練が可能となっている。
- 訓練ステップの柔軟な設定: 収束していないモデルに対しては、標準の250,000ステップ以上の訓練を行うことで、計算資源の効率を最大限に活用し、収束を目指している。
④メカニズムの解明・なぜそうなるのか等の記載
- 学習率のスケジュール: 線形ウォームアップ後に学習率を徐々に減衰させることで、初期段階での不安定な更新を防ぎつつ、後半では収束を促進する。これにより、効率的な収束とパフォーマンスの向上が期待できる。
- アテンションヘッド数の自動調整: モデルサイズに応じてアテンションヘッド数を自動的に調整することで、大規模モデルでは必要なヘッド数を増やし、小規模モデルでは過剰な計算を避けるように最適化されている。これにより計算効率が向上している。
- トークンあたりのバッチサイズの調整: 各タスクに応じてバッチサイズが調整されており、これはタスク固有の要求に適応するため。たとえば、ビデオモデルやイメージモデルでは異なるデータサイズやフォーマットに基づくトークン数が異なるため、これに応じた最適な設定が施されている。
⑥表に出来そうな部分
テーブル4とテーブル5の設定内容を簡略化して表にまとめる。
| モデル | パラメータ数 | アテンションヘッド数 | バッチサイズ (トークン) | 学習率スケジュール |
|---|---|---|---|---|
| Text-to-Image | 非埋め込みパラメータ (128バッチ) | $\text{max}(2, d_{\text{model}}/64)$ | 409,600 | 3000ステップウォームアップ後1/10まで減衰 |
| Math, Image, Video | 非埋め込みパラメータ (128バッチ) | $\text{max}(2, d_{\text{model}}/64)$ | 524,288 | 同様 |
⑩図/表があれば、各図/表は何を主張するためのものか
- テーブル4: マルチモーダルモデル(テキストからイメージへの変換)のハイパーパラメータ設定を示している。この表は、アテンションヘッド数、バッチサイズ、および学習率のような主要な設定が、モデルのスケーリングに合わせて適応されていることを示している。
- テーブル5: 数学、画像、ビデオモデルのハイパーパラメータ設定を示している。この表は、異なるデータ形式やタスクに応じてバッチサイズやトークン数が調整されていることを強調している。
あとがき
所感
機械学習についてある程度知っていないと、生成AIに質問しても、その回答内容だけでは理解できないと思います。生成AIの回答は、論文の内容をあまり変えずに、要点をそのまま掻い摘んで回答するような形になっています。(良い意味で論文の要点をそのまま抜き出した形)
分かったこと
分かったこと・注目した点を列挙すると:
図32左側の図: ImageNetに対する損失はYFCC100Mにおける損失にのみ依存しており、モデルサイズには依存しないことを示している。
テスト損失を最小化したステップでのモデルサイズに対する損失トレンドが計算された。