はじめに
東京工業大学/株式会社Nospare の栗栖です.
この記事では関数時系列データに対する主成分分析 (principal component analysis, PCA) について紹介します.関数データに対するPCA (functional PCA, FPCA) を利用した統計分析は数多く知られていますが,今回は特に関数時系列データの2標本検定と予測に焦点を当てて紹介します.また関数データ解析についてについて馴染みがない方・より詳しく知りたい方向けに,Rを利用した簡単な関数データ解析の例と関数データ分析について解説されたテキストについて有名なものをいくつか紹介します.
関数データの例
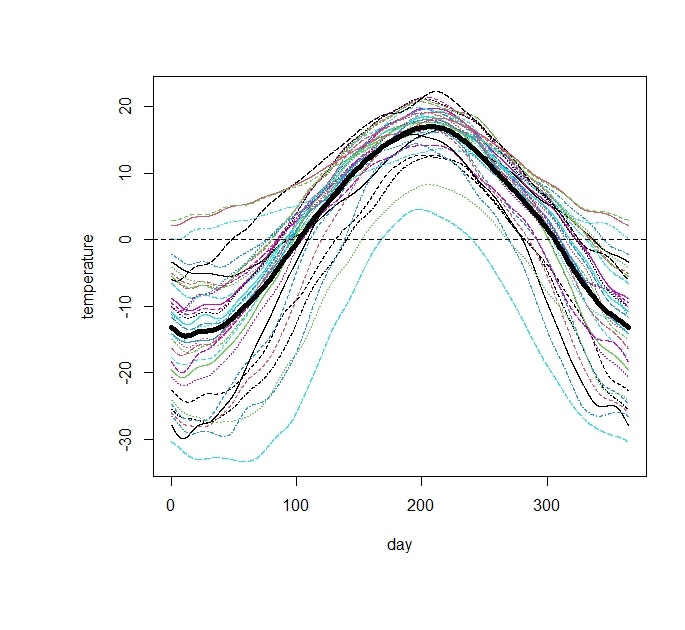
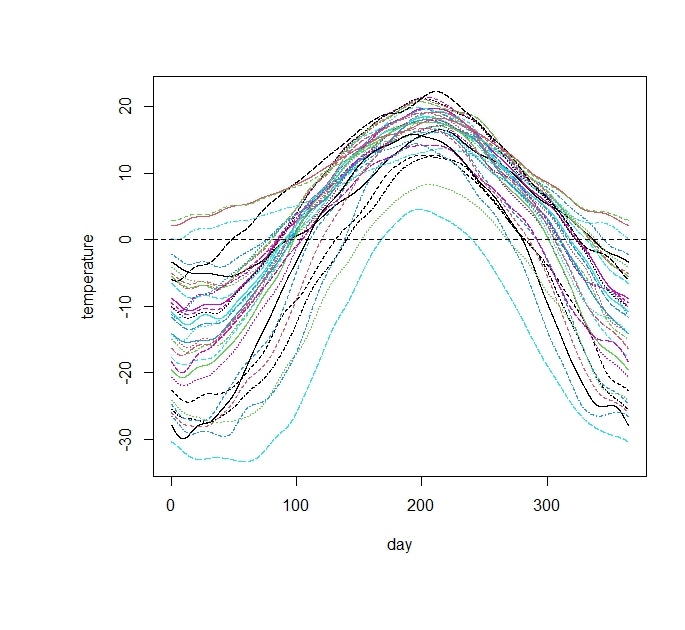
以下の図は R のパッケージ fdaに含まれるカナダの35都市における一年間の気温のデータです.縦軸が気温,横軸が日(1~365)に対応しています.図の中の各曲線が各都市の年間の気温に対応しています.気温のデータ以外にも,各都市における PM10 の観測値(Aue et al.(2015)) や一日の中での株価の変化(Li et al.(2020))など,様々な分野での応用例が知られています.このように通常の多変量解析や時系列解析と異なり,(各地点・時点で得られる)データが数値ではなく関数(曲線)として得られるものを関数データといい,関数データを扱う統計学の分野は関数データ解析と呼ばれます.
関数主成分分析(FPCA)
FPCAは多変量解析で用いられる主成分分析(PCA)を関数データの枠組みに拡張したもので,PCAで成り立つ結果の多くはFPCAでも成り立ちます.多変量解析のメインツールは線形代数(有限次元)ですが,関数データ解析でのメインツールは関数解析(大雑把に言うと無限次元の線形代数)に代わります.
$X = \{X_{t}\}_{t \in \mathbb{Z}}$ を関数(時系列)データ, $X_1,\dots,X_T$ が観測値として得られているとします.ここで,各 $X_{t}$ は内積 $\langle \cdot, \cdot \rangle$をもつヒルベルト空間 $H$ に値をとるとしておきます.特に$H = \mathbb{R}^{d}$ の時は通常の多変量(時系列)解析に対応します.共分散オペレーター $C: H \to H$ は$C=E[X_t \otimes X_t]=E[\langle X_t, \cdot \rangle X_t]$ で定義され,以下のように特異値分解できることがわかります:
C(x) = \sum_{j=1}^{\infty}\lambda_j \langle v_j, x \rangle v_j,\ x \in H.
ここで $\{\lambda_j\}$, $\{v_j\}$ はそれぞれ $C$ の固有値(eigenvalue),固有関数(eigenfunction)と呼ばれ,特に $\lambda_1 \geq \lambda_2 \geq \dots$,
C(v_{j})=\lambda_j v_j,\quad \|v_j\|= \sqrt{\langle v_j, v_j \rangle} =1,\quad \langle v_j, v_k \rangle=0\ (j \neq k)
を満たします.上記の分解は線形代数における行列の固有値分解に対応しています.$\{v_j\}$ は主成分分析における固有ベクトルに対応します.また $\{v_j\}$ は空間 $H$ の正規直行基底を構成するので,これらを用いて$X_t$を以下のように展開することができます(Karhunen-Loeve 展開):
X_{t} = \sum_{j=1}^{\infty}\langle X_{t},v_{j} \rangle v_{j}.
上記の展開において $\langle X_t, v_j \rangle$ は $X_t$ の関数主成分スコア(FPCA score) と呼ばれます.共分散オペレータ $C$ は
\hat{C} = {1 \over T}\sum_{t=1}^{T} (X_t-\bar{X}_{T}) \otimes (X_t - \bar{X}_{T})
で推定することができます.ただし,$\bar{X}_{T}={1 \over T}\sum_{t=1}^{T}X_{t}$ はデータの平均です.実際,適当な条件のもとで一致性をもつことが示せます:
E[\|\hat{C}-C\|_{\mathcal{S}}^{2}] = O\left({1 \over T}\right).
($\|\cdot\|_{\mathcal{S}}$ はヒルベルトーシュミットノルム, $\hat{C}$ と $C$ の近さを測る指標)
共分散オペレーター $C$ が推定できると $\lambda_j$, $v_j$ も推定することができます.$\{\hat{\lambda}_j\}$, $\{\hat{v}_j\}$ をそれぞれ $\hat{C}$ の固有値,固有関数とすると,適当な条件のもとで
E\left[\max_{1 \leq j \leq q}|\hat{\lambda}_{j} - \lambda_{j}|^{2}\right] = O\left({1 \over T}\right),\ E\left[\max_{1 \leq j \leq q}\|\hat{c}_j\hat{v}_{j} - v_{j}\|^{2}\right] = O\left({1 \over T}\right)\ (\text{$q \geq 1$ は固定})
であることが示せます.ここで $\hat{c}_j = \text{sign}(\langle \hat{v}_j,v_j\rangle)$ です.
上記の結果より,$\hat{v}_j$ で $v_j$ を推定する場合,向き(sign)については正しく推定できないため,この結果を統計分析に用いる場合,$v_j$ の向きに依存しない方法を使う必要があることに注意しておきます.
FPCA を用いることにより,オリジナルのデータ(無限次元)のもつ情報のロスをできるだけ抑えつつ(有限次元データの枠組みで)データ分析を行うことができるようになります.FPCA については fda など R で利用可能なパッケージが公開されているので,関数データの生成から $\hat{C}$, $\{\lambda_j\}$, $\{v_j\}$ の計算まで実行できるようになっています.
気温データの分析
関数データ解析の例として,fda パッケージを利用してカナダの気温データを分析してみます.まず下の図は35個の関数データをプロットした図にそれらを平均した関数(黒い太線)をプロットしたものです.
library(fda)
# Canadian weather data
daybasis365 <- create.fourier.basis(c(0,365),365)
# Prepare functional data
harmLfd <- vec2Lfd(c(0,(2*pi/365)^2,0), c(0, 365))
tempfdPar <- fdPar(daybasis365,harmLfd,1e4)
tempfd <- smooth.basis(1:365,daily$tempav,tempfdPar)
# Compute eigenvalues and eigenfunctions
temppca <- pca.fd(tempfd$fd,nharm=4) #nharm: number of principal components
plot(tempfd$fd,xlab="day",ylab="temperature",cex.lab=1,cex.axis=1)
lines(temppca$meanfd,lwd=5,col=1)
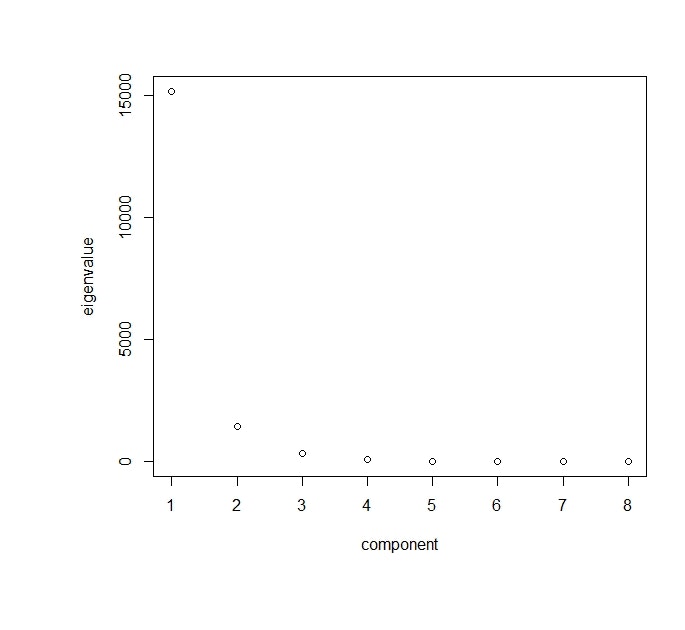
次にデータから固有値を計算してみます.計算結果が下の図です.結果を見ると4番目の固有値以降はほぼゼロとなっていて,第4主成分までみればほぼデータの情報を損なうことなく分析できそうだということがわかります.
plot(temppca$values[1:8],xlab='component',ylab='eigenvalue',col="black",
cex.lab=1,cex.axis=1,cex=1)
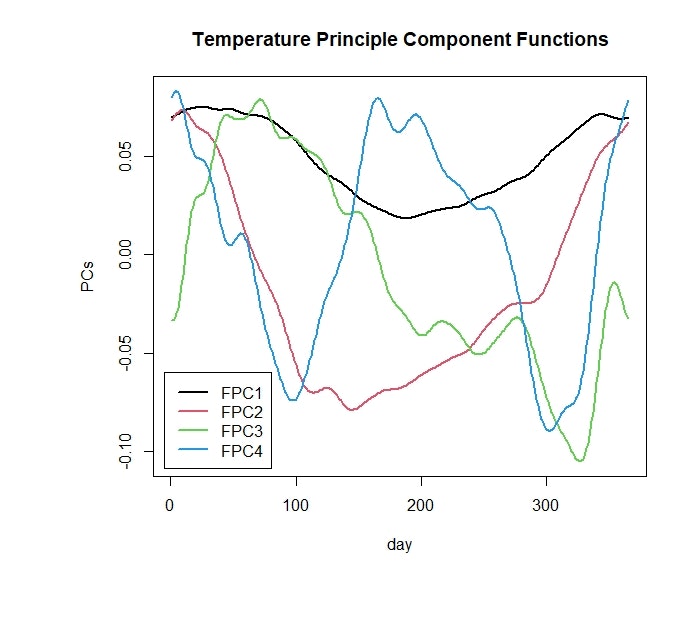
第1~4主成分までをプロットしたものが下の図です.
matplot(1:365,harmvals,xlab='day',ylab='PCs',
lwd=2,lty=1,cex.lab=1,cex.axis=1,type='l')
legend(-5,-0.06,c('FPC1','FPC2','FPC3','FPC4'),col=1:4,lty=1,lwd=2)
title('Temperature Principle Component Functions')
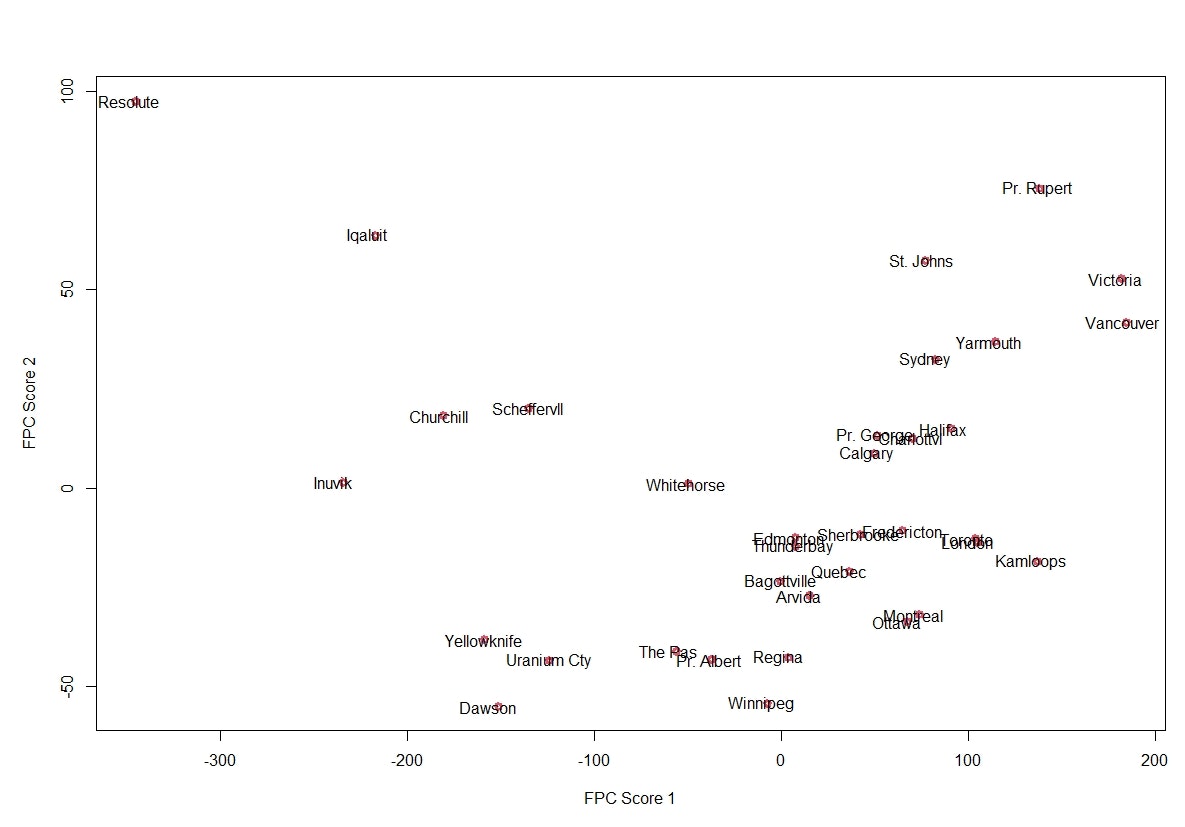
さらに35の都市それぞれについて,第1主成分,第2主成分に対応するFPCスコアをプロットすると以下の図のようになります.FPCスコアをプロットすることでいくつかわかることがあります.例えば Inuvik では第2主成分のFPCスコアはほぼゼロになっていますが,これは第2主成分はほぼ寄与しないことを示しています.FPCスコアの解釈についても通常の主成分分析と同様です.
plot(temppca$scores[,1:2],xlab='FPC Score 1',ylab='FPC Score 2',col=2,lwd=3,
cex.lab=1,cex.axis=1,cex=1)
text(temppca$scores[,1],temppca$scores[,2],labels=daily$place,cex=1)
FPCAの応用例
以下ではFPCAを利用した関数時系列データの統計分析手法を紹介します.ここでは統計分析でよく取り上げられる2標本問題と時系列解析において重要な問題である将来の値の予測について取り上げます.FPCAの説明のところで,データから計算される共分散オペレーター $\hat{C}$ の固有関数 $\hat{v}_j$ で $v_j$ を推定する場合,$v_j$ の向き(sign)については正しく推定できないため,この結果を統計分析に用いる場合には $v_j$ の向きに依存しない方法を使う必要があると書きましたが,以下で紹介する2つの方法は何れも$v_j$ の向きに依存しない方法になっています.
2標本検定
Horvath et al.(2013) では独立な2つの関数時系列データ $\{X_{1,t}\}_{t \in \mathbb{Z}}$, $\{X_{2,t}\}_{t \in \mathbb{Z}}$ がそれぞれロケーションモデル
\begin{align}
X_{1,t} &= m_{1} + v_{1,t},\\
X_{2,t} &= m_{2} + v_{2,t}
\end{align}
に従う場合に
\mathbb{H}_0: \|m_{1} - m_{2}\|=0\ \text{vs.}\ \mathbb{H}_1: \|m_{1} - m_{2}\|>0
をそれぞれの観測値 $\{X_{1,t}\}_{t=1}^{T_1}$, $\{X_{2,t}\}_{t=1}^{T_2}$ (${T_1 \over T_1 + T_2} \to \theta \in (0,1)$, $\min\{T_1, T_2\} \to \infty$) を用いて検定する方法が提案されています.ただし,$\{v_{1,t}\}$, $\{v_{2,t}\}$ は平均ゼロの独立な(定常)関数時系列,$m_{1}$,$m_{2} \in H$ は $X_{1,t}$, $X_{2,t}$ の平均関数.ここでは彼らのアイデアを簡単に紹介します.
まずいくつか記号を導入しておきます.
$C_1$, $C_{2}$ をそれぞれ $\{X_{1,t}\}$, $\{X_{2,t}\}$ の 共分散オペレーターとし,
$D = (1-\theta)C_{1} + \theta C_{2}$, さらに $\{\eta_j\}$, $\{\nu_j\}$ を $D$ の固有値,固有関数とします.
\hat{C}_j={1 \over T}\sum_{t=1}^{T}X_{j,t} \otimes X_{j,t}\ (j=1,2),
$\hat{\theta} = {T_1 \over T_1 + T_2}$ として $\{\hat{\eta}_j\}$, $\{\hat{\nu}_j\}$ を $\hat{D} = (1-\hat{\theta})\hat{C}_{1} + \hat{\theta}\hat{C}_{2}$ の固有値,固有関数とします.検定統計量を
U_{T_1,T_2}:={T_1 T_2 \over T_{1} + T_{2}}\|\bar{X}_{1,T} - \bar{X}_{2,T}\|^2 = {T_1 T_2 \over T_{1} + T_{2}}\sum_{j=1}^{\infty}\langle \bar{X}_{1,T} - \bar{X}_{2,T}, \nu_{j} \rangle^{2}
で定義すると適当な条件の下で以下が成り立ちます:
\begin{align}
U_{T_1,T_2}&
\begin{cases}
\stackrel{d}{\to} \sum_{j=1}^{\infty}\eta_{j}N_{j}^{2}=: U_{\infty,\infty} & \text{under $\mathbb{H}_0$},\\
\stackrel{p}{\to} \infty & \text{under $\mathbb{H}_1$}.
\end{cases}
\end{align}
ここで $\{N_{j}\}$ は独立な標準正規分布に従う確率変数列です.検定を実行するにあたり,$U_{\infty,\infty}$ の分位点を推定する必要がありますが,漸近分布 $U_{\infty,\infty}$ は無限和で表されるため厳密にその分位点を計算することができません.実用上は上記の無限和の表現をFPCAを用いて有限次元に還元した検定統計量とその漸近分布
\bar{U}_{T_1,T_2}:={T_1 T_2 \over T_{1} + T_{2}}\sum_{j=1}^{q}\hat{\eta}_{j}^{-1}\langle \bar{X}_{1,T} - \bar{X}_{2,T}, \hat{\nu}_{j}\rangle^2
\begin{cases}
\stackrel{d}{\to} \sum_{j=1}^{q}N_{j}^{2} \sim \chi^{2}(q) & \text{under $\bar{\mathbb{H}}_0$},\\
\stackrel{p}{\to} \infty & \text{under $\bar{\mathbb{H}}_1$}.
\end{cases}
を利用します.ここで $\chi^{2}(q)$ は自由度 $q$ のカイ2乗分布で,
\bar{\mathbb{H}}_0: \max_{1 \leq j \leq q}\langle m_{1} - m_{2}, \nu_j \rangle^{2} = 0\ \text{vs.}\ \bar{\mathbb{H}}_1: \max_{1 \leq j \leq q}\langle m_{1} - m_{2}, \nu_j \rangle^{2}>0
です.ここでのポイントはFPCAを用いることにより検定統計量の漸近分布が未知パラメータに依存せず,さらにオリジナルのデータの情報のロスを抑えつつ検定が実行可能になっている点です.
予測
Aue et al.(2015)では FPCA を用いた関数時系列データの予測方法が提案されています.ここでは彼らのアイデアを簡単に紹介します.
$X=\{X_{t}\}_{t \in \mathbb{Z}}$ を関数時系列データとし,$X_{1},\cdots,X_{T}$ を観測値とします.また $\{\lambda_j\}$, $\{v_j\}$ を $X$ の共分散オペレーター $C$ の固有値,固有関数とします.さらに $\hat{C}$, $\{\hat{\lambda}_j\}_{j=1}^{q}$, $\{\hat{v}_j\}_{j=1}^{q}$ をそれぞれ $C$, $\{\lambda_j\}_{j=1}^{q}$, $\{v_j\}_{j=1}^{q}$ の推定値とします.これらは FPCA を用いて計算できます.観測値 $X_{1},\cdots,X_{T}$ をもとに $X_{T+k}$ を予測する ($k$-step ahead prediction) 方法は以下の通りです:
(Step1) $X_{t}$ の FPC スコア
\hat{\boldsymbol{X}}_t = (\langle X_{t}, \hat{v}_1 \rangle,\cdots,\langle X_{t}, \hat{v}_q \rangle)',\ t=1,\cdots,T
を計算.
(Step2) FPCによって得られた $q$-次元のベクトル $\hat{\boldsymbol{X}}_t$, $t=1,\cdots, T$ に対してベクトル値自己回帰モデル(vector autoregressive model, VAR) を当てはめる.
\hat{\boldsymbol{X}}_t = \Psi_{1}\hat{\boldsymbol{X}}_{t-1} + \cdots + \Psi_{1}\hat{\boldsymbol{X}}_{t-p} + \boldsymbol{\varepsilon}_t,\ t=p,\cdots,T.
VAR モデルについては FitAR などの R のパッケージで Durbin-Levinson アルゴリズムを用いて $k$ 期先の予測値 $\hat{\boldsymbol{X}}_{T+k}= (\hat{X}_{T+k}^{(1)},\cdots, \hat{X}_{T+k}^{(q)})'$ を計算することができます.
(Step3) (Step2) で求めた $\hat{\boldsymbol{X}}_{T+k} $ と $\{\hat{v}_j\}_{j=1}^{q}$ から,Karhunen-Loeve 展開を用いて最終的な関数データの予測値 $\tilde{X}_{T+k}$ を計算:
\tilde{X}_{T+k} = \sum_{j=1}^{q}\langle \hat{X}_{T+k}^{(j)}, \hat{v}_j \rangle \hat{v}_j.
Aue et al.(2015)では他にも VAR モデルのラグ $p$ と予測に利用するFPCスコアの数 $q$ の選び方についても議論されています.
文献紹介
関数データ解析についてより詳しく知りたい方のためにいくつか参考文献を挙げておきます.
- Bosq(2000): 関数時系列データ解析の理論的妥当性に焦点を当てたテキストです.時系列解析の知識に加え,ヒルベルト空間やバナッハ空間などの関数解析の知識が必要なので上級者向けです.
- Ramsay and Silverman(2005): 関数データ解析の有名なテキストです.特に多変量解析でのPCAと関数データ解析におけるFPCAとの関係について詳しく書かれています.
- Ferraty and View(2006): 関数データ・関数時系列データに対するノンパラメトリックな統計分析の手法について解説されたテキストです.ノンパラメトリックな回帰モデルや分類について書かれた数少ない文献です.
- Horvath and Kokoszka(2012): 関数データ・関数時系列データのテキストで,特に関数時系列データに対する分析手法について著者たちが開発したより現代的な方法が解説されています.
まとめ
この記事では関数時系列データに対する主成分分析 (FPCA) とそれを利用した2標本検定と予測について紹介しました.続編の「関数時系列データの主成分分析(2)【研究紹介】」では今回紹介した関数(時系列)データ分析の方法を非定常な関数時系列データに拡張する方法について解説します.さらに「関数時系列データの主成分分析(3)」では関数時系列データの予測について実際のデータ分析の例を紹介する予定です.
株式会社Nospareには統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.

参考文献
[1] Aue, A., Dubart Norinho, D. and Hormann, S. (2015). On the prediction of stationary functional time series. Journal of the American Statistical Association. 110, 378-392.
[2] Bosq, D. (2000). Linear Processes in Functional Spaces. Springer.
[3] Ferraty, F. and View, P. (2006). Nonparametric Functional Data Analysis. Springer.
[4] Horvath, L. and Kokoszka, P. (2012). Inference for Functional Data with Applications. Springer.
[5] Horvath, L., Kokoszka, P., and Reeder, R. (2013). Estimation of the mean of functional time series and a two-sample problem. Journal of the Royal Statistical Society Series B. 75, 103-122.
[6] Li, D., Robinson, P., and Shang, H. L. (2020). Long-range dependent curve time series. Journal of the American Statistical Association. 115, 957-971.
[7] Ramsay, J. O. and Silverman, B. W. (2005). Functional Data Analysis. Springer.