はじめに
東京大学/株式会社Nospare リサーチャーの栗栖です.
この記事は最近の研究成果「空間データに対する局所多項式トレンド回帰」(Kurisu and Matsuda(2024))についての解説記事の続編です.本研究の目的についての説明はこちらの記事を参照してください.前回の記事では局所多項式回帰推定量 (local polynomial (LP) estimator) の信頼区間の構成方法について紹介しましたが,この記事では数値実験の結果を通して実際に local linear (LL) 推定量の信頼区間のパフォーマンスを見てみようと思います.
データ生成過程
2次元の空間 $R = [-5,5]^2$ 内の地点 $\boldsymbol{X}_i=(X_{1,i},X_{2,i})'$, $i=1,\dots,1000$ において空間データ $Y_i = Y(\boldsymbol{X}_i)$を観測する状況を考えます.ここで,$\boldsymbol{X}_i$は$[-5,5]^2$上の一様分布から発生させています.このとき,データ $(Y_i, \boldsymbol{X}_i)$が以下の回帰モデルに従うとします:
\begin{align*}
Y_i &= m(\boldsymbol{X}_i) + \underbrace{e(\boldsymbol{X}_i) + \varepsilon_i}_{\text{誤差項}=:V_i},\ i=1,\dots,1000.\\
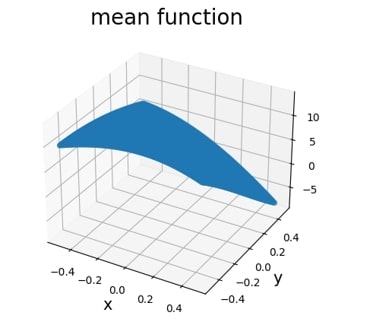
m(\boldsymbol{X}_i) &=(10X_{1,i}+15)\cos(X_{1,i} + X_{2,i}+1).
\end{align*}
ここで,$\boldsymbol{e}=\{e(x): x \in \mathbb{R}^2\}$ は空間相関をもつ誤差項で,データ$Y_i$ の空間データとしての構造を表現する部分です.特に以下のモデルから$\boldsymbol{e}$を生成します.
\boldsymbol{e}(\boldsymbol{x}) = \sum_{j = 1}^{800}Z_je^{-\lambda \|\boldsymbol{x}-\boldsymbol{a}_j\|},\ \boldsymbol{x}\in\mathbb{R}^2,\ \lambda>0.
ここで,$Z_j$ は独立同分布で平均$0$, 分散$\tau^2$の正規分布,$\{\boldsymbol{a}_j\}$は$[-5,5]^2$上の一様分布から独立に発生させています.また観測誤差$\varepsilon$は独立同分布で平均$0$, 分散$\sigma^2$の正規分布に従う変数です.ここで用いた誤差項のモデルは連続型AR(1)(continuous AR(1))確率場と呼ばれ,時系列データのモデルとして用いられる自己回帰過程を自然に空間データに拡張したモデルとなっていることが知られています.
データ生成過程の回帰関数は以下の図のような形をしています(図において $x$軸を$X_1$,$y$軸を$X_2$に関する値と読み替えてください).
上記のモデルをもとに,誤差項に関して以下の3パターンのシナリオの下でLL推定量の漸近的性質が成立しているか確認してみます.
- Case(i), 誤差項が空間相関をもたない(=誤差項が独立な)場合:$V_i = \varepsilon_i$, $\sigma^2=1$
- Case(ii), 誤差項が空間相関をもつ場合:$V_i = e(\boldsymbol{X}_i) + \varepsilon_i$, $(\lambda, \tau^2, \sigma^2)=(1,0.1^2,0.1^2)$
- Case(iii), 誤差項が空間相関をもつ場合:$V_i = e(\boldsymbol{X}_i) + \varepsilon_i$, $(\lambda, \tau^2, \sigma^2)=(0.5,0.05^2,0.1^2)$.
Case(ii), Case(iii) の違いとして,Case(iii)の方がより空間相関が強い(相関を計算する2点が離れていくときの相関係数の減衰の速さがより遅い)モデルとなっています.
またLL推定量の計算にあたり,以下のカーネル関数を用います.
K(x_1,x_2) = (1-|x_1|)(1-|x_2|), |x_1|\leq 1,\ |x_2|\leq 1.
さらにL推定量のバンド幅として$h=0.25$, LL推定量の分散の推定量の計算に必要な
バンド幅を$h=0.25$, $b=8$とします.
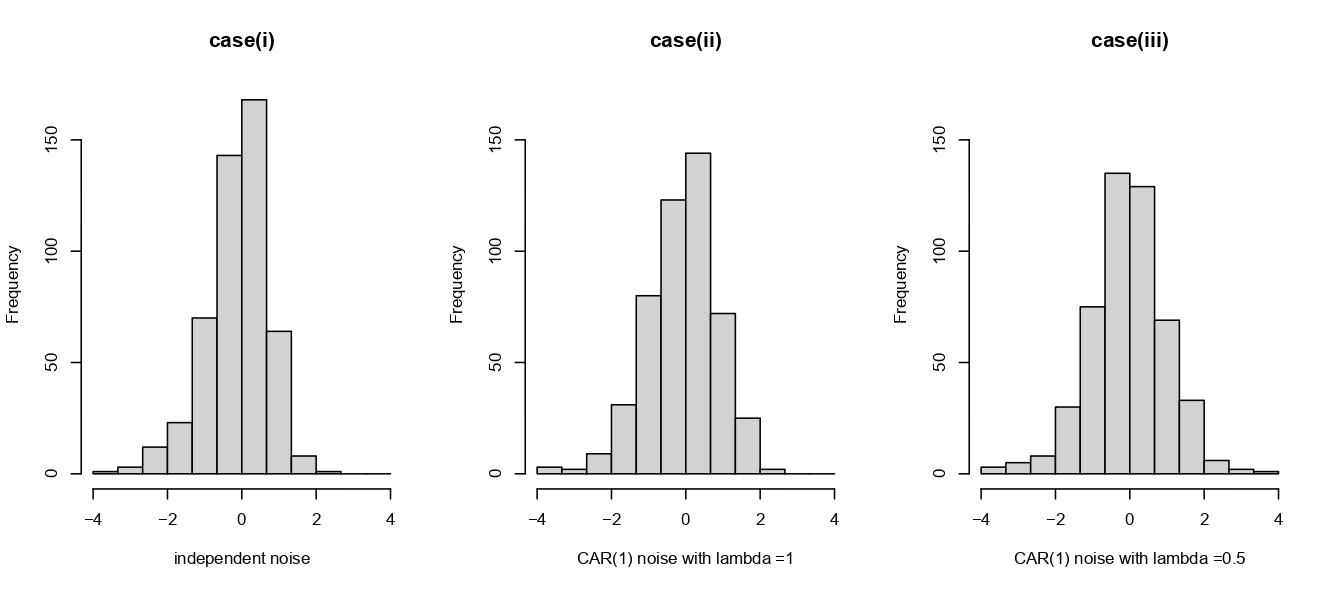
正規化したLL推定量のヒストグラム
上記の設定の下で,$m(0,0)$をLL推定量で推定してみましょう.以下の図はCase(i)-(iii)それぞれのシナリオに対して,正規化したLL推定量
\hat{T} = {\hat{m}(0,0) - m(0,0) - \text{bias} \over \sqrt{\hat{W}_n(0,0)}}
を500回繰り返し計算し,そのヒストグラムを描いたものです.ここで,$\hat{W}_n(0,0)$はLL推定量の分散の推定量であり,$\hat{T}$ は $\hat{W}_n(0,0)$ と bias を用いて正規化したLL推定量のもつバイアスを修正しています.ここで,バイアス項には回帰関数 $m$ の2階の偏微分 ($\partial^2 m(0)/\partial x_1^2$, $\partial^2 m(0)/\partial x_2^2$) が含まれますが,これらの値の推定には local quadratic (LQ) 推定,すなわち局所的に2次の多項式で回帰関数 $m$ を近似して推定を行っています.またLQ推定の際に必要となるバンド幅は$h = 0.25$と設定しています.LL推定量の具体的な分散の形とその推定,バイアスの形については前回の記事を参照してください.
この結果から,誤差項に空間相関がある場合,ない場合のいずれの場合においても正規化したLP推定量のヒストグラムは標準正規分布でよく近似できることがわかり,理論的な結果と整合的であることが確認できます.
LP推定量の信頼区間の経験被覆率
さらにLP推定量を用いて$m(0,0)$の95%信頼区間を500回計算し,その経験被覆率
(\text{経験被覆率}) = {(500回中信頼区間の中にm(0,0)が含まれていた回数) \over 500}
を計算してみましょう.以下のテーブルは500回繰り返し計算した正規化したLL推定量の平均(mean),分散(variance),経験被覆率(empirical coverage probability)をまとめたものです.
| Case | mean | variance | coverage |
|---|---|---|---|
| (i) | -0.199 | 1.012 | 0.944 |
| (ii) | -0.179 | 1.517 | 0.948 |
| (iii) | -0.120 | 1.380 | 0.940 |
上記の結果において,理想的にはmeanは$0$に近く,varianceは$1$に近いほど理論的な結果に近いという解釈が可能です.シナリオにより理論との多少のずれがありますが,これは数値実験において(シナリオ間のフェアな比較を行うために)LL推定量のバンド幅を決め打ちで行ったことによる影響だと思われます.実際のデータ分析では平均二乗誤差(mean squared error,MSE)最小化などのルールを用いてバンド幅を選択することになります.経験被覆率(coverage)に関してはどのシナリオに対しても理想的な値 $0.95$に近い値となっており,適切な信頼区間が構成できていることが確認できます.
まとめ
この記事では空間データに対するノンパラメトリック回帰分析に関して,最近の研究成果である Kurisu and Matsuda (2024) の数値実験の結果を紹介しました.株式会社Nospareにはノンパラメトリック分析や空間統計に限らず,統計学の様々な分野を専門とする研究者が所属しています.統計アドバイザリーやビジネスデータ分析につきましては株式会社Nospareまでお問い合わせください.

参考文献
[1] Kurisu, D. and Matsuda, Y. (2024) Local polynomial trend regression for spatial data on $\mathbb{R}^d$. arXiv:2211.13467. Bernoulli 30, 2770-2794.