空間データのためのブートストラップ法(データ分析編２)

空間データのためのブートストラップ法

横浜国立大学/株式会社Nospare の栗栖です．

この記事は
「空間データのためのブートストラップ法(解説編)」
「空間データのためのブートストラップ法(データ分析編１)」
の続編です．
前回の記事 (「空間データのためのブートストラップ法(データ分析編１)」) では空間データ・時空間データ分析に関する最近の研究成果 (Kurisu, Kato and Shao(2024)) で提案した空間ワイルドブートストラップ(spatially dependent wild bootstrap, SDWB)の数値実験の結果とアメリカの降水量データの分析への応用について解説しました．この記事では (データ分析編１) の続きとして，空間データに適用可能なブートストラップ法としてLahiri and Zhu(2006)で提案されたグリッドベースブロックブートストラップ(grid-based block bootstrap, GBBB)とのパフォーマンスを比較した数値実験の結果について紹介します．

数値実験

データ生成過程

(データ分析編１)と同様に，以下のモデルから数値実験のデータを生成します：

\boldsymbol{Y}(\boldsymbol{s}_{i}) = (Y_1(\boldsymbol{s}_{i}),\dots,Y_p(\boldsymbol{s}_{i}))' = A\boldsymbol{F}(\boldsymbol{s}_{i}) + \boldsymbol{R}(\boldsymbol{s}_{i}),\ i=1,\cdots,n,

$A = (A_{j,k})$：$p \times 5$ 行列，$A_{j,k}$ は独立に $[-1,1]$ 上の一様分布から生成，
$\boldsymbol{F}$：各成分が独立な平均 $\boldsymbol{0}$ の $5$-変量ガウス過程，$\boldsymbol{F}(\boldsymbol{s}) = (F_{1}(\boldsymbol{s}),\cdots,F_{5}(\boldsymbol{s}))'$，$\boldsymbol{s} \in \mathbb{R}^{2}$．
特に $F_{j}$ は全て以下の共分散関数をもつとします¹：
　

\text{Cov}(F_{j}(\boldsymbol{s}), F_{j}(\boldsymbol{0})) = (3\|\boldsymbol{s}\|+1)e^{-3\|\boldsymbol{s}\|}, \|\boldsymbol{s}\|=\sqrt{s_{1}^{2} + s_{2}^{2}}

$\boldsymbol{R}(\boldsymbol{s}_{i})$：$p$-変量の標準正規分布に従う独立同分布な観測誤差．
$n \in \{100, 250\}$，$p \in \{10,100,400\}$，$\lambda_{n} \in \{15,25\}$．
$\boldsymbol{s}_{i} \in R_{n} = \lambda_n[-1/2, 1/2]^{2}$，

$\boldsymbol{s}_{i}$のパターンとして以下の2パターンを考えます．
(1) uniform：独立に $R_{n}$ 上の一様分布から生成．
(2) Gauss：独立に2次元の正規分布 $N((-1/4,-1/4)', 5/4I_2)$ から生成して各成分を $\lambda_n$ 倍する．(ただし正規分布は$[-1/2,1/2]^2$で打ち切った値を生成)
ここで，(2)のパターンは空間データに"hot spot"(データの観測地点が集中している地域)がある場合を想定したパターンに対応しています．
空間ワイルドブートストラップの実装に必要になるガウス過程のカーネル関数としては

a(x) = 
\begin{cases}
1-|x| & \text{$|x|\leq 1$ のとき} \\
0 & \text{それ以外}
\end{cases}

さらに $b = 1,2,\cdots ,10$ とします．

SDWBの計算

解説編でも書きましたが，SDWBの計算方法についてもう一度確認しておきます．

(Step1) 標本平均 $\overline{\boldsymbol{Y}}_{n} = {1 \over n}\sum_{i=1}^{n}\boldsymbol{Y}(\boldsymbol{s}_{i})$ と $\hat{\Sigma}^{\boldsymbol{V}_{n}}$ を計算：

\hat{\Sigma}^{\boldsymbol{V}_{n}} = {1 \over n^{2}\lambda_{n}^{-d}}\sum_{i_{1}, i_{2} = 1}^{n}(\boldsymbol{Y}(\boldsymbol{s}_{i_{1}}) - \overline{\boldsymbol{Y}}_{n})(\boldsymbol{Y}(\boldsymbol{s}_{i_{2}}) - \overline{\boldsymbol{Y}}_{n})'a\left({\boldsymbol{s}_{1} - \boldsymbol{s}_{2} \over b_{n}}\right) 

(Step2) ブートストラップ標本の数 $B$ を設定し，共分散行列 $A = (a(\boldsymbol{s}_{i}-\boldsymbol{s}_{k})/b_{n}))_{1 \leq i,k \leq n}$ をもつ平均 $\boldsymbol{0}$ の $n$ 次元正規分布に従う変数 $\boldsymbol{W}^{(1)}$$,\dots,$ $\boldsymbol{W}^{(B)}$ を生成：

\boldsymbol{W}^{(k)} = (W_{1}^{(k)},\dots,W_{n}^{(k)})',\ k=1,\dots, B.

(Step3) ブートストラップ標本 $\mathcal{Y}^{(1)}_{n}, \dots, \mathcal{Y}^{(B)}_{n}$ を生成：

\begin{align}
\mathcal{Y}^{(k)}_{n} &= \{\boldsymbol{Y}^{(k,\ast)}(\boldsymbol{s}_{1}),\dots, \boldsymbol{Y}^{(k,\ast)}(\boldsymbol{s}_{n})\},\\
\boldsymbol{Y}^{(k,\ast)}(\boldsymbol{s}_{i}) &= \overline{\boldsymbol{Y}}_{n} + \left(\boldsymbol{Y}(\boldsymbol{s}_{i} ) - \overline{\boldsymbol{Y}}_{n}\right)W^{(k)}_{i},\ k=1,\dots,B.
\end{align}

(Step4) ブートストラップ標本 $\mathcal{Y}_{n}^{(k)}$ ごとに

T_{n}^{(k)} = \sqrt{\lambda_{n}^{d}}\max_{1 \leq j \leq p}\left|{\overline{Y}_{j,n}^{(k,\ast)} - \overline{Y}_{j,n} \over \sqrt{\hat{\Sigma}_{j,j}^{\boldsymbol{V}_{n}}}}\right|,\ k=1,\dots, B

を計算して $T_{n}^{(1)},\dots, T_{n}^{(B)}$ の経験分布から分位点 $q_{n}(1-\tau)$ の推定値 $\hat{q}_{n}(1-\tau)$ を計算．

ここではGBBBの計算方法については述べませんが，詳しく知りたい方は Lahiri and Zhu(2006) を参照してください．
GBBBではブートストラップの計算を行うために (a) 観測領域 $R_n$ を小さな長方形に分割し，(b) それぞれの長方形をランダムに移動させ，(c) 移動先の領域に含まれる観測地点でのデータを利用してブートストラップサンプルを生成します．このため，(1) $R_n$が複雑な形になるほど長方形での分割が難しくなり，(2) 細かく分割するほど計算コストが大きくなるという問題が生じます．一方でSDWBではこのような問題は生じません．従ってSDWBはGBBBに比べて実装が簡単であるという利点があります．

数値実験の結果

以下の図は上記のデータ生成過程から得られたデータをもとにSDWBとGBBBを利用して $p$ 次元ベクトルの標本平均 $\overline{\boldsymbol{Y}}_{n} = {1 \over n}\sum_{i=1}^{n}\boldsymbol{Y}(\boldsymbol{s}_{i})$ の 95% 信頼区間を1000回繰り返し計算し，　

{\text{1000回中 $p$ 個の信頼区間がすべて $0$ を含んでいた回数} \over 1000}

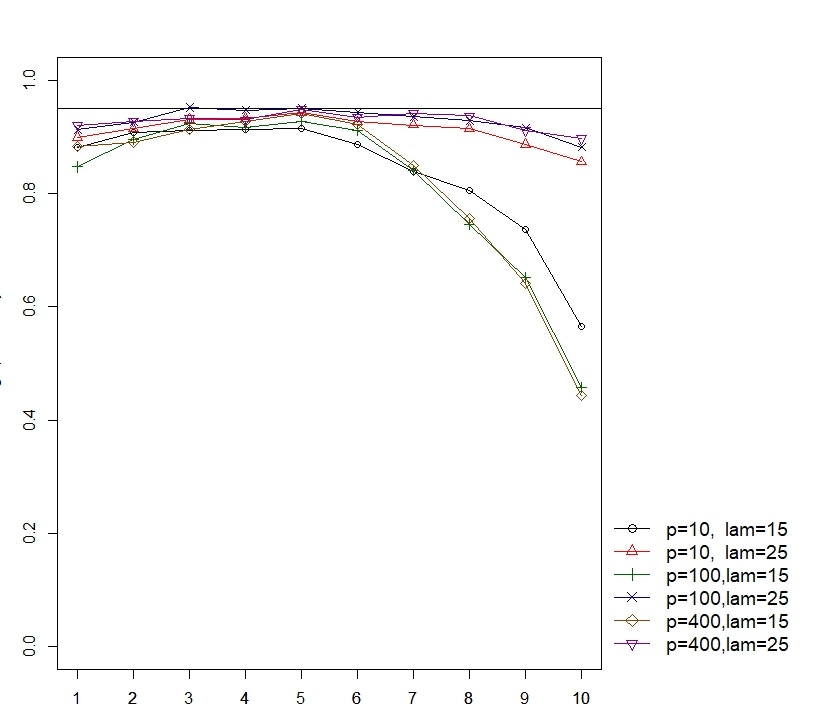
(経験被覆確率，empirical coverage probability) を計算したものです．グラフの縦軸が被覆確率，横軸はブートストラップ法の計算に必要なバンド幅 $b \in \{ 1,\dots,10 \}$ に対応しています．この例ではSDWB, GBBBともにブートストラップ標本の数 $B = 1500$ としました．今回は95%信頼区間を計算してるので，図の中の折れ線が黒の横線 (coverage probability = 0.95) に近いほどパフォーマンスが良いことを示しています．

下の6つの図はそれぞれ
1番目：SDWBの結果, n=100, uniform
2番目：SDWBの結果, n=100, Gauss
3番目：SDWBの結果, n=250, uniform
4番目：GBBBの結果, n=100, uniform
5番目：GBBBの結果, n=100, Gauss
6番目：GBBBの結果, n=250, uniform
に対応しています．

以下の結果より，

• SDWB, GBBB何れもサンプルサイズ $n$ が増加してもあまりパフォーマンスは変わらないが $\lambda_n$ が増加するとパフォーマンスが向上する．
• SDWB, GBBB何れも観測地点が Gauss (non-uniform) の場合は uniform の場合と比べてパフォーマンスがバンド幅 $b$ の選び方に敏感になる．
• SDWBはSGBBBに比べてバンド幅の選択に対して頑健である．
• 全体としてSDWBはGBBBと比べて良いパフォーマンスを示す．

ということがわかります．

論文の中では他の数値実験の結果についても報告していますので興味のある方はご参照ください．

まとめ

この記事では Kurisu, Kato and Shao(2024) で提案したSDWBとGBBBのパフォーマンスの比較した数値実験の結果を紹介しました．
株式会社Nospareには空間統計・時空間統計に限らず，統計学の様々な分野を専門とする研究者が所属しております．統計アドバイザリーやビジネスデータの分析につきましては 株式会社Nospare までお問い合わせください．

参考文献
[1] Kurisu, D., Kato, K. and Shao, X. (2024). Gaussian approximation and spatially dependent wild bootstrap for high-dimensional spatial data. Journal of the American Statistical Association 119, 1820-1832.
[2] Lahiri, S.N. and Zhu, J. (2006). Resampling methods for spatial regression models under a class of stochastic designs. Annals of Statistics 34, 1774-1813.

1. 今回の数値実験で用いたガウス過程 $\boldsymbol{F}$ ような，2 点間の距離の指数関数で減衰するような共分散構造をもつ空間過程は Matern クラスと呼ばれ，空間統計では非常によく利用されるモデルです． ↩