はじめに
最終的に、9x9 数独の答えになる組み合わせを調べようとしていますが、膨大な数になることが予想されます。
このため、まずは小さな数独での組み合わせを調べるソースコードを考え、そこから改良する方針で進めます。
この記事では、4x4と6x6の数独の答えになる組み合わせを調べる実装例を紹介します。
4x4の数独
手始めに、4x4の数独の答えになる組み合わせを調べる方法を実装しました。
処理時間短縮の工夫
組合せを調べる際、似たようなパターンが数多く出現します。
これらのパターンの調査を省略することで、処理時間を大幅に短縮することができます。
法則1:数字は交換が可能
最初に思いついたのが、数独の答えになる組み合わせを1つ見つけると、その答えの数字を入れ替えても答えとして成立するということです。
例えば、図1が答えとして成立すれば、図1の数字を入れ替えた図2も答えとして成立します。
図2は図1の1と2を交換したものです。
ということで、まずは、以下の図の条件を満たすABCDの組合せが何通りあるかを調べます。
ABCDと1234を対応付ける組合せは、4! = 24通りあります。
つまり、A = 1、B = 2、C = 3、D = 4での組合せの数を調べ、24倍するとすべての組合せの数になります。
これで、処理時間を24分の1に短縮できます。
ソースコード
A = 1、B = 2、C = 3、D = 4とした場合の組合せの数を調べる方法の実装例です。
import std.datetime;
import std.stdio;
const NUM = 4;
const ROW = NUM;
const COL = NUM;
const BLOCK_ROW = 2;
const BLOCK_COL = NUM / BLOCK_ROW;
ubyte[COL][ROW] rect;
bool[NUM][ROW] yoko;
bool[NUM][COL] tate;
bool[NUM][BLOCK_COL][BLOCK_ROW] block;
long starttime;
long count;
bool push(int x, int y, int n)
{
if ( yoko[y][n] == false
&& tate[x][n] == false
&& block[y / BLOCK_COL][x / BLOCK_ROW][n] == false ){
rect[y][x] = cast(ubyte)(n + 1);
yoko[y][n] = true;
tate[x][n] = true;
block[y / BLOCK_COL][x / BLOCK_ROW][n] = true;
return ( true );
}
return ( false );
}
void pop(int x, int y, int n)
{
rect[y][x] = 0;
yoko[y][n] = false;
tate[x][n] = false;
block[y / BLOCK_COL][x / BLOCK_ROW][n] = false;
}
bool next(ref int x, ref int y)
{
if ( x == COL - 1 ){
if ( y == ROW - 1 ){
count++;
writefln("--%03d--\n%(%(%d %)\n%)", count, rect);
return ( false );
} else {
x = 0;
y++;
}
} else {
x++;
}
return ( true );
}
void solve(int x, int y)
{
if ( rect[y][x] > 0 ){
if ( next(x, y) ){
solve(x, y);
}
return;
}
for ( int n = 0; n < NUM; n++ ){
if ( push(x, y, n) ){
int x0 = x;
int y0 = y;
if ( next(x, y) ){
solve(x, y);
}
x = x0;
y = y0;
pop(x, y, n);
}
}
}
void main()
{
rect = [[1, 2, 3, 4],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]];
for ( int y = 0; y < ROW; y++ ){
for ( int x = 0; x < COL; x++ ){
if ( rect[y][x] > 0 ){
if ( push(x, y, rect[y][x] - 1) == false ){
writeln("Illegal initial value");
return;
}
}
}
}
starttime = Clock.currStdTime();
solve(0, 0);
long time = (Clock.currStdTime() - starttime) / 10_000;
writefln("time = %,3d ms", time);
writefln("answer = %,3d", count);
writefln("total = %,3d", 24 * count);
}
D:\Dev> ldc2 -m64 -release -O sudoku44.d
D:\Dev> sudoku44
--001--
1 2 3 4
3 4 1 2
2 1 4 3
4 3 2 1
・・・省略・・・
--012--
1 2 3 4
4 3 2 1
3 4 1 2
2 1 4 3
time = 15 ms
answer = 12
total = 288
A = 1、B = 2、C = 3、D = 4とした場合の組合せの数は、12通りであることがわかりました。
結果として、4x4の数独の答えになる組み合わせは、288通り(= 12 x 4!)であることがわかりました。
6x6の数独
6x6の数独は、3x2のブロックが6つある形になります。以下は、組み合わせ例です。
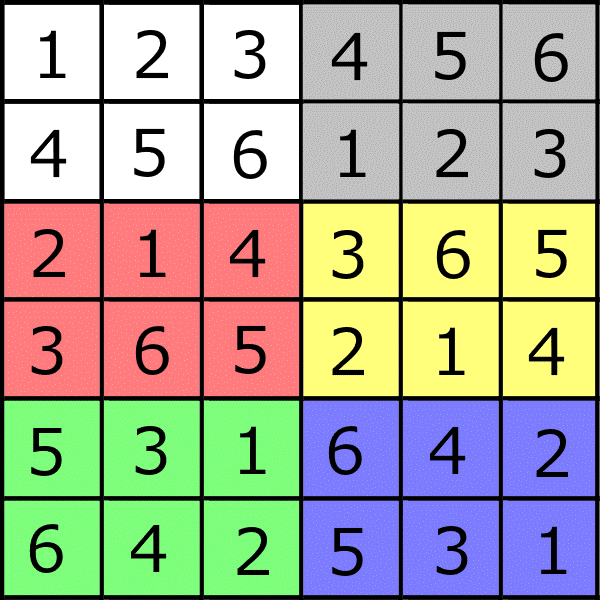
ソースコードsudoku44.dの定数の値を変えるだけで、6x6の組み合わせを調べることができます。
import std.datetime;
import std.stdio;
const NUM = 6;
const ROW = NUM;
const COL = NUM;
const BLOCK_ROW = 3;
const BLOCK_COL = NUM / BLOCK_ROW;
// ・・・省略・・・
bool next(ref int x, ref int y)
{
if ( x == COL - 1 ){
if ( y == ROW - 1 ){
count++;
writefln("-- %05d --\n%(%(%d %)\n%)", count, rect);
return ( false );
} else {
x = 0;
y++;
}
} else {
x++;
}
return ( true );
}
// ・・・省略・・・
void main()
{
rect = [[1, 2, 3, 4, 5, 6],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0]];
for ( int y = 0; y < ROW; y++ ){
for ( int x = 0; x < COL; x++ ){
if ( rect[y][x] > 0 ){
if ( push(x, y, rect[y][x] - 1) == false ){
writeln("Illegal initial value");
return;
}
}
}
}
starttime = Clock.currStdTime();
solve(0, 0);
long time = (Clock.currStdTime() - starttime) / 10_000;
writefln("time = %,3d ms", time);
writefln("answer = %,3d", count);
writefln("total = %,3d", 720 * count);
}
D:\Dev> ldc2 -m64 -release -O sudoku66.d
D:\Dev> sudoku66 > sudoku66.txt
D:\Dev> type sudoku66.txt
-- 00001 --
1 2 3 4 5 6
4 5 6 1 2 3
2 1 4 3 6 5
3 6 5 2 1 4
5 3 1 6 4 2
6 4 2 5 3 1
・・・省略・・・
-- 39168 --
1 2 3 4 5 6
6 5 4 3 2 1
5 6 2 1 4 3
4 3 1 5 6 2
3 4 6 2 1 5
2 1 5 6 3 4
time = 165 ms
answer = 39,168
total = 28,200,960
6x6の数独の答えになる組み合わせは、28,200,960通り(= 39,168 * 6!)であることがわかりました。
8x8の数独
ソースコードsudoku44.dの定数の値を変えるだけで、答えを出すことができそうです。
ただ、そのままだと答えを出すのにおよそ9日かかりそうです。
次回以降の記事で、さらなる処理時間短縮方法を紹介できればと思います。
9x9の数独
ソースコードsudoku44.dの定数の値を変えるだけで、答えを出すことができそうです。
ただ、そのままだと答えを出すのにおよそ1200年かかりそうです。
さすがに1200年は待てないので、次回以降の記事で、さらなる処理時間短縮方法を紹介できればと思います。


