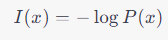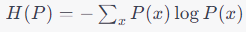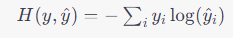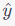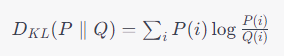自己情報量
自己情報量
自己情報量は、ある特定の事象が発生する確率に基づいて、その事象がどれだけ「驚くべき」または「予想外」であるかを測る尺度です。数学的には、事象 x の自己情報量 I(x) は以下のように定義されます。
ここで、P(x) は事象 x が発生する確率です。自己情報量は、事象が起こる確率が低いほど大きくなります。つまり、予想外の事象ほど、自己情報量は大きくなります。
エントロピー
エントロピーは、確率分布全体の「不確実性」または「予測の困難さ」を測る尺度です。自己情報量の期待値として定義されます。確率分布 P のエントロピー H(P) は以下のように定義されます。
エントロピーは、確率分布の中でどれだけ多くの事象が高い確率で発生するか、またそれらの事象がどれだけ均等に発生するかに依存します。エントロピーが高いほど、確率分布全体の予測が困難であると言えます。
交差エントロピー
交差エントロピー(Cross-Entropy)は、情報理論と機械学習の分野でよく使用される概念です。特に、分類問題の損失関数としてよく使われます。
エントロピーとは
エントロピーは、情報の不確実性や乱雑さを測る指標です。例えば、コイン投げの結果が表か裏かという2つの選択肢がある場合、どちらが出るかは完全に不確実です。このような状況のエントロピーは高いと言います。
交差エントロピーとは
交差エントロピーは、2つの確率分布の間の「違い」を測る指標です。具体的には、ある真の確率分布と、それを近似しようとするモデルの確率分布との間の違いを測ります。
数式での表現
交差エントロピーは以下の数式で表されます。
ここで、y は真の確率分布(正解ラベル)、
機械学習での利用
分類問題において、交差エントロピーは損失関数としてよく使用されます。
モデルの予測が正解に近いほど、交差エントロピーの値は小さくなります。逆に、予測が正解から遠いほど、値は大きくなります。
なぜ交差エントロピーを使うのか
交差エントロピーを使う理由は、モデルの予測が正解にどれだけ近いかを効率的に評価できるからです。予測が正解に近づくほど、損失が急速に減少し、学習が効率的に進行します。
まとめ
交差エントロピーは、2つの確率分布の間の違いを測る指標で、機械学習の分類問題でよく使用されます。モデルの予測が正解にどれだけ近いかを効率的に評価するために使われ、学習の進行を促進します。
KL情報量(Kullback-Leiblerダイバージェンス)
KL情報量は、2つの確率分布の間の「違い」を測る尺度です。交差エントロピーと似ていますが、こちらはある確率分布を別の確率分布で近似する際の「情報の損失」を測ります。
数式で表すと以下のようになります。
ここで、
P は真の確率分布、
Q は近似したい確率分布です。この値が0に近いほど、2つの分布は似ていると言えます。
交差エントロピーとKL情報量の違い
交差エントロピー: 真の分布 P とモデルの分布 Q の間の違いを直接測ります。
KL情報量: 真の分布 P をモデルの分布 Q で近似する際の情報の損失を測ります。
実際には、KL情報量は交差エントロピーとエントロピー(真の分布の自己情報量)の差として表現されます。
ここで、H(P) は真の分布 P のエントロピーで、データ自体の不確実性を表します。
ベイズ推定
ベイズ推定は、統計的な推定の一手法で、確率的な不確実性を取り入れた推定方法です。ベイズ推定では、事前の知識(事前分布)と観測データを組み合わせて、パラメータの確率分布(事後分布)を推定します。
ベイズ推定の基本的な考え方は以下の3つのステップからなります。
事前分布の設定: パラメータに対する事前の信念や知識を確率分布で表します。
尤度関数の計算: 観測データが与えられたときのパラメータの尤もらしさ(尤度)を計算します。
事後分布の計算: 事前分布と尤度関数を組み合わせて、パラメータの新しい確率分布(事後分布)を計算します。これが最終的な推定結果です。