kodelifeを使って旭日旗を描いてみます
円を描く
float drawCircle(vec2 uv, vec2 pos, float radius){
float check = 1.f - step(radius,length(uv - pos));
return check;
}
この関数は与えられた座標と円の中心の座標の距離が半径よりも小さい場合1.0を、そうでない場合は0.0を返します。
step(radius,length(uv - pos));
この部分で二点間を結ぶベクトルのノルム(長さ)がstep関数によって 1.0 もしくは 0.0の値に変換されます。
実際に使用した際のコードが以下です。
float drawCircle(vec2 uv, vec2 pos, float radius){
float check = 1.f - step(radius,length(uv - pos));
return check;
}
void main(void)
{
vec2 uv = -1. + 2. * inData.v_texcoord;
vec4 lastCol = vec4(0.0,0.0,0.0,1.0);
vec2 pos = vec2(0.0,0.0);
float circle = drawCircle( uv, pos, 0.3);
lastCol = vec4(1.0,0.0,0.0,1.0) * circle;
fragColor = lastCol;
}
drawCircle関数から返ってきた値とvec4(1.0,0.0,0.0,1.0)の積をとって出力すると
赤色の円が描画されました。
放射模様を描く
先ほど作成したdrawCircleを用いて旭日旗の放射模様も描画してみます。
main文を少し変えてあげて
void main(void)
{
vec2 uv = -1. + 2. * inData.v_texcoord;
vec4 lastCol = vec4(0.0,0.0,0.0,1.0);
vec2 pos = vec2(0.0,0.0);
vec2 centorVect = uv - pos;
float rad = atan(centorVect.y/centorVect.x);
float radiation = drawCircle(uv,pos,cos( rad * 12 ));
float circle = drawCircle(uv, pos, 0.3);
vec4 sun = vec4(clamp(circle + radiation, 0,1), 0.0, 0.0, 0.0);
lastCol = vec4( 1.0, 0.0, 0.0, 1.0) * sun;
fragColor = lastCol;
}
出力結果がこちらです。
要点だけ解説していきます。
atanを用いた角度の算出
vec2 centorVect = uv - pos;
float rad = atan(centorVect.y/centorVect.x);
centorVectが円の中心から各uv座標までのベクトルです。
このベクトルとタンジェントの逆関数atanを用いて円の中心を基準としたuv座標の角度を求めています。
atan関数について簡単に説明すると
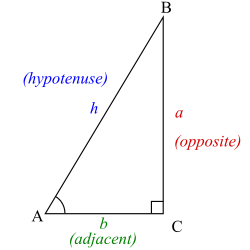
(画像はwikipediaから引用しています。)
上図の直角三角形において∠A = θ に対してtan(θ)は
tan(θ) = a/b
と定義されています。これに対し、tan(θ)の逆関数は
arctan(a/b) = θ \quad(- \pi/2 < θ < \pi/2)
です。
arctanを用いれば、aとbが求められれば直角三角形のなす角∠Aを求めることができます。
ちなみにglslのatanは値域が
(- \pi < θ < \pi)
の範囲で返ってきます。aやbが負数の時もカバーしています。便利!
放射模様
float radiation = drawCircle(uv,pos,cos( rad * 12 ));
ここで放射模様radiationを求めています。
この行が示す内容は 与えられた座標と円の中心の座標の距離がcos( rad * 12 )よりも小さい場合1.0を、そうでない場合は0.0を返します。
少し分かりづらいので図を使って補足すると
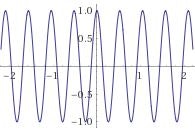
**cos( rad * 12 )**はcos(rad)の周期が1/12になった、上図のような波形をしています。
つまり、半径の閾値を波形にすることで放射模様を描いています。
放射模様をシャープに
void main(void)
{
vec2 uv = -1. + 2. * inData.v_texcoord;
vec4 lastCol = vec4(0.0,0.0,0.0,1.0);
vec2 pos = vec2(0.0,0.0);
vec2 centorVect = uv - pos;
float rad = atan(centorVect.y/centorVect.x);
float radiation = drawCircle(uv,pos,ceil(cos( rad * 12 )));
float circle = drawCircle(uv, pos, 0.3);
vec4 sun = vec4(clamp(circle + radiation, 0,1), 0.0, 0.0, 0.0);
lastCol = vec4( 1.0, 0.0, 0.0, 1.0) * sun;
fragColor = lastCol;
}
書き換えたのはこの部分です。
float radiation = drawCircle(uv,pos,ceil(cos( rad * 12 )));
ceil(x)はx以上の最小の整数を返す関数です。
cos(θ)の値域は
- 1 \leqq cos(θ) \leqq 1
なのでceil(cos(θ))は
ceil(cos(θ)) = 0.0 \quad (-1.0 < cos(θ) \leqq 0.0 ) \\
ceil(cos(θ)) = 1.0 \quad (0.0 < cos(θ) \leqq 1.0 )
になります。
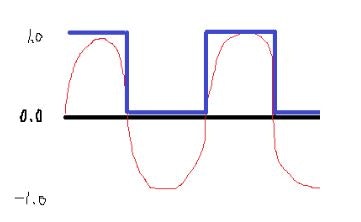
変換前が赤線で変換後が青線です。(汚い図でごめんなさい)
完成
あとは適当に色を変えたりuvを調整したりして完成です。
# version 150
uniform float time;
uniform vec2 resolution;
uniform vec2 mouse;
uniform vec3 spectrum;
uniform sampler2D texture0;
uniform sampler2D texture1;
uniform sampler2D texture2;
uniform sampler2D texture3;
uniform sampler2D prevFrame;
uniform sampler2D prevPass;
in VertexData
{
vec4 v_position;
vec3 v_normal;
vec2 v_texcoord;
} inData;
out vec4 fragColor;
float drawCircle(vec2 uv, vec2 pos, float width){
float check = 1.f - step(width,length(uv - pos));
return check;
}
void main(void)
{
vec2 uv = gl_FragCoord.xy / min(resolution.x,resolution.y) - vec2(max(resolution.x,resolution.y)/min(resolution.x,resolution.y)*0.5,0.5);
uv += vec2(0.16,0.0);
vec4 lastCol = vec4(0.0,0.0,0.0,1.0);
float voice = length(spectrum);
float l = 0.0;
vec2 pos_offset = vec2(-0.0,0.0);
vec2 pos = vec2(l*cos(time),l*sin(time))+pos_offset;
vec2 centVec = uv-pos;
float rad = atan(centVec.y/centVec.x);
float radiation = drawCircle(uv,pos,0.0+voice*10.0*ceil(cos(rad*12+ time*10)));
float circle = drawCircle(uv,pos,0.2);
vec4 sun = vec4(clamp(radiation+circle,0,1),0.0,0.0,0.0);
lastCol += sun.r*vec4(0.97,0.0,0.12,0.0);
lastCol += (1.f-sun.r)*vec4(1.0,0.988,0.87,0.0);
fragColor = lastCol;
}