Swiftコンパイラの構造と基盤テクニック

はじめに

Swiftのソースコードが公開されてから1週間以上が経ちましたが、意外にもまだSwiftコンパイラの構造を解説した日本語記事が少ないので、書いてみることにしました。
SwiftコンパイラはC++で書かれていますが、適切なモジュール化とコーディングスタイルの統一により、とても読みやすいものになっています。
ざっくりとしか解説しませんのでコミッターになれるほど詳細な仕様まではつかめませんが、今後Swiftの仕様がわからなくてソースコードを参照するときの参考や、そもそもコンパイラの構造自体に興味を持っている方の助けになれればと思います。

自分自身Swiftのコミッターというわけではなく、単に少しコンパイラについて学んだことがあるSwift好きという程度ですので、間違っている箇所などあればどしどしご指摘ください。

注意事項

この記事で対象としているソースコードのリビジョンは公開時のもの(8d9ef80)です。公開以降もApple社内外問わずたくさんの方がコミットを続けており、一部の構造や解釈が現在の最新版と異なっている可能性がありますので、注意してください。

apple/swiftレポジトリのディレクトリ構成

公開時のapple/swiftレポジトリのルートディレクトリには以下の様なサブディレクトリが作られています。

swift
├── apinotes
├── benchmark
├── bindings
├── cmake
├── docs
├── include
├── lib
├── stdlib
├── test
├── tools
├── unittests
├── utils
├── validation-test
└── www

今回の記事で触れる内容が実装されているファイルはincludeおよびlib内にあります。これらは、各コードのヘッダファイルと実装の中身が入っているディレクトリであり、Swiftコンパイラを構成するファイルの集まりとなっています。
その他のディレクトリについては各ディレクトリのREADMEに書かれている内容などから目的を知ることができますので説明は割愛しますが、docs内にはSwiftコンパイラの設計に関するドキュメントが置かれていますので、一度目を通しておくとコードの理解の助けになります。

Swiftコンパイラの構成

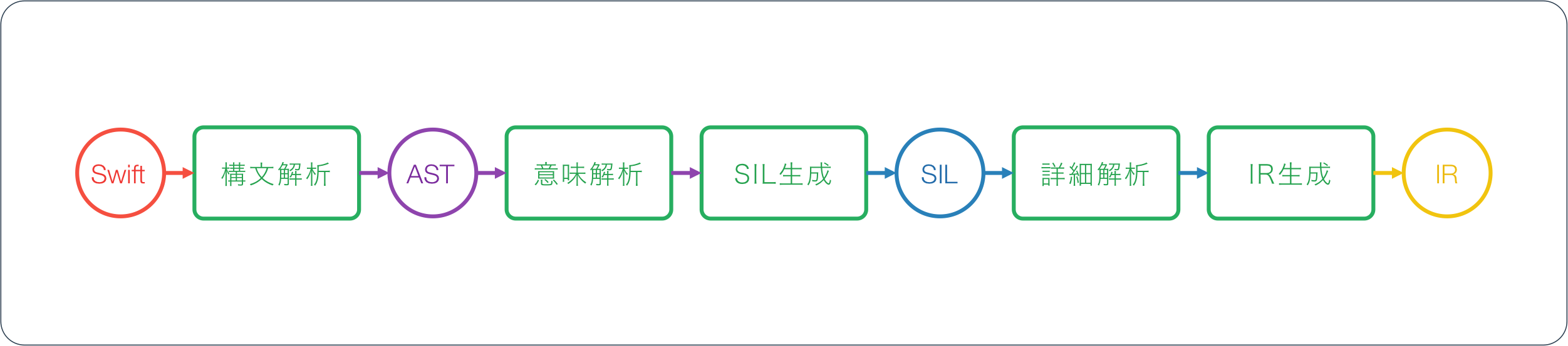
Swiftコンパイラは一般的なコンパイラの「構文解析→意味解析→コード生成」という流れの中にSIL(Swift Intermediate Language)という解析用の中間表現を挟むことでAST(Abstruct Syntax Tree)とコード生成の役割を減らし、全体の見通しをすっきりさせている点が特徴的です。

※ 上図はJoe GroffとChris LattnerによるSwift Intermediate Language (PDFスライド)内の図を日本語に直したものです

まずは各ステップの概要を解説していきます。

構文解析

構文解析ではソースコードの文字列を読み進めてトークンに分け(字句解析)、出来る限り変数などの参照を解決した上でASTにまとめ上げます。
構文解析にはいくつかの手法がありますが、Swiftコンパイラは任意個のトークンを先読みする再帰下降構文解析(LL(k))を採用しており、DSLは使用せずにC++で直接各構文を表す関数を記述してこれを再帰的に呼び出しながらASTを構築していきます。
LL(k)方式には実際の解析処理が人が構文定義を読むのとほぼ同じ流れで進んでいくためにとても読みやすく、意味単位ごとに解析関数がまとまっているためにユニットテストを書きやすい、というメリットがあります。
この構文解析の手法については後でより詳しく解説します。

構文解析はinclude/swift/Parseおよびlib/Parse以下のファイルで実装されています。
また、構文解析によって生成されるASTはinclude/swift/ASTおよびlib/AST以下のファイルで実装されています。

意味解析

意味解析では構文解析で解決できなかった変数などの参照の解決、メンバー呼び出しの解決、型推論と型検査を行います。
GCCなどのレガシーなコンパイラではここに構文のチェックなども含められ、ASTを変形させながらあれこれやっていたのですが、Swiftでは実行フローに関する詳細なエラー検出などはSIL生成後に行います。
型推論ではTaPLでもおなじみのHindleyとMilnerによるアルゴリズムの拡張版を用いています。
このアルゴリズムではAST内の型を持ちうる各ノードに対して同じ型となる部分を制約として列挙し、その制約関係から方程式を解くように型を決定します。
後で型推論の理論についてもう少し詳しく解説します。

意味解析はinclude/swift/Semaおよびlib/Sema以下のファイルで実装されています。

SIL生成

Swiftコンパイラでは意味解析後にいきなりLLVMレベルの構文まで落とすのではなく、まず独自の中間表現であるSILを生成します。
SILの生成はコンパイラの定石通りVisitorパターンを用いてASTを走査して行われます。
SILはLLVM-IRのようにModule、Function、BasicBlockといった構造を持ちますが、ループやError Handlingの情報は残されたままであったり、仮想関数テーブルや型情報を構造化された形のまま保持していたりと、Swiftの意味を維持して強力なエラー検知とメモリ管理、高レベルでの最適化などを行える用に設計されています。

SIL生成はlib/SILGen以下のファイルで実装されています。
また、生成されるSILはinclude/swift/SILおよびlib/SIL以下のファイルで実装されています。

詳細解析

詳細解析では、生成したSILからコールグラフやクラス階層などを抽出し、詳細なエラーの検出やARC(Automatic Reference Counting)方式によるメモリ管理、高レベルでの最適化などを実際に適用してSILコードの書き換えやIR生成に用いる情報の追加などを行います。
SILにもLLVMのようなPassの概念が導入されているため各解析や最適化はうまくモジュール化されており、今後もコンパイラの性能を向上する様々な解析が追加されていくことが予想できます。

詳細解析はinclude/swift/SILAnalysis、include/swift/SILPassesおよびlib/SILAnalysis、lib/SILPasses以下のファイルで実装されています。

IR生成

すべての解析の完了後にはいよいよLLVM-IRを生成します。
LLVMはコンパイラのフロントエンド(ここまでに概説した各解析ステップ)とバックエンド(各プラットフォームの機械語への翻訳と最適化のステップ)を分離し効率化するための中間言語(LLVM-IR)とその生成APIライブラリおよび各種関連ツールの集まりです。
AppleはかねてよりLLVMおよびLLVMで実装されたCファミリのコンパイラClangの開発に大きく関わっており、SwiftのIR生成を行うにあたってLLVM自体にも拡張を施しています。
コンパイラの中心的な開発言語としてC++を選択したのも、このLLVMの最新のAPIがC++で提供されているということが大きな要因となっています。

IR生成では、ここまでで構成したSILからLLVMのAPIを利用してLLVM-IRを生成していっているのですが、この付近はまだあまり読み込めておらず具体的にどの情報からどういったコードを生成しているのかまでは理解できていないので、この程度の説明に抑えておきます。

IR生成はlib/IRGen以下のファイルで実装されています。

Swiftコンパイラの基盤テクニック

ここからは、Swiftコンパイラで使われているテクニックの詳細を解説します。

構文解析

LL方式とLALR方式

近年のコンパイラでは構文解析にLALR(1)またはLL(k)と呼ばれる手法がよく用いられています。
LALRは先読みありのボトムアップ構文解析、LLはトップダウン構文解析を表しており、( )内の値は先読みするトークンの数を示しています。

ボトムアップ構文解析では現在の状態と読んでいるトークンから解析器の次の状態を決定する遷移関数を用いて構文の解析を進め、その副作用としてASTを構築していく手法です。
そのため、ボトムアップ構文解析ではBNF記法よりも更に抽象化された状態遷移関数を作っておく必要があり、これを人の手で考えて構成するのは困難なため、通常ではパーサジェネレータと呼ばれる別のソフトウェアを用いてBNFなどの別言語から構文解析プログラムを自動生成します。
LALR方式のパーサジェネレータにはyaccなどのソフトがよく使用されます。

一方トップダウン構文解析で最もよく用いられる形式である再帰下降構文解析では、構文ごとにそれを解析する関数を用意し、より上位の構文から呼び出す形を取ります。
そのため、再帰下降構文解析のプログラムはそのまま書き下されることが多く、それが結果として先読みの数の柔軟性や解析器の自由度の向上といったメリットをもたらすこともあります。
トップダウン解析にもANTLRやBoost.Spiritのようなパーサジェネレータはありますが、トップダウン構文解析器の自動生成は容易では無いためにLALRと比べると効率が悪く、また柔軟性などのメリットを享受できなくなってしまうため、あまり大規模なコンパイラには使用されていません。

Swiftでの複雑な構文への対処

SwiftではLL(k)方式を用いているため、かなり先読みが必要な構文でも効率よく処理できるようになっています。
例として、For文の解析がどのように行われているかを見てみましょう。

for i; ; {}

for i in xs {}

これら2つのFor文はlib/Parse/ParseStmt.cpp内のparseStmtFor関数で解析されていますが、それがForIn型の構文なのかC言語型の構文なのかは続く;かinを見つけるまで判断できません。
これをどうやって解析しているかというと、まさにその直感のまま、単にコードに書き下すことで実現しています。

// 現在のトークンが変数名か'_'で、次のトークンが','か'in'であるか、現在のトークンが'in'であるなら、ForIn型として解析する
if ((Tok.isIdentifierOrUnderscore() && peekToken().isAny(tok::colon, tok::kw_in)) || Tok.is(tok::kw_in))
  return parseStmtForEach(ForLoc, LabelInfo);

bool isCStyleFor = false;
{
  Parser::BacktrackingScope Backtrack(*this);

  consumeIf(tok::l_paren);

  // ファイルの終端か'in'か';'か'{'に当たるまで読み進める
  while (Tok.isNot(tok::eof, tok::kw_in, tok::semi, tok::l_brace))
    skipSingle();

  // ';'か'{'かファイルの終端にあたった場合はC言語型として解析する
  isCStyleFor = Tok.isAny(tok::semi, tok::l_brace, tok::eof);
}

if (isCStyleFor)
  return parseStmtForCStyle(ForLoc, LabelInfo);

// それ以外の場合はForIn型として解析する
return parseStmtForEach(ForLoc, LabelInfo);

※ 上記コードは実際のコードからコメント部分を省略し、独自のコメントを追加したものです。

どちらの形式のFor文なのかを判断する箇所はinか;かファイル終端に当たるまでの無限ループになっているので、下手を打つと長時間のループになってしまいそうな不安を覚えますが、現実的には正しい構文であれば;かinはせいぜい2~3トークンのうちに出てきますし、ファイル終端まで読まれる場合はエラーとなる場合だけなので、現実的には全く問題がないことがすぐに分かります。

このように、必要な数だけの先読みで読みやすい形式で書き下せるのがLL(k)方式のメリットです。
恐らくAppleでもその柔軟性と効率、メンテナンス性などのトレードオフを考慮した結果、LL(k)方式を選ぶこととなったのではないでしょうか。

型推論

Swiftで使用されているHindleyとMilnerによるアルゴリズムは関数型言語の型推論で最も一般的に使われているものですが、Swiftではこれをさらにメンバー呼び出しや関数のオーバーロード、総称型なども対応できるように拡張して使用しています。

このアルゴリズムでは、まずコード中の型を持ちうる箇所の内、同じ型となる箇所を列挙した集合(制約集合)を作ます。この際、型が明示されていない項の型は変数で表現します。
その後、制約集合の各要素に以下のルールの内あてはまるものを適用し、鶴亀算のように変数となっていた型を決定します。
(このルールの手続きは型システム入門の22.4節に書かれている単一化アルゴリズムを説明の都合から改変したものであり、実際のSwiftコンパイラにおける実装とは異なります)

(ルール1)
　どちらも変数を含まない型である場合はそれらの型が同じか継承関係にあることを確認する。そうなってればその要素を制約集合から削除し、次の要素に進む。そうなっていなければ、エラーとなる
(ルール2)
　左辺が変数である場合は、結果のリストと制約集合中のその変数を全て右辺の型で置き換え、この要素を結果のリストに加え、次の要素に進む
(ルール3)
　右辺が変数である場合は、結果のリストと制約集合中のその変数を全て左辺の型で置き換え、この要素を結果のリストに加え、次の要素に進む
(ルール4)
　右辺と左辺がどちらも関数である場合は、その引数の型同士、戻り値の型同士で新たな要素を作り、制約集合の末尾に加えて次の要素に進む
(ルール5)
　どのルールにも当てはまらなかった場合は、エラーとなる

型推論アルゴリズムの例

言葉だけで書いてもわかりづらいので、簡単なコードでこのアルゴリズムの流れを見て行きましょう。
なお、ここでは関数の引数が実際にはタプル型であるとか、数値リテラルがIntegerLiteralConvertibleを継承したどのクラスとしても判断できる、といった実装の詳細は無視します。

let a = 100

func f(x: Int) -> Int {
    return x + 10
}

print(f(a))

このコードから明示的に型が分かるもののリストは以下です。

• 100はInt型
• fはInt -> Int型
• xはInt型
• +は(Int, Int) -> Int型
• 10はInt型
• printはAny -> ()型

残りの型がわからない項に変数を振ります

• aはT1型とする
• x + 10はT2型とする
• f(a)はT3型とする

ここから、制約集合は以下のようになります。

• T1 == Int
  • aと100は代入関係にある
• (Int, Int) -> T2 == (Int, Int) -> Int
  • xと10を引数にとってx + 10となる関数が+
• Int -> T2 == Int -> Int
  • xを引数にとってx + 10を返す関数がf
• T1 -> T3 == Int -> Int
  • aを引数にとってf(a)となる関数がf
• T3 -> () == Any -> ()
  • f(a)を引数にとって()となる関数がprint

では、上述のアルゴリズムを使って本当に方が導き出せるか確認してみましょう。

1つ目の要素: T1 == Int

(ルール2)により、このルールを結果のリストに加え、制約集合中のT1を全てIntに置き換えます。

結果のリスト
T1 == Int

制約集合
(Int, Int) -> T2 == (Int, Int) -> Int
Int -> T2 == Int -> Int
Int -> T3 == Int -> Int
T3 -> () == Any -> ()

2つ目の要素: (Int, Int) -> T2 == (Int, Int) -> Int

(ルール4)により、型を分解して新しい要素を制約集合に加えます。

結果のリスト
T1 == Int

制約集合
Int -> T2 == Int -> Int
Int -> T3 == Int -> Int
T3 -> () == Any -> ()
(Int, Int) == (Int, Int)
T2 == Int

3~5つ目の要素

これらも全て(ルール4)が適用できるので、型を分解します。

結果のリスト
T1 == Int

制約集合
(Int, Int) == (Int, Int)
T2 == Int
Int == Int
T2 == Int
Int == Int
T3 == Int
T3 == Any
() == ()

6つ目の要素: (Int, Int) == (Int, Int)

(ルール1)により型が等しいので、次に進みます。

結果のリスト
T1 == Int

制約集合
T2 == Int
Int == Int
T2 == Int
Int == Int
T3 == Int
T3 == Any
() == ()

7つ目の要素: T2 == Int

(ルール2)により、このルールを結果のリストに加え、制約集合中のT2を全てIntに置き換えます。

結果のリスト
T1 == Int
T2 == Int

制約集合
Int == Int
Int == Int
Int == Int
T3 == Int
T3 == Any
() == ()

8~10個目の要素

(ルール1)により型が等しいので、次に進みます。

結果のリスト
T1 == Int
T2 == Int

制約集合
T3 == Int
T3 == Any
() == ()

11個目の要素: T3 == Int

(ルール2)により、このルールを結果のリストに加え、制約集合中のT3を全てIntに置き換えます。

結果のリスト
T1 == Int
T2 == Int
T3 == Int

制約集合
Int == Any
() == ()

12個目の要素: Int == Any

(ルール1)により型が継承関係にあるので、次に進みます。

結果のリスト
T1 == Int
T2 == Int
T3 == Int

制約集合
() == ()

13個目の要素: () == ()

(ルール1)により型が等しいので、次に進みます。

結果のリスト
T1 == Int
T2 == Int
T3 == Int

制約集合
なし

かなり冗長な箇所がありましたが、結果として明示されている型は全て正しく型付けされていることを確認でき、明示されていなかった型は推論して決定することができました。

Swiftでの型推論アルゴリズムの実装

Swiftでは制約集合を単に「型が等しい」というだけでなく、「メンバ呼び出しの結果の型が等しい」、「左辺が右辺の子クラスである」、「左辺が右辺のプロトコルである」というようなより具体的な制約の集合とした上でそれぞれのためのルールを追加し、このアルゴリズムを多様なSwiftの仕様でも使えるように拡張しています。
これらの詳しい説明についてはdocs/TypeChecker.rstにかかれていますので、一度目を通すとよりSwift独自の拡張について知ることができるかと思います。

おわりに

というわけで、この記事ではSwiftのソースコードの外観と構文解析・型推論の理論について眺めました。
なかなかコンパイラ関係以外では役立たない知識ではありますが、こうしたコンパイラの基礎の部分をなんとなくでも分かった気でいると、今後のSwiftの変化を素直に受け入れられたり、逆によくない変化を敏感に感じ取ったりすることができ、少しでもSwiftの頻繁な仕様変更に振り回されることが少なくなるのではないでしょうか。

また、最後にちょこっとだけ宣伝ですが、実は私は諸事情により今年のはじめくらいからオープンソースでTreeSwiftというSwiftで記述したSwiftコンパイラを実装しています。
まだまだできていない部分が多くお恥ずかしい限りですが、もしC++のコードは少し抵抗があるけどSwiftのコンパイラのコードを追ってみたいという方がいましたら、こちらの実装でもLL(k)方式の構文解析とHindleyとMilnerによる型推論アルゴリズムを採用していますので、参考程度に覗いてみてください。

長ったらしい駄文にお付き合い下さり、ありがとうございました。