『深層学習』を読んだので理解を深めるためにNNを実装してみたくなった。自分は機械学習に興味がある程度の素人、勉強不足だけど実践を通じていろいろ学びたい。 あとディープラーニングで一発当てたい
実用として使うならChainerみたいなちゃんとしたライブラリがあるので、飽くまで自分の学習用にほどほどテキトーに作る。
使う言語はClojure。自分でもよく分かっていないモノを試行錯誤しながらプログラミングするにはREPLがある言語が便利だし、自分はClojureに慣れてるので。
二値分類まではなんとなーく出来たのでそれまでの記録を書いてみたい。
ソース:https://github.com/deltam/neuro
NNの表現
(def nn {:nodes [3 2 1]
:weights [
[[0.0 0.0]
[0.0 0.0]
[0.0 0.0]]
[[0.0]
[0.0]]
]
:func :logistic})
こんな感じで層ごとのノード数や重み行列を表現できたらいいなーと思って実装した。
(バイアス項は、入力xのひとつを1に固定して重みで表現する方法にした)
こんな感じで使える。
user> (require '[neuro.network :as nw])
nil
user> (clojure.pprint/pprint (nw/gen-nn 0.1 3 2 1))
{:nodes [3 2 1],
:weights [[[0.1 0.1] [0.1 0.1] [0.1 0.1]] [[0.1] [0.1]]],
:func :logistic}
nil
;; 初期値をランダムにする
user> (clojure.pprint/pprint (nw/gen-nn :rand 3 2 1))
{:nodes [3 2 1],
:weights
[[[0.20976756886633208 0.825965871887821]
[0.17221793768785243 0.5874273817862956]
[0.7512804067674601 0.5710403484148672]]
[[0.5800248845020607] [0.752509948590651]]],
:func :logistic}
;; 3層以上も定義できる
user> (clojure.pprint/pprint (nw/gen-nn 0.1 3 3 2 1))
{:nodes [3 3 2 1],
:weights
[[[0.1 0.1 0.1] [0.1 0.1 0.1] [0.1 0.1 0.1]]
[[0.1 0.1] [0.1 0.1] [0.1 0.1]]
[[0.1] [0.1]]],
:func :logistic}
nil
NNの計算
入力xのvectorを与えてvectorが出力されるように作った。
user> (require '[neuro.core :as core])
nil
user> (def nn (nw/gen-nn :rand 3 2 1))
# 'user/nn
user> (core/nn-calc nn [0.2 0.3 1])
[0.5733569426792443]
NNの学習
NNはノード間の重みを調節することで学習を行なう。そのためには学習データと誤差関数が必要になる。
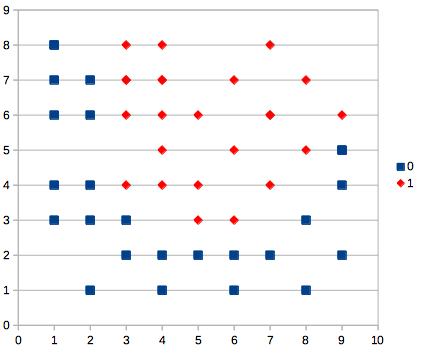
学習データは適当に10x10の領域を分割するようなカタチを想定して、テキトーに用意した。
(def traindata-2class [{:x [2 5 1] :ans [0]}
{:x [3 2 1] :ans [0]}
{:x [4 1 1] :ans [0]}
{:x [8 3 1] :ans [0]}
{:x [1 8 1] :ans [0]}
{:x [9 5 1] :ans [0]}
{:x [5 2 1] :ans [0]}
{:x [4 2 1] :ans [0]}
{:x [3 3 1] :ans [0]}
{:x [2 6 1] :ans [0]}
{:x [1 8 1] :ans [0]}
{:x [9 5 1] :ans [0]}
{:x [1 4 1] :ans [0]}
{:x [2 4 1] :ans [0]}
{:x [1 6 1] :ans [0]}
{:x [2 3 1] :ans [0]}
{:x [6 1 1] :ans [0]}
{:x [9 4 1] :ans [0]}
{:x [7 2 1] :ans [0]}
{:x [6 2 1] :ans [0]}
{:x [8 1 1] :ans [0]}
{:x [9 2 1] :ans [0]}
{:x [2 1 1] :ans [0]}
{:x [2 7 1] :ans [0]}
{:x [1 3 1] :ans [0]}
{:x [1 7 1] :ans [0]}
{:x [3 7 1] :ans [1]}
{:x [4 4 1] :ans [1]}
{:x [7 6 1] :ans [1]}
{:x [3 7 1] :ans [1]}
{:x [4 8 1] :ans [1]}
{:x [7 8 1] :ans [1]}
{:x [7 6 1] :ans [1]}
{:x [4 5 1] :ans [1]}
{:x [4 7 1] :ans [1]}
{:x [8 5 1] :ans [1]}
{:x [6 3 1] :ans [1]}
{:x [4 7 1] :ans [1]}
{:x [9 6 1] :ans [1]}
{:x [7 4 1] :ans [1]}
{:x [3 8 1] :ans [1]}
{:x [3 4 1] :ans [1]}
{:x [5 6 1] :ans [1]}
{:x [6 5 1] :ans [1]}
{:x [5 4 1] :ans [1]}
{:x [5 3 1] :ans [1]}
{:x [4 6 1] :ans [1]}
{:x [8 7 1] :ans [1]}
{:x [3 6 1] :ans [1]}
{:x [6 7 1] :ans [1]}
])
誤差関数は『深層学習』2.4.3 二値分類に載っていた誤差関数を使う。
(defn diff-fn-2class
"2値分類の誤差関数 nn の出力層は1ニューロン"
[nn dataset]
(let [samples (count dataset)
diff-sum (apply +
(for [{x :x, [d] :ans} dataset
:let [[y] (core/nn-calc nn x)]]
(+ (* d (Math/log y))
(* (- 1.0 d) (Math/log (- 1.0 y))))))]
(/ (* -1 diff-sum) samples)))
本に載ってるのと違いサンプル数で割っているのは、学習データの数が違うときでも誤差値を比較しやすくするため。
ランダム重み更新
なんだかここまで作って疲れてきた ![]() 。 学習方法とか数式から読み取ってコーディングするのも面倒な気分になって、 「重みをテキトーに動かして誤差関数が小さくなったらその重みで更新すりゃーいいんじゃないんか」 と横着なことを考えた。
。 学習方法とか数式から読み取ってコーディングするのも面倒な気分になって、 「重みをテキトーに動かして誤差関数が小さくなったらその重みで更新すりゃーいいんじゃないんか」 と横着なことを考えた。
(ns neuro.train
(:require [neuro.core :as core]
[neuro.network :as nw]
[clojure.data.generators :as gr]))
(def ^:dynamic *weight-random-diff* 0.001)
(def ^:dynamic *report-period* 100) ; 更新100回ごとに誤差値レポート
(defn train [init-nn dfn w-updater dataset terminate-f]
(loop [cur-nn init-nn, diff (dfn init-nn dataset) , cnt 0]
(let [next (train-next cur-nn dfn w-updater dataset)
next-diff (dfn next dataset)]
(if (zero? (mod cnt *report-period*))
(println cnt " now diff: " next-diff))
(if (terminate-f diff next-diff)
cur-nn
(recur next, next-diff, (inc cnt))))))
(defn train-next [nn dfn w-updater dataset]
(let [nn1 (w-updater nn dfn dataset)
diff1 (dfn nn1 dataset)
nn2 (w-updater nn dfn dataset)
diff2 (dfn nn2 dataset)]
(cond (<= diff1 diff2) nn1
(> diff1 diff2) nn2)))
;; ランダム更新
(defn- rand-add [x]
(+ x
(gr/rand-nth [*weight-random-diff*
0
(* -1 *weight-random-diff*)])))
(defn weight-randomize
"重みをランダムに更新する"
[nn dfn dataset]
(binding [gr/*rnd* (java.util.Random. (System/currentTimeMillis))]
(nw/map-weights (fn [w l i o] (rand-add w))
nn)))
(Clojure豆知識:短時間でランダム値を複数作りたい場合は clojure.data.generators を使うべし。ふつうにrandを使うと同じ数値になってしまう)
初期重みランダムのNNをデータから学習させてみる。
user> (require '[neuro.train :as tr])
nil
user> (def nn (nw/gen-nn :rand 3 6 1))
# 'user/nn
user> (time (def nn-r
(tr/train nn tr/diff-fn-2class tr/weight-randomize tr/traindata-2class (fn [_ d] (< d 0.2)))
))
0 now diff: 1.8755375627981343
100 now diff: 1.8230800316637328
200 now diff: 1.7709671117257861
300 now diff: 1.7181116335717421
400 now diff: 1.6668682069476832
500 now diff: 1.611435391226951
...
40500 now diff: 0.20469674617156725
40600 now diff: 0.20320516843366657
40700 now diff: 0.2021819619602946
40800 now diff: 0.20122757877052513
40900 now diff: 0.2005773226889801
"Elapsed time: 135231.290044 msecs"
# 'user/nn-r
user> nn-r
{:nodes [3 6 1], :weights [[[-1.6322905386460618 0.8474264426332738 1.5164608145186957 1.006524133735246 -1.3338148714534757 0.41288614157208736] [-0.14701069918606588 0.9856379438786887 0.6137505144406843 0.9185581146529809 2.2206110537993666 0.3038935564489956] [5.024415204130707 1.176886941218098 1.3125489924132216 0.5669286531234229 0.4812070787884914 -1.721984916619937]] [[-5.014729365568847] [-1.3161836903024] [-1.67535089053784] [-1.409897155916921] [5.122658210002135] [2.3911571536050675]]], :func :logistic}
学習の打ち切り条件はテキトーに誤差値0.2未満にしてみた。もうちょっと小さくできるみたい。
分類能力を試してみる。
いろいろ考えたけどグラフにプロットして視覚化するのがいちばん分かりやすい。次のような関数を書いて、10x10のランダムな点を120個ぐらい計算させてみた。
(defn plot-classify
"ランダムな数値を分類させて結果をCSVで出力する"
[nn count]
(binding [gr/*rnd* (java.util.Random. (System/currentTimeMillis))]
(let [samples (for [i (range count)
:let [x1 (int (* 10 (gr/double)))
x2 (int (* 10 (gr/double)))
[v] (core/nn-calc nn [x1 x2 1])
ok (if (< 0.5 v) 1 0)]]
[x1 x2 1 ok v])]
(doseq [[x1 x2 _ ok _] (sort-by #(nth % 4) samples)]
(printf "%d,%d,%d\n" x1 x2 ok)))))
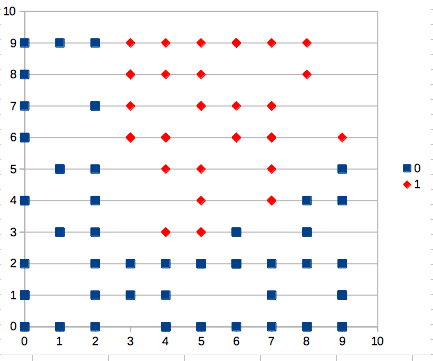
表計算ソフトで散布図にしてみると次のような感じ。
おぉ、なんか結構学習データのグラフと似てるぞ。ランダム重み更新でも学習できるみたいですね。
勾配降下法
ランダム学習が予想外に上手くいってしまったけど、勾配降下法も作ることにする。
難しく考えてたけど、ようはグラフの傾きを見て下向きの方へ重みの値を寄せていく方法なのね。
上のtrain関数では重み更新の処理を引数で渡せるようにしてあるので、勾配降下法で重みを更新する関数だけ定義する(FPバンザイ!)
(def ^:dynamic *weight-inc-val* 0.00001)
(def ^:dynamic *learning-rate* 0.00001)
;; 勾配降下法
(defn- gradient
"nnの微小増分の傾きを返す"
[nn dfn dataset level in out]
(let [w (nw/weight nn level in out)
nn-inc (nw/update-weight nn (+ w *weight-inc-val*) level in out)
y (dfn nn dataset)
y-inc (dfn nn-inc dataset)]
(/ (- y-inc y) *weight-inc-val*)))
(defn- update-by-gradient
"重みを勾配に従って更新した値を返す"
[w nn dfn dataset level in out]
(let [grd (gradient nn dfn dataset level in out)]
(- w (* *learning-rate* grd))))
(defn weight-gradient
"勾配降下法で重みを更新する"
[nn dfn dataset]
(nw/map-weights (fn [w l i o]
(update-by-gradient w nn dfn dataset l i o))
nn))
勾配降下法では勾配を出すために誤差関数の微分が必要だけど、計算が面倒なので微分の定義で出てくる (f(x+h) - f(x)) / h を使って勾配を出した。誤差関数を二重に計算する必要があるからのちのちネックになりそうだなー(意識低い系設計なのでまずは良し)。
ランダム重み更新と同じく打ち切り条件は誤差値0.2未満にしてみた。
user> (def nn (nw/gen-nn :rand 3 6 1))
# 'user/nn
user> (time (def nn-g
(tr/train nn tr/diff-fn-2class tr/weight-gradient tr/traindata-2class (fn [_ d] (< d 0.2)))
))
0 now diff: 1.8625548058140031
100 now diff: 0.9159858572606195
200 now diff: 0.7161057750427706
300 now diff: 0.6990925986483871
...
35000 now diff: 0.20315615388662528
35100 now diff: 0.20260568927896344
35200 now diff: 0.20205889456320478
35300 now diff: 0.20151573743521456
35400 now diff: 0.20097618588659338
35500 now diff: 0.200440208191568
"Elapsed time: 3723826.649624 msecs"
# 'user/nn-g
user> nn-g
{:nodes [3 6 1], :weights [[[0.9476824494425211 0.7742720581326019 1.548718284318479 1.0507296802976875 -0.8104515255968177 -0.6706549275076373] [1.2801447793603153 1.2030460046783422 0.012586512769285574 1.158871756033361 1.6259846088747263 1.3410827184888816] [0.8501839044170969 1.052285270512655 -4.051173560144101 0.7020271010358694 -1.1310995384148081 -0.892625581728861]] [[-3.5135386389691803] [-2.8458019517840354] [6.684181788934695] [-2.9414483024037072] [3.6869865857248842] [2.539847467590837]]], :func :logistic}
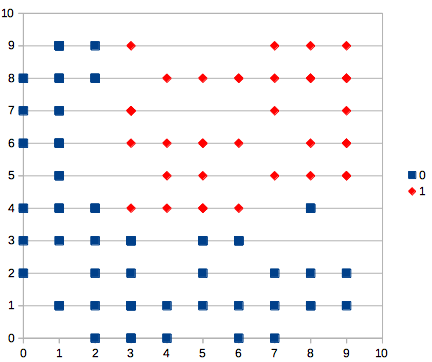
時間掛かった。つぎにランダム学習と同じくプロット。
分類できてるみたいだけど、ランダム重み更新の場合とどう違うのかがわからん。
まとめ
- NNの実験をするためのコードはできた。
- 二値分類はできた(ような気がする)
- ランダム重み更新が上手くいってるのは単純なNNだから?
- 分類器の評価方法は要調査。
- 分類結果は視覚化するとデバッグしやすくて良い
今後
mnistの手書き数字データを読み込むコードを先に書いてしまったので、多クラス分類を精度よくできる程度までは続けたい。