0.なぜ線形代数を学ぶ必要があるのか？
プログラミングの世界では複雑な処理を簡略化するためのタグや関数（繰返し処理など）が多く存在している。
線形代数は、複雑な計算式などを簡略化させるために誕生したもの。
Pythonのような簡略化が重要なプログラミングにおいて、線形代数の仕組みや理論を活用し、シンプル化を実現している。
1.線形代数とは
代数というのはxやyのことであり、その部分にどのような数字が入るかわからないからひとまずxなどを代わりに使おう、という考えの元使用されている。
そしてその代数をさらに簡略化させたものが、線形代数。
2.連立方程式と行列
連立方程式も線形代数の一つ
次のような連立方程式がある
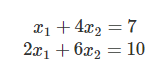
これを数式で解くかわりに、行列を使ってシンプルな形にして解くことが出来る。この連立方程式を行列で表すと以下である。
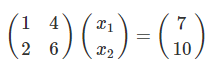
この行列を変形させると、x1とx2が求まる。
3.単位行列と逆行列
単位行列とは、「対角成分が全て1で、それ以外は全て0な正方行列」のこと
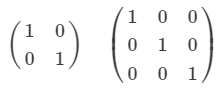
逆行列とは、「元の行列にかけると単位行列になるもの」のこと
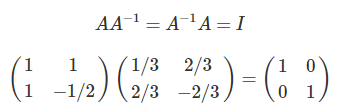
# 4.固有値と固有ベクトル
n次正方行列Aとλに対して、
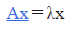
を満たすゼロベクトルでないn次列ベクトル
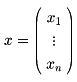
があるとき、λを行列Aの固有値といい、xをAの固有値λに対する固有ベクトルという
5.特異値（分解）
線形代数学における複素数あるいは実数を成分とする行列に対する行列分解の一手法
