E資格合格に向けて 深層学習day1

Section0 ニューラルネットワークとは

ニューラルネットワークは機械学習の1つで、人間の神経回路を真似することで学習を実現しようとするもの。ニューラルネットワークの元祖は、米国の心理学者フランク・ローゼンブラットが1958年に提案した単純パーセプトロンというニューラルネットワーク。このニューラルネットワークを多層にしたものがディープラーニング（深層学習）である。

Section1 入力層~中間層

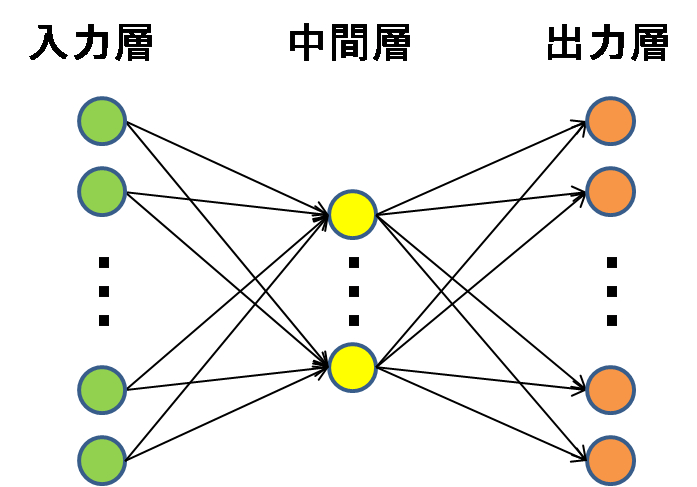
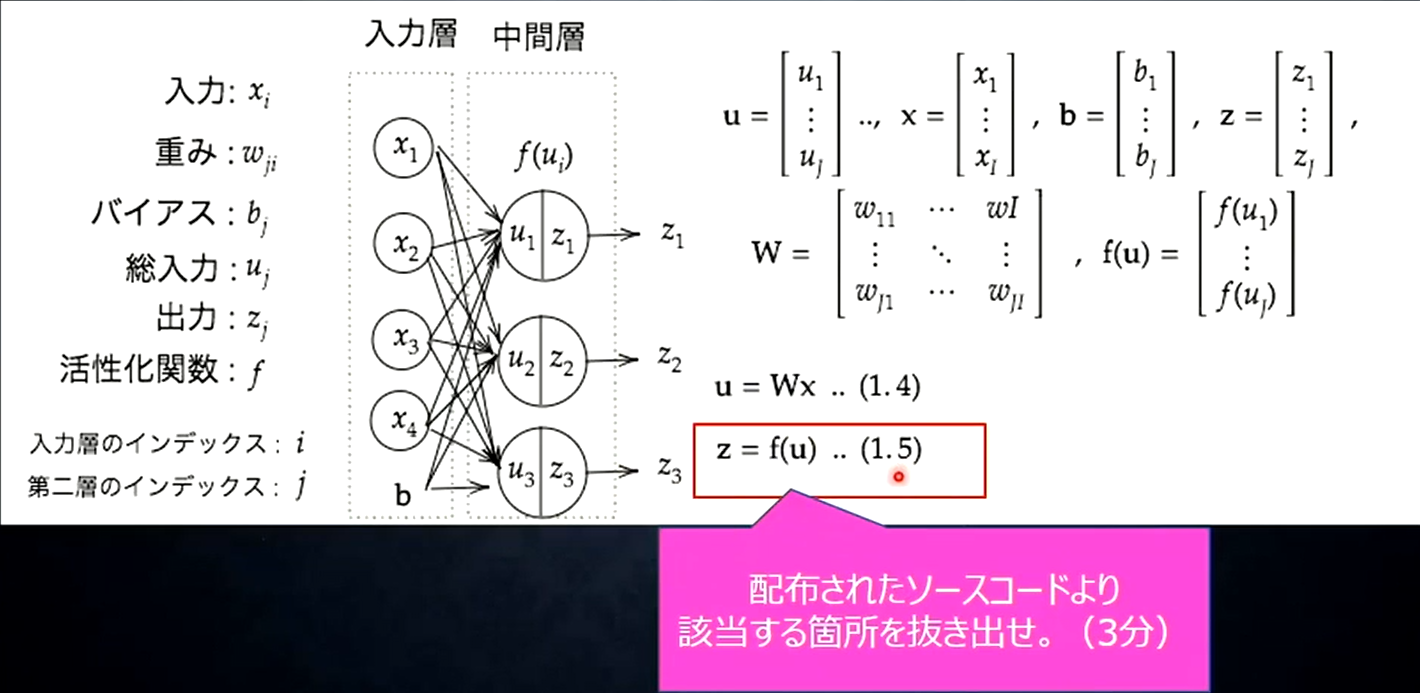
ニューラルネットワークは人間の脳の神経回路が層構造になっている（と考えられている）のにならい、入力を受け取る部分を「入力層」、出力する部分を出力層と表現する。入力層における各ニューロンと、出力層におけるニューロンの間のつながりは重みで表現され、どれだけの電気記号（値）を伝えるかを調整する。そして、出力が0か1の値をとるようにすることで、正例と負例の分類を可能にする。この入力層と出力層だけでは線形分類しかできないが、そこで考えられたのが、更に層を追加するというアプローチ。この入力層と中間層の間に追加された層を中間層（隠れ層）と呼ぶ。隠れ層を追加したことでネットワーク全体の表現力は大きく向上し、多層パーセプトロンでは非線形分類も行う事が出来るようになった。

実装例：入力層と中間層のコーディングイメージ

import numpy as np

# 　シグモイド関数の定義
def sigmoid(a):
    return 1 / (1 + np.exp(-a))

# 一層目（入力層）
x1 = np.array([
    [1],
    [2]
])
# 一層目の重み
w1 = np.array([
    [0.4,0.3],
    [0.7,0.6]
])
a1 = w1.dot(x1)

# 二層目
x2 = sigmoid(a1)
w2 = np.array([
    [0.2,0.3],
    [1.0,0.7]
])
a2 = w2.dot(x2)

# 　出力値と正解値
y = sigmoid(a2)
t = np.array([
    [1],
    [0]
])

【確認テスト】

import numpy as py
# 重み
W = np.array([[0.1], [0.2]])
# バイアス
b = 0.5
# 入力値
x = np.array([2, 3])
# 総入力
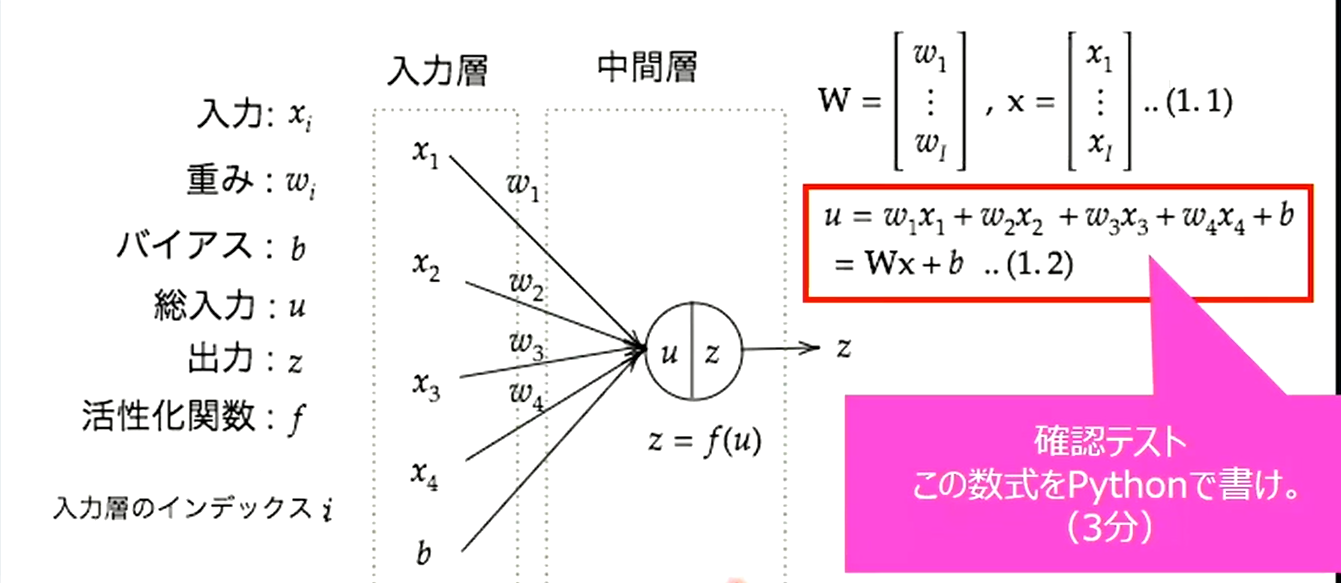
u = np.dot(x, W) + b ←この部分が確認テストの回答

【確認テスト】

def forward(network, x):
    print("##### 順伝播開始 #####")
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    # 1層の総入力
    u1 = np.dot(x, W1) + b1
    
    # 1層の総出力
    z1 = functions.relu(u1)
    
    # 2層の総入力
    u2 = np.dot(z1, W2) + b2
    
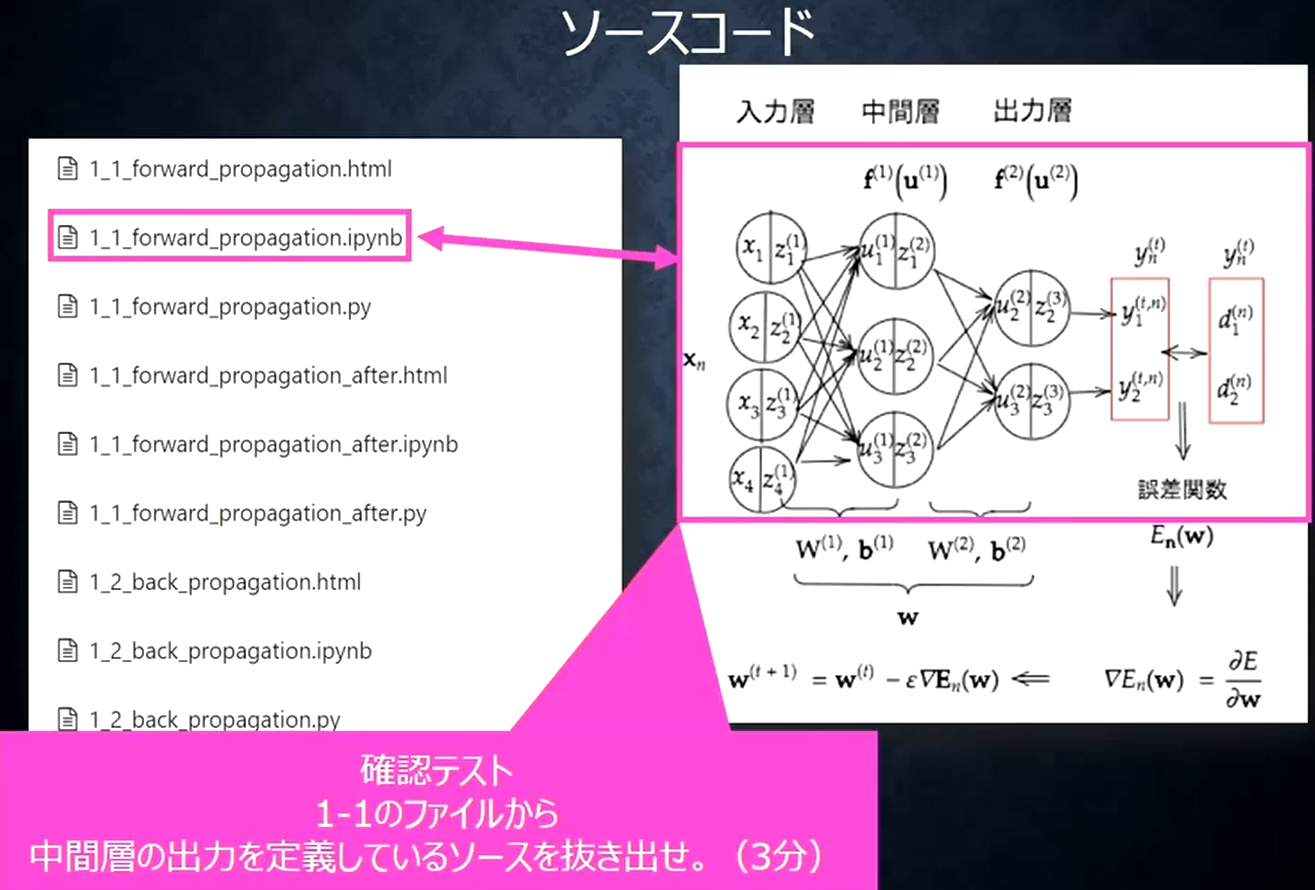
    # 2層の総出力              ←中間層の出力を定義しているソース
    z2 = functions.relu(u2)

    # 出力層の総入力
    u3 = np.dot(z2, W3) + b3
    
    # 出力層の総出力
    y = u3

Section2 活性化関数

層の間をどのように電気信号を伝播させるかを調整する関数を活性化関数という。
活性化関数は中間層と出力層で使われるが、それぞれに位置づけが異なるため以下の通り整理する。

【出力層】
出力を確率で表現する必要がある
・シグモイド関数（ロジスティック関数）
・ソフトマックス関数
・恒等写像

【中間層（隠れ層）】
任意の実数を（非線形に）変換する事が出来る関数であれば、特にどんな関数であろうと問題はない。
・シグモイド関数（ロジスティック関数）
・ReLU関数
・ステップ関数
・tanh(ハイポボリックタンジェント）関数

実装例：シグモイド関数

def sigmoid(a):
    y = 1 / (1 + np.exp(-a))
    return y

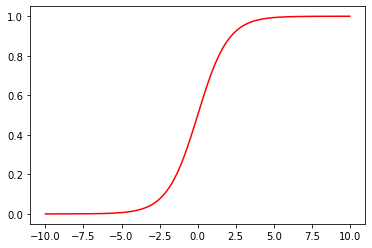
実際に図で表現

import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.01)
y = sigmoid(x)
plt.clf()
plt.plot(x, y, "r")

【確認テスト】

Commonフォルダのfunctionsファイル
# ReLU関数
def relu(x):
    return np.maximum(0, x)

# コード
import numpy as np
from common import functions

def forward(network, x):
    print("##### 順伝播開始 #####")
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    # 1層の総入力
    u1 = np.dot(x, W1) + b1
    
    # 1層の総出力
    z1 = functions.relu(u1)  ←活性化関数が使用されている
    
    # 2層の総入力
    u2 = np.dot(z1, W2) + b2
    
    # 2層の総出力
    z2 = functions.relu(u2)　←活性化関数が使用されている

Section3 出力層（誤差関数）

ニューラルネットワークをはじめとした機械学習の手法が目指しているのは、「モデルの予測値と、実際の値との誤差をなくすこと」。誤差をなくすとは、機械学習は数学的にアプローチをするので、数学的には、先ほどの誤差を誤差関数として定義し、これを最小化することになる。つまり、関数の最小化問題となる。関数の最小化と言えば、微分。それぞれの層の重みで誤差関数を微分した値がゼロになるような重みを求めればいいことになる。ただ、一般的にニューラルネットワークで解こうとするような問題は入力の次元が多次元にわたるので、最適なパラメーターが簡単には求まらないケースがほとんど。そこで、解析的に解を求めていくのではなく、アルゴリズムを用いて最適解を探索する、というアプローチが考えられた。その手法として、勾配降下法が有名である。

実装例：二乗和誤差

def mse(y,t):
    return 0.5 * np.sum((y - t) ** 2 )

【確認テスト】

・2乗する理由
　引き算を行うだけでは、各ラベルでの誤差で正負両方の値が発生し、全体の誤差を正しくあらわすのに都合が悪い。2乗してそれぞれのラベルでの誤差を正の値になるようにするため。
・1/2する理由
　実際にネットワークを学習するときに行う誤差逆伝搬の計算で、誤差関数の微分を用いるが、その際の計算式を簡単にするため。本質的な意味はない。

Section4 勾配降下法

勾配降下法は名前の通り、「勾配に沿って降りていくことで解を探索する」手法。ここでいう勾配とは、微分値に当たる。例えばy=X^2のようなXy平面上で表せる関数では、微分は「接線の傾き」を表すため、微分値が勾配を表しているというのは直観的にも理解しやすい。勾配を坂道に見立て、その坂道に沿って降りていけば、いずれ平らな道に行き着くはず。そして、傾きがゼロ、すなわち微分値がゼロの点なわけなので、まさしく目的の点が得られることになる。
【種類】
・確率的勾配降下法
・ミニバッチ勾配降下法
・オンライン学習
・バッチ学習

実装例：#Section1の実装例の続き

# 入力値,パラメーター,合算値を配列化
X = [x1, x2]
A = [a1, a2]
W = [w1, w2]

# パラメーターが何層あるかのサイズの取得
max_layer = len(X)

# 活性化関数の微分
def f(a):
    return (1 - sigmoid(a)) * sigmoid(a)

# 更新式の公式gの実装
def g(l, j):
    if max_layer == l:
        return(y[j] - t[j]) * f(A[l-1][j])
    else:
        output = 0
        m = A[l-1].shape[0]
        for i in range(m):
            output += g(l+1, i) * W[l][j, i] * f(A[l-1][j])
        return output

# パラメーターwによる誤差関数の微分
def diff(j, k, l):
    return g(l, j) * X[l-1][k]

# パラメーターを100回学習
for _ in range(100):
    for l in range(len(X)):
        for j in range(W[l].shape[0]):
            for k in range(W[l].shape[1]):
                W[l][j, k] = W[l][j, k] - diff(j, k, l+1)
    A[0] = W[0].dot(X[0])
    X[1] = sigmoid(A[0])
    A[1] = W[1].dot(X[1])
    y = sigmoid(A[1])

学習後の回答

【確認テスト】

オンライン学習とは
学習データが入ってくるたびに都度パラメータを更新し、学習を進めて行く方法。一方、バッチ学習では一度にすべての学習データを使ってパラメータ更新を行う。大量のデータの学習をすることが多い深層学習では、バッチ学習のような一度に大量のデータで学習することがハードウェアの容量として難しいため、オンライン学習はよく用いられる。

【確認テスト】

Section5 誤差逆伝播法

層が増えることによって調整すべき重みの数も増えることになるが、予測値と実際の値との誤差をネットワークにフィードバックするアルゴリズムである誤差逆伝播法（backpropagation）が考えられたことで、効率的なネットワーク学習に貢献した。誤差逆伝播法は、算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播させる。最小限の計算で各パラメータでの微分値を解析的に計算する手法。

実装例：Section4の実装例の再掲

# 活性化関数の微分
def f(a):
    return (1 - sigmoid(a)) * sigmoid(a)

# 更新式の公式gの実装
def g(l, j):
    if max_layer == l:
        return(y[j] - t[j]) * f(A[l-1][j])
    else:
        output = 0
        m = A[l-1].shape[0]
        for i in range(m):
            output += g(l+1, i) * W[l][j, i] * f(A[l-1][j])
        return output

【確認テスト】

# 誤差逆伝播
def backward(x, d, z1, y):
    # print("\n##### 誤差逆伝播開始 #####")    

    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y) ←掲載結果を保持するためのコード

delta2は誤差関数の微分値を保持していることになる

【確認テスト】

## 試してみよう
    delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
# W1の勾配
    grad['W1'] = np.dot(x.T, delta1)