LoginSignup
1
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@deepgreenAN

PytorchでRANSAC

Last updated at Posted at 2021-06-30

今回はPytorchで最小二乗法を用いた簡易的なRANSACを実装します．Pytorchではミニバッチを前提とした演算が可能なため，最小二乗フィッティングを用いたRANSACはfor文を用いない実装ができます．しかし計算途中のデータをメモリにのせる必要があるので，場合によっては現実的ではないかもしれません．とはいえループを減らすのに役立つと思います．また，並列に行うためアウトライヤを除くことができません，つまり厳密にはRANSACではないかもしれません．

import numpy as np
import matplotlib.pyplot as plt
import torch

最小二乗法

まずnumpyで実装し，次にpytorchで二つの最小二乗解を並列に求めたいと思います．

numpy

まずは，データの作成を行います．

x = np.arange(0,1,0.01)

a = 2.0
b = 3.0  # このbは距離計算や式におけるcであることに注意

def func(x):
    return a*x+b

y = func(x) + 0.1*np.random.randn(len(x))

fig, ax = plt.subplots()
ax.scatter(x,y)

<matplotlib.collections.PathCollection at 0x1e86ae05f48>

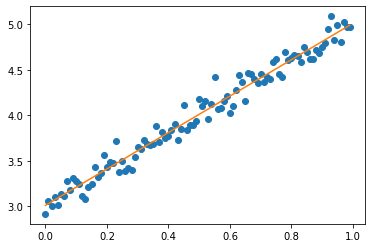
グラフからも分かりますが，$y = ax + c$ $(a=2, c=3)$のデータにノイズが混ざったデータです．
次に，numpyの行列演算で最小二乗解を求めます．

# 計画行列
X = np.stack([x,np.ones(len(x))],axis=1)

# 最小二乗解
inv_XtX = np.linalg.inv(np.dot(X.T,X))
Xty = np.dot(X.T,y)
beta_hat = np.dot(inv_XtX, Xty)
print(beta_hat)

[2.00013207 3.01041776]

最小二乗解をグラフで表示させます．

y_hat = np.dot(X, beta_hat)

fig, ax = plt.subplots()
ax.scatter(x,y)
ax.plot(x,y_hat,color="C1")

[<matplotlib.lines.Line2D at 0x1e86b302f88>]

Pytorch

pytorchではバッチごとに行列の積torch.bmm，逆行列torch.inverse，転置torch.transposeが計算できるので，複数データを並列に最小二乗解を計算できます．

まずは，データの作成を行います．

x_1 = torch.from_numpy(np.arange(0,1,0.01))
x_2 = torch.from_numpy(np.arange(2,3,0.01))

b_x = torch.stack([x_1,x_2],dim=0)

a_1 = 2.0
b_1 = 3.0  # このbは距離計算や式におけるcであることに注意

a_2 = 4.0
b_2 = 5.0  # このbは距離計算や式におけるcであることに注意

def func1(x):
    return a_1*x+b_1

def func2(x):
    return a_2*x+b_2

y_1 = func1(x_1) + 0.1*torch.randn(len(x_1))
y_2 = func2(x_2) + 0.1*torch.randn(len(x_2))

b_y = torch.stack([y_1,y_2],dim=0)

fig, ax = plt.subplots(figsize=(10,10))
ax.scatter(x_1.numpy(), y_1.numpy(), color="C0")
ax.scatter(x_2.numpy(), y_2.numpy(), color="C1")

<matplotlib.collections.PathCollection at 0x1e86b380048>

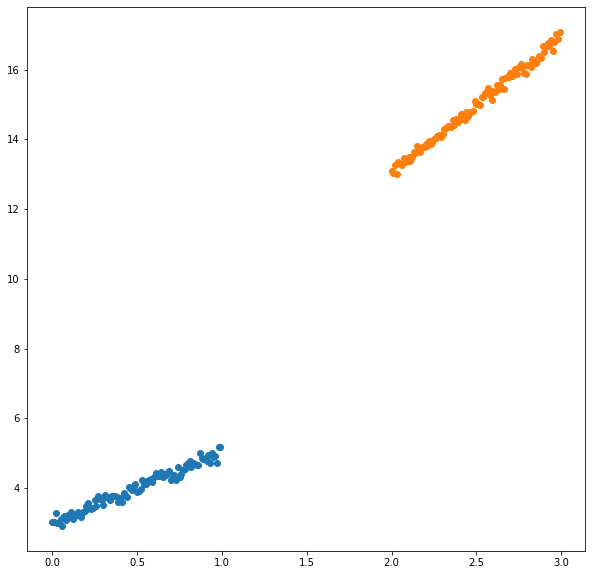
$(a=2, c=3)$と$(a=4, c=5)$にそれぞれノイズがかかったデータです．
Pytorchで並列に最小二乗解を求めます．ここで注意しなければならないのはtorch.bmmは二つのバッチの行列が必要になるので，ベクトルは明示的に行列に変換します．

# 計画行列
ones = torch.ones_like(b_x)
b_X = torch.stack([b_x, ones],dim=2)

# 最小二乗解
b_XtX = torch.bmm(b_X.transpose(1,2),b_X)
b_inv_XtX = torch.inverse(b_XtX)
b_Xty = torch.bmm(b_X.transpose(1,2),b_y[:,:,None])

b_beta_hat = torch.bmm(b_inv_XtX, b_Xty)  # (batch,2,1) であることに注意
print(b_beta_hat)

tensor([[[2.0427],
         [3.0002]],

        [[3.8828],
         [5.2894]]], dtype=torch.float64)

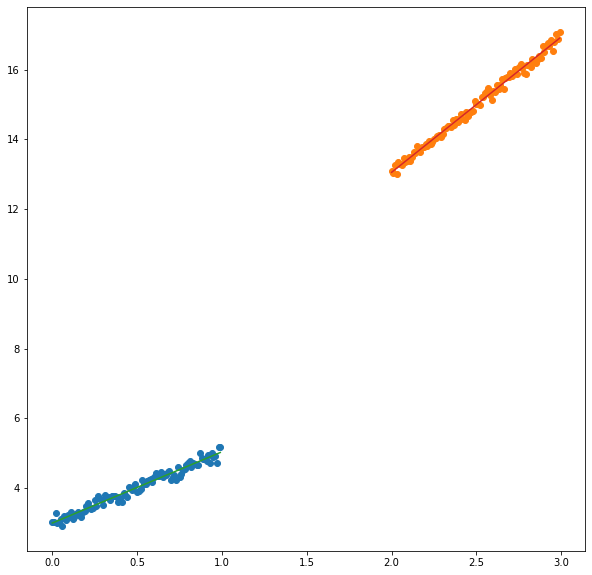
最小二乗解をグラフで表示させます．

b_y_hat = torch.bmm(b_X, b_beta_hat)

fig, ax = plt.subplots(figsize=(10,10))
ax.scatter(x_1.numpy(), y_1.numpy(), color="C0")
ax.scatter(x_2.numpy(), y_2.numpy(), color="C1")

ax.plot(x_1.numpy(), b_y_hat[0,:,:].squeeze(dim=1).numpy(),color="C2")
ax.plot(x_2.numpy(), b_y_hat[1,:,:].squeeze(dim=1).numpy(),color="C3")

[<matplotlib.lines.Line2D at 0x1e86b5e1e88>]

RANSAC

以上の計算を用いて，2次元の直線検出のRANSACを試してみます．手順としては

  • すべての$n$個の点から，$s$点×$m$をサンプリングして$m$個それぞれの最小二乗解(直線)を求める．
  • 各直線について，すべての点との距離を計算し，閾値以内に収まる点の数を求める．
  • 最も閾値以内に収まる点の多い直線を結果とする．

まずnumpyとfor文で実装してからpytorchで実装してみます．

データの作成

($a=2, c=3$)のデータにまとまったノイズが乗ってしまったようなデータとします．

a_1 = 2.0
b_1 = 3.0

a_2 = 2.0
b_2 = 4.0

def func1(x):
    return a_1*x+b_1

def func2(x):
    return a_2*x+b_2

x_1 = np.arange(0,1,0.01)
x_2 = np.arange(0.8,1,0.005)
all_x = np.concatenate([x_1,x_2],axis=0)

y_1 = func1(x_1) + 0.1*np.random.randn(len(x_1))
y_2 = func2(x_2) + 0.2*np.random.randn(len(x_2))
all_y = np.concatenate([y_1,y_2],axis=0)

fig, ax = plt.subplots(figsize=(10,10))
ax.scatter(all_x, all_y, color="C0")

<matplotlib.collections.PathCollection at 0x1e86b5ffc88>

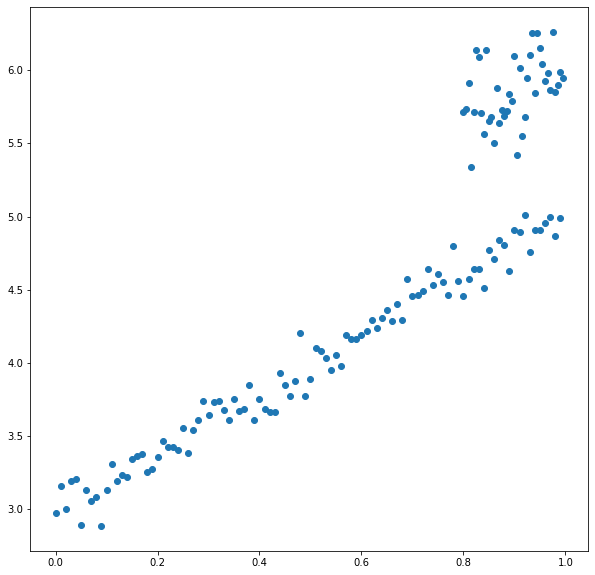
print("all_x length:",len(all_x))

all_x length: 140

サンプリング

直線の本数($m$)×一本の推定に利用する点数($s$)　の分だけデータをサンプリングする必要があります．

line_number = 20  # m
point_number = 5  # s

distance_th = 0.1  # 距離の閾値

非復元抽出としてすべての$m$本の直線で重複の無いサンプリングを行います．しかしlinenumber($m$)×point_number($s$)の数データよりデータ数が大きい必要があります．
numpy.random.permutationはrangeの値をランダムに並べ替えたndarrayを返す関数です．

random_index_flatten = np.random.permutation(len(all_x))[:line_number*point_number]
random_index = random_index_flatten.reshape(line_number, point_number)
# random_index

numpy

for文で回しながら，RANSACを計算します．距離の計算は点と直線の距離の公式を用いています．

distance_vote_list = []
solution_list = []

solution_points_list = []  # おまけ

for points_index in random_index:
    # 利用するデータ
    x = all_x[points_index]
    y = all_y[points_index]
    
    # 計画行列
    X = np.stack([x,np.ones(len(x))],axis=1)

    # 最小二乗解
    inv_XtX = np.linalg.inv(np.dot(X.T,X))
    Xty = np.dot(X.T,y)
    beta_hat = np.dot(inv_XtX, Xty)
    # 距離の計算
    a = beta_hat[0]
    b = - 1
    c = beta_hat[1]
    d_num = a * all_x + b * all_y + c  # (all_point_number(n))
    d_den = np.sqrt(a**2+b**2)  # 1
    d = np.abs(d_num) / d_den  # (all_point_number(n))
    
    # 投票
    vote_number = (d < distance_th).sum()
    
    distance_vote_list.append(vote_number)
    solution_list.append(beta_hat)
    
    solution_points_list.append(np.stack([x,y],axis=1))
    
solution_array = np.stack(solution_list, axis=0)
distance_vote_array = np.array(distance_vote_list)
ransac_solution_index = np.argmax(distance_vote_array,axis=0)

ransac_solution = solution_array[ransac_solution_index]
print("ransac solution:",ransac_solution)

ransac_solution_points = solution_points_list[ransac_solution_index]

ransac solution: [2.08543647 2.92102793]

print(distance_vote_array)

[68 79 78 98 91 65 70 61 67 70 58 67 71 72 61 85 75 84 72 76]

RANSACの計算結果をグラフで表示させます．赤い点は解を求めるのに利用した点です．

all_X = np.stack([all_x,np.ones(len(all_x))],axis=1)
ransac_y_hat = np.dot(all_X, ransac_solution)
fig,ax = plt.subplots()
ax.plot(all_x, ransac_y_hat, color="C1")
ax.scatter(all_x, all_y, color="C0")
ax.scatter(ransac_solution_points[:,0],ransac_solution_points[:,1],color="C3")

<matplotlib.collections.PathCollection at 0x1e86b771e88>

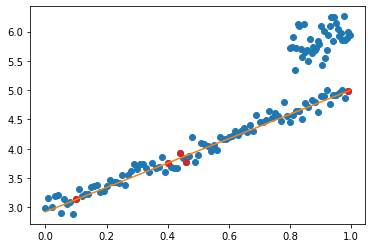
pytorch

ミニバッチとして並列にRANSACを計算します．

all_x_tensor = torch.from_numpy(all_x)  # (all_point_number(n))
all_y_tensor = torch.from_numpy(all_y)  # (all_point_number(n))

b_x = torch.from_numpy(all_x[random_index])  # (line_number(m), point_number(s))
b_y = torch.from_numpy(all_y[random_index])  # (line_number(m), point_number(s))

# 計画行列
ones = torch.ones_like(b_x)
b_X = torch.stack([b_x, ones],dim=2)

# 最小二乗解
b_XtX = torch.bmm(b_X.transpose(1,2),b_X)
b_inv_XtX = torch.inverse(b_XtX)
b_Xty = torch.bmm(b_X.transpose(1,2),b_y[:,:,None])

b_beta_hat = torch.bmm(b_inv_XtX, b_Xty)  # (batch,2,1) であることに注意
b_beta_hat_squeezed = b_beta_hat.squeeze(2)  # (batch,2)

# 距離の計算
a = b_beta_hat_squeezed[:,0]  # (line_number(m))
c = b_beta_hat_squeezed[:,1]  # (line_number(m))
d_num = a[:,None] * all_x_tensor[None,:]  - all_y_tensor[None,:] + c[:,None]  # (line_number(m), all_point_number(n))
d_den = torch.sqrt(a**2+(-1)**2)  # (line_number(m))
d = torch.abs(d_num) / d_den[:,None]

# 投票
b_vote_number = (d < distance_th).sum(dim=1)  # (line_number(m))
ransac_solution_index = np.argmax(b_vote_number.numpy(),axis=0)  # 正確な比較のためにnumpyで計算

ransac_solution = b_beta_hat_squeezed[ransac_solution_index].numpy()
print("ransac solution:", ransac_solution)

solution_points = torch.stack([b_x[ransac_solution_index,:],b_y[ransac_solution_index,:]],dim=1)

ransac solution: [2.08543647 2.92102793]

ここで注意しなければならないのは距離の計算でブロードキャストを用いていることです．
RANSACの計算結果をグラフで表示させます．

all_X = np.stack([all_x,np.ones(len(all_x))],axis=1)
ransac_y_hat = np.dot(all_X, ransac_solution)
fig,ax = plt.subplots()
ax.plot(all_x, ransac_y_hat, color="C1")
ax.scatter(all_x, all_y, color="C0")
ax.scatter(solution_points[:,0].numpy(),solution_points[:,1].numpy(),color="C3")

<matplotlib.collections.PathCollection at 0x1e86b7afd48>

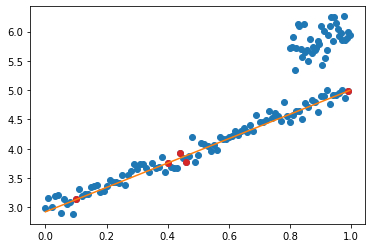
おまけ(全ての点を利用した最小二乗法)

RANSACを用いない場合の計算をしてみます．

# 計画行列
X = np.stack([all_x,np.ones(len(all_x))],axis=1)

# 最小二乗解
inv_XtX = np.linalg.inv(np.dot(X.T,X))
Xty = np.dot(X.T,all_y)
beta_hat = np.dot(inv_XtX, Xty)
print(beta_hat)

[2.96600878 2.71063865]

y_hat = np.dot(X, beta_hat)

fig, ax = plt.subplots()
ax.scatter(all_x,all_y)
ax.plot(all_x,y_hat,color="C1")

[<matplotlib.lines.Line2D at 0x1e86b877e48>]

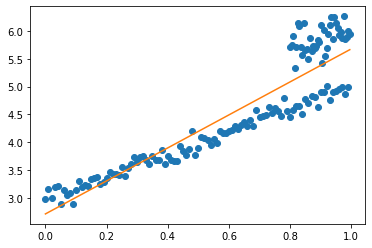
このようにノイズにひっばられてしまいます．

まとめ

  • Pytorchを利用してfor文を用いずにRANSACを実装しました．
1
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?