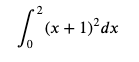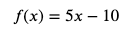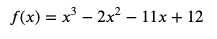GCIデータサイエンティスト育成講座の解答を作ってみた(5章) #Python

松尾研究室のGCIデータサイエンティスト育成講座やってみた

解答が無かったので、自分で作ってみました。間違えていたらすみません、教えて頂けると嬉しいです
https://weblab.t.u-tokyo.ac.jp/gci%E3%83%87%E3%83%BC%E3%82%BF%E3%82%B5%E3%82%A4%E3%82%A8%E3%83%B3%E3%83%86%E3%82%A3%E3%82%B9%E3%83%88%E8%82%B2%E6%88%90%E8%AC%9B%E5%BA%A7%E3%83%BB%E6%BC%94%E7%BF%92%E3%82%B3%E3%83%B3%E3%83%86/

5.3.1 Scipy

<練習問題 1>
以下のデータに対して、線形補間の計算をして、グラフを描いてください。
<練習問題 2>
2次元のスプライン補間をして上記のグラフに書き込んでください(2次元のスプライン補間はパラメタをquadraticとします。)

x = np.linspace(0, 10, num=11, endpoint=True)
y = np.sin(x**2/5.0)
plt.plot(x,y,'o')
plt.grid(True)
x1 = np.linspace(0, 10, num=100, endpoint=True)
f=interpolate.interp1d(x, y,'linear')
f2=interpolate.interp1d(x, y,'cubic')
plt.plot(x1,f(x1),"-",x1,f2(x1),"--")

<練習問題 1>
以下の行列に対して、特異値分解をしてください。
B = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])

B = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
U, s, Vs = sp.linalg.svd(B)
m, n = B.shape
S = sp.linalg.diagsvd(s,m,n)
print("U.S.V* = \n\n",U@S@Vs)

<練習問題 2>
以下の行列に対して、LU分解をして、 𝐴𝑥=𝑏 の方程式を解いてください。

#データの準備
A = np.identity(3)
print(A)
A[0,:] = 1
A[:,0] = 1
A[0,0] = 3
b = np.ones(3)
(LU,piv) = sp.linalg.lu_factor(A)
L = np.identity(3) + np.tril(LU,-1)
U = np.triu(LU)
P = np.identity(3)[piv]
# 解を求める
x = sp.linalg.lu_solve((LU,piv),b)

<練習問題 1>
以下の積分を求めてみましょう。

integrate.quad(lambda x:(x+1)**2,0,2)

<練習問題 2>
cos関数の範囲 (0,𝜋) の積分を求めてみましょう。

from numpy import cos
integrate.quad(cos,0,math.pi/1)

<練習問題 1>
以下の関数が0となる解を求めましょう。

def f(x):
    return 5*x-10
sol1=fsolve(f,0)
print(sol1)

<練習問題 2>
以下の関数が0となる解を求めましょう。

def f2(x):
    return x**3-2*x**2-11*x+12
sol2=fsolve(f2,0)
print(sol2)

5.4 総合問題
5.4.1 総合問題1
以下の行列に対して、コレスキー分解を活用して、𝐴𝑥=𝑏の方程式を解いてください。

A = np.array([[5, 1, 0, 1],
              [1, 9, -5, 7],
              [0, -5, 8, -3],
              [1, 7, -3, 10]])
b = np.array([2, 10, 5, 10])


L = sp.linalg.cholesky(A)

t = sp.linalg.solve(L.T.conj(), b)
x = sp.linalg.solve(L, t)

# 解答
print(x)
[-0.051  2.157  2.01   0.098]