金子勇さんのED法のシンプルな解説を試みた

はじめに

@pocokhc(ちぃがぅ)さんが、金子勇さんのED法を実装してMNISTの学習に成功しました。

金子勇さんの失われたED法

金子勇さんの失われたED法発掘の経緯

ここではちぃがぅさんのコードを元に、ED法をシンプルに解説していきたいと思います。

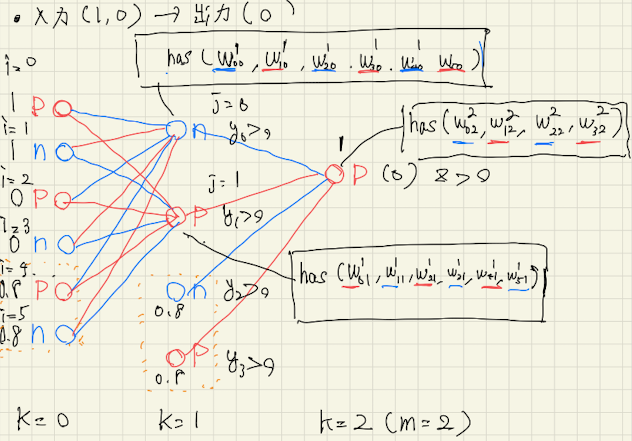
ED法をわかりやすく解説するため、今入力を(1,0)としたとき(0)を推論するXOR問題を考えてみましょう。

ED法の場合, 入力、重みともに正負(p,n)２つ分の変数を用意する必要があります。

例えば　

入力を(1,0)とすると

1 (p) ,1 (n), 0 (p), 0 (n) の4つとバイアス分の2つの p n が必要です。

また, 3層構造として中間層のニューロンをp, n 2つのみとします。

中間層のニューロンを２つとしたときは、

p, n の２つと, バイアス用のp, n の２つが必要です。

中間層のニューロン各々は、そのニューロンから見て下流のニューロン全てに対する重みを保持します。

この図の場合は, 中間層のニューロンが２つならそれぞれ6つのニューロンを持つので, 全部で12個の重みを中間層は保持しています。

この図では出力は1つのpのニューロンですが, 下流に４つのニューロンがあるので重みは４つあります。

(1) Forwardの計算

フォワードを計算してみましょう。

中間層では２つのニューロンに対する積和計算が行われますので、

$y_0=\sigma\left(
x_0 \cdot {\color{blue} w_{00}^1} + x_1 \cdot {\color{red} w_{10}^1} + x_2 \cdot {\color{blue}w_{20}^1} + x_3 \cdot {\color{red} w_{30}^1} + x_4 \cdot {\color{blue}w_{40}^1} + x_5 \cdot {\color{red} w_{50}^1} \right)$

$y_1=\sigma\left(x_0 \cdot {\color{red} w_{01}^{1}}+x_1 \cdot {\color{blue} w_{11}^{1}}+x_2 \cdot {\color{red} w_{21}^{1}}+x_3 \cdot {\color{blue} w_{31}^{1}}+x_4 \cdot {\color{red} w_{41}^{1}}+x_5 \cdot {\color{blue} w_{51}^{1}}\right)$

となります。(ここで$\sigma$はシグモイド関数です, 右上の添字は層の番号です）
重みは自分自身のニューロンの極性と自分から見た相手への極性から重みの正負が決まります。
例えば図ですと中間層の最初(j=0)のニューロンは負(n)であり、そこから入力の最初(i=0)のニューロンは正(p)なので重みには-をかけて負にします。
次は　j=0における負のニューロンからi=1における負のニューロンを見たときは正となるので、重みは正となります。
上の式では正負どちらの重みになっているか色付けしてあります。

出力層(mを出力層とします)では、中間層で得た$y_0$,$y_1$にバイアスの$y_2$,$y_3$に対する重みとの積和演算が行われ

$o^m=\sigma\left( y_0 \cdot {\color{blue} w_{02}^2} + y_1 \cdot {\color{red} w_{12}^2} + y_2 \cdot {\color{blue} w_{22}^2} + y_3 \cdot {\color{red} w_{32}^2} \right)$

が得られます。

(2) Backwardの計算

出力層における教師信号 $y$ と$o^m$ との2乗誤差を以下で定義します。

$E = \frac{1}{2}(y - o^m)^2$

ここで、以下のように定義します。

$d^m=-\frac{\partial E}{\partial o^m}=y-o^m$

（プログラム中ではdiff = target -x )

以下は、重みの更新の式です。

$w_{ij}^k \leftarrow w_{ij}^k - \epsilon \frac{\partial E}{\partial w_{ij}^k}$

ここで, $\epsilon$は学習率と呼ばれるハイパーパラメータです。

この重みのわずかな変化量$\frac{\partial E}{\partial w_{ij}^k}$を求めることで重みを調節することを試みます。

(3) 重みの更新方法

$d^m=-\frac{\partial E}{\partial o^m}=y-o^m$

の出力層は

もし

$y - o^m > 0$ ならば(興奮性とし）
$d^{m+} = y - o^m$
$d^{m-} = 0$
とし、正の重みだけをupdateします。

$y -o^m < 0$ ならば（抑制性とし）
$d^{m+} = 0$
$d^{m-} = o^m - y$
とし, 負の重みだけをupdateします。

具体的には, $d$を求めた後, 上流から下流へ重みをupdateしていきます。

(a) 興奮性細胞からの結合の場合（正の重みのみをupdateする)：

$\Delta w_{i j}^k = -\epsilon \frac{\partial E}{\partial w_{i j}^k}$
$= -\epsilon \frac{\partial E}{\partial o_j^k} \cdot \frac{\partial o_j^k}{\partial i_j^k} \cdot \frac{\partial i_j^k}{\partial w_{i j}^k}$
$= \epsilon \cdot d_j^{k+} \cdot f^{\prime} (o_j^k) \cdot o_i^{k-1} \cdot \operatorname{sign}(w_{i j}^k)$

を計算することで、正の重みのみをupdateします。

ここで

$d_j^{k+} = -\frac{\partial E}{\partial o_j^k}$
$f^{\prime}\left(o_j^k\right) = \frac{\partial o_j^k}{\partial i_j^k}$
$o_i^{k-1} = \frac{\partial i_j^k}{\partial w_{i j}^k}$

です。

また、$\operatorname{sign}\left(w_{i j}^k\right)$ は重みの符号を保持するために導入されています。

• $k$は層番号
• $i$は接続元のニューロンのindex
• $j$は接続先のニューロンのindex
• $w$が重み（重みが興奮性の場合, self.weights[idx]で正の重みのみを取り出します)
• $\epsilon$が学習率 (プログラム中ではself.alpha）
• $o_i^{k-1}$が接続元のニューロンの出力値 (プログラム中ではself.prev_in[idx])
• $o_j^k$が接続先のニューロンの出力値
• $f^{\prime} (o_j^k)$は, 接続先のニューロンの出力値の微分 (プログラム中ではgrad)
• $d$は、教師データと最終的な出力値の差分 (プログラム中ではdelta_out)
• $\operatorname{sign}(w_{i j}^k)$ 今いるニューロンから見た相手先のニューロンの極性(プログラム中ではself.weights_operator[idx]）
• プログラム中のself.operatorは、今いるニューロンの極性

(b) 抑制性細胞からの結合の場合（負の重みのみをupdateする)：

$d_j^{k+}$ の代わりに $d_j^{k-}$ を使用します。

$\Delta w_{i j}^k = -\epsilon \frac{\partial E}{\partial w_{i j}^k}$
$= -\epsilon \frac{\partial E}{\partial o_j^k} \cdot \frac{\partial o_j^k}{\partial i_j^k} \cdot \frac{\partial i_j^k}{\partial w_{i j}^k}$
$= \epsilon \cdot d_j^{k-} \cdot f^{\prime}(o_j^k) \cdot o_i^{k-1} \cdot \operatorname{sign}(w_{i j}^k)$

ここで、$d_j^{k-} = -\frac{\partial E}{\partial o_j^k}$ です。

を計算することで、負の重みのみをupdateします。

@pocokhc(ちぃがぅ)さんの以下のプログラムコードが参考になります。

def train(self, inputs, target):
        x = self.forward(inputs)

        # --- update(ED)
        diff = target - x
        if diff > 0:
            direct = "upper"
        else:
            direct = "lower"
            diff = -diff
        self.out_neuron.update_weight(diff, direct)
        for h in self.hidden_neurons:
            h.update_weight(diff, direct)

def update_weight(self, delta_out, direct: str):
        grad = self.activation_derivative(abs(self.prev_out))

        if direct == "upper":
            indices = self.upper_idx_list
        else:
            indices = self.lower_idx_list

        for idx in indices:
            # weight選択が行われている　
            # uppderなら自分から相手をみたときの極性が正の重みだけを選択
            delta = self.alpha * self.prev_in[idx]
            # 今いるニューロンの極性と相手先のニューロンの極性との掛け算
            delta *= grad * delta_out * self.operator * self.weights_operator[idx]
            self.weights[idx] += delta

中間層が2個しかないものすごくシンプルな計算ですがそれでもXORの精度は以下となりました。

--- result ---
[ 0.00, 0.00] ->  0.98, target  1.00
[ 1.00, 0.00] ->  0.01, target  0.00
[ 0.00, 1.00] ->  0.03, target  0.00
[ 1.00, 1.00] ->  0.99, target  1.00

ED法は正負２つのニューロンを用いるということで面白いなと思いました。

数式展開でわかりにくいところについて

金子さんのWebには式導出の経緯が失われていたりするのでそこを補完します。

疑問１

どうして　

$\frac{\partial i_j^k}{\partial w_{ij}^k} = o_i^{k-1}$　

が成り立つの？

まず前提として

• $o_i^k =f\left(i_i^k\right)$
• $i_j^k =\sum_i w_{i j}^k o_i^{k-1}$

です。
各記号の意味は以下の通りです：

• $i_i^k$：$k$層目の$i$番目のニューロンの入力
• $o_i^k$：$k$層目の$i$番目のニューロンの出力
• $w_{ij}^k$: $k-1$層目の$i$番目のニューロンから$k$層目の$j$番目のニューロンへの結合重み

まず$i_j^k$の定義から直接偏微分を取ると、

$\frac{\partial i_j^k}{\partial w_{ij}^k} = \frac{\partial}{\partial w_{ij}^k}\left(\sum_i w_{ij}^k o_i^{k-1}\right)$

この和の中で$w_{ij}^k$ の偏微分を考えるとき,和の中の各項は異なる $w_{ij}^k$に対応します。　したがって,特定の$w_{ij}^k$に関してのみ偏微分を考える場合,それ以外の重みが消え, 特定の$w_{ij}^k$に関してのみ残ります。
従って
$\frac{\partial i_j^k}{\partial w_{ij}^k} = \frac{\partial}{\partial w_{ij}^k}\left(w_{ij}^k o_i^{k-1}\right) = o_i^{k-1}$
となります。
つまり$\frac{\partial i_j^k}{\partial w_{ij}^k}$は前の層の$i$番目のニューロンの出力$o_i^{k-1}$に等しくなります。

疑問2　

$\frac{\partial o_j^k}{\partial i_j^k} = f'(o_j^k)$　

は正しいのか？

おそらく記述ミスの可能性が高い？

$\frac{\partial o_j^k}{\partial i_j^k} = f'(i_j^k)$　

調査が必要。

生理学的な考察に対して

において　@obgynengine(H O)さんが生理学的なメモを残しています。

これらに関する面白い結果として　ハーバード大学の研究を紹介したナゾロジーの記事があります。

元論文

この研究が明らかにしたのは, 意思決定の仕組みを世界で初めて観測により実証したことです。記事の一部を少し改変して紹介しますと,

脳のネットワーク内部には「興奮性ニューロン」と「抑制性ニューロン」があります。

マウスの実験において,

• マウスが右折を決めた時には, そのなかの一部の興奮性ニューロン（右折ニューロン）が発火し,同時に左折を決めた時に興奮するはずだった左折ニューロンを抑制する抑制性ニューロンを起動させました。
• 逆に左折を決めた時には,左折ニューロンが興奮すると同時に右折ニューロンを抑制する抑制性ニューロンが起動していました。

この結果は, 意思決定を行う神経ネットワークには, それぞれの選択に対応して興奮するニューロンたち（右折ニューロンと左折ニューロン）が存在すること、また同時に、それらのニューロンたちは, 選ばれなかったほうのニューロンの動きを抑制していたということです。

つまり意思決定では選んだほうの活性化と選ばなかったほうの抑制化がセットで起きていたわけです。

そう考えると金子さんのED法は理にかなった方法と言えるのではないのでしょうか。
今後1bit NNの成果と融合することで新規性ある研究や技術発展に貢献するものと思われます。