この記事について
DeepMind が Nature に投稿した論文
Hybrid computing using a neural network with dynamic external memory
で使用されている "Differentiable Neural Computing (DNC)" について解説します。ロジックの説明がメインですが、Python - Chainer による実装例も紹介します。
Differentiable Neural Computing (DNC)とは
sequential data を Neural Net で処理したいという欲求は昔からあるようで、一番スタンダードなものは Recurrent Neural Net (RNN) です。しかし、RNN には"勾配消失問題"というものがありまして、それを克服したモデルが Long Short Term Memory (LSTM) と呼ばれています。何が short で何が long なのかというと、入力されたデータは、出力されるまで Neural Net の内部にとどまっているわけです。これはある意味で "Memory" のようなものと考えてもよさそうです。しかし、入力から出力までの"短時間"しか記憶ができない。なので、"short term momory" と呼ばれます。「この short term memory の記憶できる時間が長くなりましたよ」という意味で、Long Short Term Memory と名付けられているようです。そうすると、本当に long な Meomory は学習機内部ではなくて外部にあってもいいかもしれない、そんな気がしてきます。そういう思いから生まれた、かどうかは分かりませんが、Differentiable Neural Computing (DNC) とは、学習機の外部に Memory を用意してやって、Memory の使用法まで含めて学習させてしまうというものです。"Differentiable"の意味ですが、back propagation で学習させようと思うと、微分を計算できることが必要になります。ですので、外部 Memory に対する操作も含めて"微分計算が可能であること"という意味です。
ロジック解説
DNC の全体像
DNC の構成要素は、本体である Controller と外部 Memory です。論文によると、全体としてのデータの流れは下図のように表すことができます。
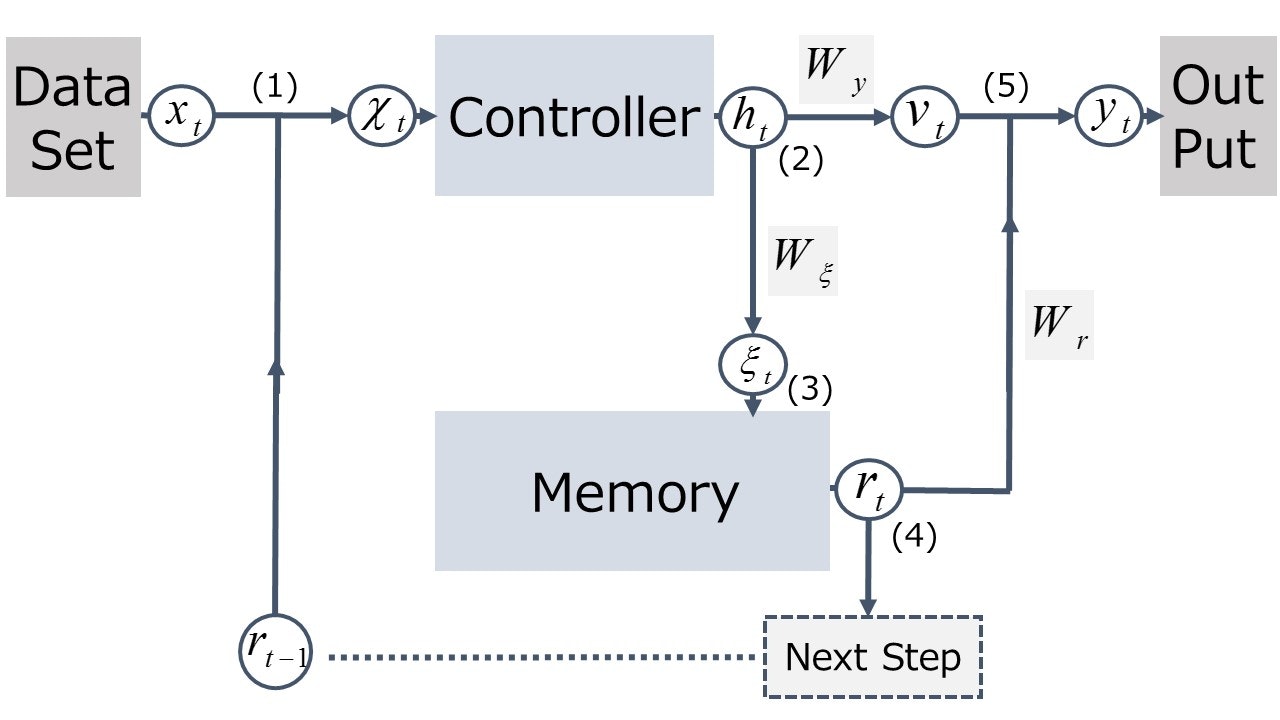
DNC は sequential data を扱いますので、現在の time-step を $t$ と表しています。前 step は $t-1$、次 step は $t+1$ となり、図中の添え字 $t$ は、それぞれの変数がどの time-step で生成されたものであるかを表しています。
それでは、データの流れを順を追って見ていきましょう。図中に(1)~(4)の番号が振ってありますので、この順で追ってください。
(1) : "Data Set" より 入力データ $x_t$ が入力されます。これに、前 step での Memory からの出力 $\boldsymbol{r}_{t-1}$ とを合わせた $\boldsymbol{\chi}_t=[\boldsymbol{x}_t, \boldsymbol{r}_{t-1}]$ を Controller への入力とします。
(2) : Controller からの出力 $\boldsymbol{h}_t$ が得られますので、これを2つのルートに振り分けます。ひとつは、"Out Put" に向けての $\boldsymbol{v}_t$、もう1つは Memory を制御するための "interface vector" $\boldsymbol{\xi}_t$ です。論文中では、これらは $\boldsymbol{h}_t$ の線形変換 $\boldsymbol{v}_t=W_y \boldsymbol{h}_t$ と、$\boldsymbol{\xi}_t=W_{\xi} \boldsymbol{h}_t$ として書かれています。
(3) : "interface vector" $\boldsymbol{\xi}_t$ をもとに Memory へのデータの書き込みが行われ Memory の状態が更新されます。また、Memory からの読み出しも行われ、"read vector" $\boldsymbol{r}_t$ が得られます。
(4) : "read vector" $\boldsymbol{r}_t$ は、 "Out Put"への出力に加算される一方で、次 step での Controller への入力へと回されます。
(5) : Controller からの出力と、Memoryからの出力を合成し"Out Put" へ $\boldsymbol{y}_t = \boldsymbol{v}_t + W_r \boldsymbol{r}_t$ を出力します。
以上、(1)~(5) をもって、1 step が完了します。
Controller としては、多次元の入力を受け取り、多次元の出力を返す学習機なら何でもよいのですが、(Recurrent) Neural Net や LSTMなどを使うことが多いようです。(Recurrent) Neural Net や LSTM の解説は他にゆずるとして、この記事では、DNC の最大の特徴である「外部 Memory の読み書き」について解説していきます。
外部 Memory の読み書きについて
それでは、外部 Memory の読み書きについて解説しましょう。面倒なので、以下では単に Memory と呼ぶことにします。
Memory の構造
まずは、Memory の構造について把握しておきましょう。
Memory としては $N$ × $W$ の行列を用います。つまり、address が $1$~$N$ まで振られていて、各 address に $W$ 次元の数値ベクトルを格納できる slot があると考えます。Memory の状態は刻々と更新されていきますので、time-step $t$ での Memory を表す行列を $M_t$ と書くことにします。ただし、行列の次元 $N$ × $W$ は固定されているものとし、常に、$N$ は memory slot の総数 (address の総数)、$W$ は slot の長さ(格納する数値ベクトルの次元)とします。
interface vector の詳細
「全体のデータの流れ」でも述べた通り、Controller による Memory の操作は
"interface vector" $\boldsymbol{\xi}_t$ を通して行われます。一口で Memory の操作といっても、読み込み/書き込み/addressの指定など、複数のタスクが考えられますので、$\boldsymbol{\xi}_t$ は機能別に各 component に分解されます。
\begin{align}
\boldsymbol{\xi}_t = \Big[ \boldsymbol{k}_t^{r, 1},...,\boldsymbol{k}_t^{r, R}, \; \hat{\beta}_t^{r, 1},...,\hat{\beta}_t^{r, R}, \; \boldsymbol{k}_t^w, \; \hat{\beta_t}^w, \hat{\boldsymbol{e}}_t, \; \boldsymbol{\nu}_t, \; \hat{f}_t^1,...,\hat{f}_t^R, \; \hat{g}_t^a, \; \hat{g}_t^w, \; \hat{\boldsymbol{\pi}}_t^1,...,\hat{\boldsymbol{\pi}}_t^R \Big]
\end{align}
'$\hat{}$' 記号がついているものは、さらに scale 変換をかけます。種類が多くてややこしいので、いったんまとめます。( , )内の値は、(次元, 個数)です。
・"read key" $(W, R) ; :; \boldsymbol{k}_t^{r, 1},...,\boldsymbol{k}_t^{r, R}$
・"read strength" $(1, R) ; : ; \beta_t^{r, 1},...,\beta_t^{r, R} ;;\big(\beta_t^{r, i}=\text{oneplus}(\hat{\beta}_t^{r, i})\big)$
・"write key" $(W, 1) ; : ; \boldsymbol{k}_t^w$
・"write strength" $(1,1) ; : ; \beta_t^w=\text{oneplus}(\hat{\beta}_t^w)$
・"erase vector" $(W, 1) ; : ; \boldsymbol{e}_t=\sigma(\hat{\boldsymbol{e}}_t)$
・"write vector" $(W, 1) ; : ; \boldsymbol{\nu}_t$
・"free gate" $(1, R) ; : ; f_t^1,...,f_t^R ;; \big(f_t^i=\sigma(\hat{f}_t^i)\big)$
・"allocation gate" $(1, 1) ; :; g^a_t=\sigma(\hat{g}^a_t)$
・"write gate" $(1, 1) ; :; g^w_t=\sigma(\hat{g}^w_t)$
・"read mode" $(3, R) ; : ; \boldsymbol{\pi}_t^1,...,\boldsymbol{\pi}_t^R ;; \big(\boldsymbol{\pi}_t^i=\text{softmax}(\hat{\boldsymbol{\pi}}_t^i)\big)$
スケール変換に用いる関数は、
\begin{align}
& \text{oneplus}(x) = 1+\text{log}(1+e^x) \in [1, \infty) \\
& \sigma(x) = \frac{1}{1+e^{-x}} \in [0, 1] \\
& \text{softmax}(\boldsymbol{x}) = \frac{e^\boldsymbol{x}}{\sum_ie^{x_i}} \in [0, 1]
\end{align}
と定義されています。$\text{oneplus}(x)$、 $\sigma(x)$、$\text{exp}(x)$ の引数にベクトル値を取る場合は、成分ごとの作用を意味しますので注意してください。
ここでは、定義を羅列しただけなので、何もわからないと思います。以下、これらの component をどのように使って Memory を制御していくか、順に解説していきます。
先に進む前に、1点だけ説明を加えておきます。$R$ は Memory からの読み出しの回数を表しています。論文中の DNC では、1 step のうちで Memory からの読み出しを複数回行う設定となっていて、その回数が $R$ です。対して、書き込みは、1 step に1回のみの設定です。また、interface vector の次元は、$W$ と $R$ で決まっていて、$WR+3W+5R+3$ となることも分かるかと思います。
Memory の読み書き手順(概要)
Memory の読み書きには、読み書き対象となる Memory slot の address を指定する必要があります。ただし、back propagation による学習が可能であるためには、微分可能性、少なくとも演算の連続性が必要となります。よって、特定のひとつの address だけを指定するのではなく、幅を持たせて、どの address を重点的に読み込む/書き込むかの重みづけを行います。以後、この重みを、"read/write weighting"と呼ぶことにしますが、これらをどう求めていくかがポイントになります。
"read/write weighting" を求めてしまえば、読み込み/書き込みの演算自体は単純です。詳細は後に回しますが、概要をつかんでおきましょう。まず、読み込みの場合を考えてみます。今、"read weighting" $\boldsymbol{w}^r_t$ が得られたとします。このベクトルの次元は、Memory slot の総数と同じ $N$ です。各成分は対応する address の Memory slot にある情報をどれだけ"強く"読み込むかを表しています。すなわち、読みだされる情報は、Memory 行列と重みベクトルの積として、$M_t^T\boldsymbol{w}^r_t$と表されます。先にも述べましたが、論文中では 1 step で読み出しを $R$ 回行う設定なので、"read weighting" も $R$ 個 $\{\boldsymbol{w}_t^{r,i}\}_{i=1,...,R}$ 構成されます。また、読み出しによる増幅など防ぐため、自然な要請として
\begin{align}
& 0 \leqq \boldsymbol{w}_t^{r,i}[n] \leqq 1 \;\; (n=1,2,...,N)\\
& \sum_{n=1}^N \boldsymbol{w}_t^{r,i}[n] \leqq 1 \;\; (i=1,2,...,R)
\end{align}
を課すものとします。
同様に、書き込みの場合も考えてみましょう。"write weighting" $\boldsymbol{w_t^w}$ が得られたとします。また、書き込みたい情報を表すベクトル $\boldsymbol{\nu}_t$ も得られているとします。$\boldsymbol{w_t^w}$の次元は$N$で、各成分は対応する Memory slot にどれだけ"強く" $\boldsymbol{\nu}_t$ を書き込むかを意味します。つまり、Memory 行列 $M_{t-1}$ に、行列 $\boldsymbol{w_t^w}\boldsymbol{\nu}_t^T$ を加算することで書き込みを行い Memory を更新します。各成分に
\begin{align}
& 0 \leqq \boldsymbol{w}_t^w[n] \leqq 1 \;\; (n=1,2,...,N)\\
& \sum_{n=1}^N \boldsymbol{w}_t^w[n] \leqq 1
\end{align}
を課す点は同様です。
Memory の読み書き手順(詳細)
論文中では、Memory への読み書き自体も含めて以下の4つの手順を踏んでいます。
①write weighting の更新
②Memory への書き込み
③read weighting の更新
④Memory からの読み込み
以下、このステップにそって解説していきますが、実装例でも、この順で処理をまとめていますので、参考にしてください。
尚、前 time-step での read/write weighting $\{\boldsymbol{w}_{t-1}^{r,i}\}_{i=1,...,R}$ / $\boldsymbol{w}_{t-1}^{w}$は得られているものとします。
①write weightingの更新
書き込み先の address の選択には2つの方法があり、write weighting は2つの要素から構成されます。つまり、(1) interface vector を通して入力された "key" をもとに書き込み先 slot を選択、(2)前 time-step までの読み出し状況をもとに使用済みの情報が残っている slot を選択、の2つです。
まずは、(1)から見ていきましょう。
interface vector $\boldsymbol{\xi}_t$ 中の "write key" $\boldsymbol{k}_t^w$ を各 Memory slot に保持されている情報と照合し類似度を計算します。また、weighting の peak の鋭さを調整するパラメータとして "write strength" $\beta_t^w$ も使用します。
この計算は、read weighting を求めるところでも共通なので、$N$×$W$ 行列 $M$、$W$ 次ベクトル $\boldsymbol{k}$、スカラー値 $\beta$ に対して、以下の演算を定義しておきます。
\begin{align}
\mathcal{C}(M, \boldsymbol{k}, \beta)[n] = \frac{\text{exp}\big(\mathcal{D}(\boldsymbol{k}, M[n,:])\beta \big)}{\sum_m\text{exp}\big(\mathcal{D}(\boldsymbol{k}, M[m,:])\beta \big)}
\end{align}
ここで、$\mathcal{D}$ は2つのベクトル間の距離で、とりかたはいろいろ考えられますが、論文に合わせてコサイン類似度
\begin{align}
\mathcal{D}(\boldsymbol{u}, \boldsymbol{v}) = \frac{\boldsymbol{u} \cdot \boldsymbol{v}}{||\boldsymbol{u}|| \; ||\boldsymbol{v}||}
\end{align}
としておきます。$\beta \rightarrow \infty$ の極限で $\mathcal{C}$ は鋭いピークがひとつだけ立ちます。
さて、ここで定義した演算を用いて、(1)の方法による write weighting は
\begin{align}
\boldsymbol{c}_t^w=\mathcal{C}(M_{t-1}, \boldsymbol{k}_t^w, \beta_t^w)
\end{align}
と計算されます。
次に(2)の方法による計算です。多少ややこしいですが、以下の順で求めていきます。
(2)-1. "retention vector" $\boldsymbol{\psi}_t$ の構成
前 time-step $t-1$ で情報を読み出した Memory slot は、使用済み slot として書き込みに利用したいと思うのは自然でしょう。しかし、今後も必要な情報が保持されている場合は、上書きしてはいけません。このように、前 time-step で読み込みを行った Memory slot を本当に開放して良いかどうかのフラグ(実際には0~1の連続値なので重み)が "free gate" $f_t^i;(i=1,...,R)$ です。すなわち、$f_t^i \boldsymbol{w}_{t-1}^{r,i}$ を成分単位で考えて、「$f_t^i w_{t-1}^{r,i}$ $\simeq 1$ $\Leftrightarrow f_t^i \simeq 1$ and $w_{t-1}^{r,i}\simeq 1$」 ならば読み込み済みかつ開放OKなので上書きします。また、「$f_t^i w_{t-1}^{r,i}$ $\simeq 0$ $\Leftrightarrow f_t^i \simeq 0$ or $w_{t-1}^{r,i}\simeq 0$」 ならば 前 time-step で読み込まれていない、または、読み込み済みだったとしても解放フラグが立っていないので上書き不可となります。今、各回の読み込みごとに考えていましたが、全 $R$ 回をひっくるめての使用中(上書き不可)フラグである "retention vector" $\boldsymbol{\psi}_t$を
\begin{align}
\boldsymbol{\psi}_t = \prod_{i=1}^R\big(1-f_t^i\boldsymbol{w}_{t-1}^{r, i}\big)
\end{align}
で定義します。積は成分ごとの積をとります。1からの差を求めた後で積を計算していますので、$R$ 回のうち1度でも上書き可と判断された memory slot は上書き可と判断されます。一方で、使用中(上書き不可) $\psi_t \simeq 1$ と判断されるのは、$R$ 回全てについて上書き不可と判断されたときに限られます。
(2)-2. "usage vector" $\boldsymbol{u}_t$ の構成
(2)-1では、使用中フラグ(正しくは重み)としての $\boldsymbol{\psi}_t$ を考えましたが、前 time-step での読み込みについてしか考えていませんでした。実際には、書き込みが行われた場合には使用中の度合いが高まるはずですし、直前 time-step より前の time-step での状況も考えるべきです。これらを踏まえて、各 Memory slot の使用中度合いを表す重み "memory usage vector" $\boldsymbol{u}_t$ を以下の更新式で定義します。
\begin{align}
\boldsymbol{u}_t &= \big(\boldsymbol{u}_{t-1} + \boldsymbol{w}_{t-1}^w - \boldsymbol{u}_{t-1} \circ \boldsymbol{w}_{t-1}^w \big) \circ \boldsymbol{\psi}_t \\
\boldsymbol{u}_0 &= 0, \;\; \boldsymbol{w}_0^w = 0
\end{align}
$\circ$は成分ごとの積を表します。(...)内第3項目は $\boldsymbol{u}_t$ の各成分が $1$ を超えないように調整するための補正です。$u_t = 1$ に達すると書き込みによる重みの更新は停止しますし、もし $u_t > 1$ となってしまっても更新により値を減少させます。
(2)-3. "allocation weighting" の構成
使用中度合い $\boldsymbol{u}_t$ に基づいて、書き込みを行う Memory slot の address を決めます。基本的には、使用中度合いが低いところに書き込む訳ですが、傾斜をつけます。まず、$\boldsymbol{u}_t$ の成分を値が小さい順に並べた時の index からなるベクトルを $\boldsymbol{\phi}_t$ とします。つまり、
\begin{align}
\boldsymbol{u}_t[\boldsymbol{\phi}_t[1]] \leqq \boldsymbol{u}_t[\boldsymbol{\phi}_t[2]] \leqq
\boldsymbol{u}_t[\boldsymbol{\phi}_t[3]] \leqq \cdots \leqq
\boldsymbol{u}_t[\boldsymbol{\phi}_t[N]]
\end{align}
です。これを用いて、"allocation weighting" $\boldsymbol{a}_t$ を
\begin{align}
\boldsymbol{a}_t[\boldsymbol{\phi}_t[n]] = \big(1-\boldsymbol{u}_t[\boldsymbol{\phi}_t[n]]\big) \prod_{m=1}^{n-1}\boldsymbol{u}_t[\boldsymbol{\phi}_t[m]]
\end{align}
で定義します。積は成分ごとの積をとります。基本的には、$1-\boldsymbol{u}_t$ なので使用済み(書き込み可)の度合いを表す重みとなっています。
以上、(1)と(2)の結果を統合し、write weighting $\boldsymbol{w}_t^w$ を
\begin{align}
\boldsymbol{w}_t^w = g_t^w\big(g_t^a\boldsymbol{a}_t+(1-g_t^a)\boldsymbol{c}_t^w\big)
\end{align}
として更新します。ここで、$g_t^a$ と $g_t^w$ は interface vector $\boldsymbol{\xi}_t$ を通して入力されていたものです。それぞれ、「使用済みフラグ or "key"のどちらに基づいて書き込みを行うか」、「そもそも書き込みを行うか」を制御する gate として働きます。
②Memory への書き込み
write weighting の更新が完了しましたので、Memory に書き込みを行います。ただし、書き込みと同時に古い情報の消去も行います。どの Memory slot を対象とするかの重みづけは、"write weighting" $\boldsymbol{w}_t^w$ で行います。書き込まれるデータは "write vector" $\boldsymbol{\nu}_t$、slot 内のデータをどのようなパターンで消去するかは、erase vector $\boldsymbol{e}_t$ で与えられ、この2つは interface vector を通して入力されています。
Memory 行列 $M_{t-1}$ の消去・書き込みによる更新は以下の式に従って行われます。
\begin{align}
& M_t[n,s] = M_{t-1}[n,s] \big(1-\boldsymbol{w}_t^w[n] \boldsymbol{e}_t[s] \big) + \boldsymbol{w}_t^w[n] \boldsymbol{\nu}_t[s] \\
& \Leftrightarrow M_t = M_{t-1} \circ \big(1-\boldsymbol{w}_t^w \boldsymbol{e}_t^T \big) + \boldsymbol{w}_t^w \boldsymbol{\nu}_t^T
\end{align}
③read weightingの更新
読み込み先の address の選択にも2つの方法があります。つまり、
(1) interface vector を通して入力された "key" をもとに読み込み先 slot を選択、(2)書き込み順に従って slot を選択、の2つです。
(1)については、write weighting の時と同じように "read key" $\{\boldsymbol{k}_t^{r,i}\}_{i=1,2,..,R}$ と "read strength" $\{\beta_t^{r,i}\}_{i=1,2,..,R}$ を用いて、
\begin{align}
\boldsymbol{c}_t^{r, i} = \mathcal{C}\big(M_t, \boldsymbol{k}_t^{r,i}, \beta_t^{r,i}\big) \;\; (i=1,2,...,R)
\end{align}
と計算します。
(2)はやや長いですが、順に説明していきます。
説明の便宜上(2)-2 →(2)-1の順で解説しますが、実装する際は(2)-1 →(2)-2の流れです。
(2)-2. "precedence weighting" の構成
precedence weighting $\boldsymbol{p}_t$ を以下の更新式で定義します。
\begin{align}
& \boldsymbol{p}_0 = 0 \\
& \boldsymbol{p}_t = \Big(1-\sum_{n=1}^N \boldsymbol{w}_t^w[n]\Big)\boldsymbol{p}_{t-1} + \boldsymbol{w}_t^w
\end{align}
$\boldsymbol{w}_t^w$ はすでに①で更新が完了していることに注意してください。②で"強く"書き込みが行われた場合は、$\sum \boldsymbol{w}_t^w \simeq 1$ となるので、前 time-step の情報 $\boldsymbol{p}_{t-1}$ は消去され、現 time-step でどこに書き込みが行われたかが保存されます。書き込みが行われなかった場合は、最後に行われた書き込みの重みが保持され続けます。また、$\boldsymbol{p}_t[n] \leq 1$、$\sum_n \boldsymbol{p}_t[n] \leq 1$ であることはすぐにわかります。
(2)-1. "temporal link matrix" の構成
Memory slot への書き込み順を表す $N$ × $N$ 行列 $L_t$ を構成します。成分単位でみたときに $L_t[n, m] \simeq 1$ であることは 「Memory $M_t$ において slot 'n' にある情報は slot 'm' にある情報 の次に書き込まれたものである」という関係が表現できるように、更新式を以下で与えます。
\begin{align}
& L_0[n,m]=0 \\
& L_t[n,n]=0 \\
& L_t[n,m]=\big(1-\boldsymbol{w}_t^w[n]-\boldsymbol{w}_t^w[m]\big)L_{t-1}[n,m] + \boldsymbol{w}_t^w[n]\boldsymbol{p}_{t-1}[m]
\end{align}
対角成分は意味をなさないため $0$ で固定します。$0 \leqq L_t[n,m] \leqq 1$ および、$\sum_m L_t[n,m] \leqq 1$ はすぐに確かめられます。$\sum_n L_t[n,m] \leqq 1$ は確かめようとしましたが、示せませんでした。示せた方がおられましたら、コメントいただけると助かります。
(2)-3. "forward/backward weighting" の構成
Memory への書き込み順を考慮した forward/backward weighting $\{\boldsymbol{f}_t^i\}_{i=1,..,R}$ / $\{\boldsymbol{b}_t^i\}_{i=1,..,R}$をやや荒っぽいですが
\begin{align}
&\boldsymbol{f}_t^i[n]=\sum_{m=1}^NL_t[n,m]\boldsymbol{w}_{t-1}^{r,i}[m] \; \Leftrightarrow \; \boldsymbol{f}_t^i=L_t\boldsymbol{w}_{t-1}^{r,i} \\
&\boldsymbol{b}_t^i[m]=\sum_{n=1}^N\boldsymbol{w}_{t-1}^{r,i}[n]L_t[n,m] \; \Leftrightarrow \; \boldsymbol{b}_t^i=L_t^T\boldsymbol{w}_{t-1}^{r,i} \\
\end{align}
で構成します。$\sum_n L_t[n,m] \leqq 1$ が成り立つならば、$0\leqq \boldsymbol{f}_t^i[n] \leqq 1$ および $\sum_n\boldsymbol{f}_t^i[n]\leqq1$ が成立します。$\boldsymbol{b}_t^i$ についても同様です。
以上、(1)~(2)を統合して、read weighting $\{\boldsymbol{w}_t^{i,r}\}_{i=1,...,R}$ を更新します。
\begin{align}
\boldsymbol{w}_t^{r,i}=\boldsymbol{\pi}_t^i[1]\boldsymbol{b}_t^i + \boldsymbol{\pi}_t^i[2]\boldsymbol{c}_t^i + \boldsymbol{\pi}_t^i[3]\boldsymbol{f}_t^i \;\; (i=1,2,...,R)
\end{align}
$\{\pi_t^i\}_{i=1,...,R}$ は interface vector を通して入力されています。
④Memoryからの読み込み
Memory からの読み出しは簡単です。読み出し結果の "read vector" $\{\boldsymbol{r}_t^i\}_{i=1,..,R}$ は
\begin{align}
\boldsymbol{r}_t^i[s] = \sum_{n=1}^N \boldsymbol{w}_t^{r,i}[n]M_t[n,s] \; \Leftrightarrow \; \boldsymbol{r}_t^i = M_t^T\boldsymbol{w}_t^{r,i} \;\; (i=1,2,...,R)
\end{align}
と計算されます。
以上をもって、time-step $t$ の Memory 読み書きが完了します。
Pyhthon - Chainer による実装例
上で説明したロジックの python による実装例を紹介します。オリジナルのコードは、
DNC (Differentiable Neural Computers) の概要 + Chainer による実装
にあるものです。上の解説と比較しやすいように処理を関数にまとめたり、変数名を変えたりしていますが、内容はほぼ同じものです。
ひとつ注意しておきたいのですが、全体像で示した Controller からの出力 $\boldsymbol{h}_t$ は、論文では Controller の最終的な出力だけでなく、hidden layer の出力もすべて統合しているように見えます。しかし簡単のため、ここで使う Controller は 2層程度の簡単なものに限り、hidden layer の出力は Controller の外には取り出しません。
DNC の実装
import numpy as np
import chainer
from chainer import functions as F
from chainer import links as L
from chainer import optimizers, Chain, Link, Variable
# controller of DNC
class SimpleLSTM(Chain):
def __init__(self, d_in, d_hidden, d_out):
super(SimpleLSTM, self).__init__(
l1 = L.LSTM(d_in, d_hidden),
l2 = L.Linear(d_hidden, d_out),
)
def __call__(self, x):
return self.l2(self.l1(x))
def reset_state(self):
self.l1.reset_state()
class DNC(Chain):
def __init__(self, X, Y, N, W, R):
self.X = X # input dimension
self.Y = Y # output dimension
self.N = N # number of memory slot
self.W = W # dimension of one memory slot
self.R = R # number of read heads
self.d_ctr_in = W*R+X # input dimension into the controller
self.d_ctr_out = Y+W*R+3*W+5*R+3 # output dimension from the controller
self.d_ctr_hidden = self.d_ctr_out # dimension of hidden unit of the controller
self.d_interface = W*R+3*W+5*R+3 # dimension of interface vector
self.controller = SimpleLSTM(self.d_ctr_in, self.d_ctr_hidden, self.d_ctr_out)
super(DNC, self).__init__(
l_ctr = self.controller,
l_Wy = L.Linear(self.d_ctr_out, self.Y),
l_Wxi = L.Linear(self.d_ctr_out, self.d_interface),
l_Wr = L.Linear(self.R * self.W, self.Y),
)
self.reset_state()
def reset_state(self):
# initialize all the recurrent state
self.l_ctr.reset_state() # controller
self.u = Variable(np.zeros((self.N, 1)).astype(np.float32)) # usage vector (N, 1)
self.p = Variable(np.zeros((self.N, 1)).astype(np.float32)) # precedence weighting (N, 1)
self.L = Variable(np.zeros((self.N, self.N)).astype(np.float32)) # temporal memory linkage (N, N)
self.Mem = Variable(np.zeros((self.N, self.W)).astype(np.float32)) # memory (N, W)
self.r = Variable(np.zeros((1, self.R*self.W)).astype(np.float32)) # read vector (1, R * W)
self.wr = Variable(np.zeros((self.N, self.R)).astype(np.float32)) # read weighting (N, R)
self.ww = Variable(np.zeros((self.N, 1)).astype(np.float32)) # write weighting (N, 1)
# utility functions
def _cosine_similarity(self, u, v):
# cosine similarity as a distance of two vectors
# u, v: (1, -) Variable -> (1, 1) Variable
denominator = F.sqrt(F.batch_l2_norm_squared(u) * F.batch_l2_norm_squared(v))
if (np.array_equal(denominator.data, np.array([0]))):
return F.matmul(u, F.transpose(v))
return F.matmul(u, F.transpose(v)) / F.reshape(denominator, (1, 1))
def _C(self, Mem, k, beta):
# similarity between rows of matrix Mem and vector k
# Mem:(N, W) Variable, k:(1, W) Variable, beta:(1, 1) Variable -> (N, 1) Variable
N, W = Mem.shape
ret_list = [0] * N
for i in range(N):
# calculate distance between i-th row of Mem and k
ret_list[i] = self._cosine_similarity(F.reshape(Mem[i,:], (1, W)), k) * beta
# concat horizontally because softmax operates along the direction of axis=1
return F.transpose(F.softmax(F.concat(ret_list, 1)))
def _u2a(self, u):
# convert usage vector u to allocation weighting a
# u, a: (N, 1) Variable
N = u.shape[0]
phi = np.argsort(u.data.flatten()) # u.data[phi]: ascending
a_list = [0] * N
cumprod = Variable(np.array([[1.0]]).astype(np.float32))
for i in range(N):
a_list[phi[i]] = cumprod * (1.0 - F.reshape(u[phi[i]], (1, 1)))
cumprod *= F.reshape(u[phi[i]], (1, 1))
return F.concat(a_list, 0)
# operations of the DNC system
def _controller_io(self, x):
# input data from the Data Set : x (1, X) Variable
# out-put from the controller h is split into two ways : v (1, Y), xi(1, W*R+3*W+5*R+3) Variable
chi = F.concat([x, self.r], 1) # total input to the controller
h = self.l_ctr(chi) # total out-put from the controller
self.v = self.l_Wy(h)
self.xi = self.l_Wxi(h)
# interface vector xi is split into several components
(self.kr, self.beta_r, self.kw, self.beta_w,
self.e, self.nu, self.f, self.ga, self.gw, self.pi
) = F.split_axis(self.xi, np.cumsum(
[self.W*self.R, self.R, self.W, 1, self.W, self.W, self.R, 1, 1]), 1) # details of the interface vector
# rescale components
self.kr = F.reshape(self.kr, (self.R, self.W)) # read key (R, W)
self.beta_r = 1 + F.softplus(self.beta_r) # read strength (1, R)
# self.kw : write key (1, W)
self.beta_w = 1 + F.softplus(self.beta_w) # write strength (1, 1)
self.e = F.sigmoid(self.e) # erase vector (1, W)
# self.nu : write vector (1, W)
self.f = F.sigmoid(self.f) # free gate (1, R)
self.ga = F.sigmoid(self.ga) # allcation gate (1, 1)
self.gw = F.sigmoid(self.gw) # write gate (1, 1)
self.pi = F.softmax(F.reshape(self.pi, (self.R, 3))) # read mode (R, 3)
def _up_date_write_weighting(self):
# calculate retention vector : psi (N, 1)
# here, read weighting : wr (N, R) must retain state one step former
psi_mat = 1 - F.matmul(Variable(np.ones((self.N, 1)).astype(np.float32)), self.f) * self.wr # (N, R)
self.psi = Variable(np.ones((self.N, 1)).astype(np.float32))
for i in range(self.R):
self.psi = self.psi * F.reshape(psi_mat[:,i],(self.N,1)) # (N, 1)
# up date usage vector : u (N, 1)
# here, write weighting : ww (N, 1) must retain state one step former
self.u = (self.u + self.ww - (self.u * self.ww)) * self.psi
# calculate allocation weighting : a (N, 1)
self.a = self._u2a(self.u)
# calculate write content weighting : cw (N, 1)
self.cw = self._C(self.Mem, self.kw, self.beta_w)
# up date write weighting : ww (N, 1)
self.ww = F.matmul(F.matmul(self.a, self.ga) + F.matmul(self.cw, 1.0 - self.ga), self.gw)
def _write_to_memory(self):
# erase vector : e (1, W) deletes information on the Memory : Mem (N, W)
# and write vector : nu (1, W) is written there
# write weighting : ww (N, 1) must be up-dated before this step
self.Mem = self.Mem * (np.ones((self.N, self.W)).astype(np.float32) - F.matmul(self.ww, self.e)) + F.matmul(self.ww, self.nu)
def _up_date_read_weighting(self):
# up date temporal memory linkage : L (N, N)
ww_mat = F.matmul(self.ww, Variable(np.ones((1, self.N)).astype(np.float32))) # (N, N)
# here, precedence wighting : p (N, 1) must retain state one step former
self.L = (1.0 - ww_mat - F.transpose(ww_mat)) * self.L + F.matmul(self.ww, F.transpose(self.p)) # (N, N)
self.L = self.L * (np.ones((self.N, self.N)) - np.eye(self.N)) # constrain L[i,i] == 0
# up date prcedence weighting : p (N, 1)
self.p = (1.0 - F.matmul(Variable(np.ones((self.N, 1)).astype(np.float32)), F.reshape(F.sum(self.ww),(1, 1)))) * self.p + self.ww
# calculate forward weighting : fw (N, R)
# here, read wighting : wr (N, R) must retain state one step former
self.fw = F.matmul(self.L, self.wr)
# calculate backward weighting : bw (N, R)
self.bw = F.matmul(F.transpose(self.L), self.wr)
# calculate read content weighting : cr (N, R)
self.cr_list = [0] * self.R
for i in range(self.R):
self.cr_list[i] = self._C(self.Mem, F.reshape(self.kr[i,:], (1, self.W)), F.reshape(self.beta_r[0,i],(1, 1))) # (N, 1)
self.cr = F.concat(self.cr_list, 1) # (1, N * R)
# compose up-dated read weighting : wr (N, R)
bcf_tensor = F.concat([
F.reshape(F.transpose(self.bw), (self.R, self.N, 1)),
F.reshape(F.transpose(self.cr), (self.R, self.N, 1)),
F.reshape(F.transpose(self.fw), (self.R, self.N, 1))
], 2) # (R, N, 3)
self.pi = F.reshape(self.pi, (self.R, 3, 1)) # (R, 3, 1)
self.wr = F.transpose(F.reshape(F.batch_matmul(bcf_tensor, self.pi), (self.R, self.N))) # (N, R)
def _read_from_memory(self):
# read information from the memory : Mem (N, W) and compose read vector : r (W, R) to reshape (1, W * R)
# read weighting : wr (N, R) must be up-dated before this step
self.r = F.reshape(F.matmul(F.transpose(self.Mem), self.wr), (1, self.R * self.W))
def __call__(self, x):
self._controller_io(x) # input data is processed through the controller
self._up_date_write_weighting()
self._write_to_memory() # memory up-date
self._up_date_read_weighting()
self._read_from_memory() # extract information from the memory
self.y = self.l_Wr(self.r) + self.v # compose total out put y : (1, Y)
return self.y
使用例
使用例も載せますが、DNC (Differentiable Neural Computers) の概要 + Chainer による実装にあるものと内容は同じです。
固定長の one-hot ベクトルをランダムな個数入力し、入力完了後に、出力として入力データを echo させます。echo させたデータと入力データの2乗誤差を loss として、1セットの入力ごとに学習を行います。学習が終了したら、次セットの one-hot ベクトルを入力します。
import dnc
import numpy as np
import chainer
from chainer import functions as F
from chainer import links as L
from chainer import optimizers, Chain, Link, Variable
def onehot(x, n):
ret = np.zeros(n).astype(np.float32)
ret[x] = 1.0
return ret
X = 5
Y = 5
N = 10
W = 10
R = 2
model = dnc.DNC(X, Y, N, W, R)
optimizer = optimizers.Adam()
optimizer.setup(model)
n_data = 10000 # number of input data
loss = 0.0
acc = 0.0
acc_bool = []
for data_cnt in range(n_data):
loss_frac = np.zeros((1, 2))
# prepare one pair of input and target data
# length of input data is randomly set
len_content = np.random.randint(3, 6)
# generate one input data as a sequence of randam integers
content = np.random.randint(0, X-1, len_content)
len_seq = len_content + len_content # the former is for input, the latter for the target
x_seq_list = [float('nan')] * len_seq # input sequence
t_seq_list = [float('nan')] * len_seq # target sequence
for i in range(len_seq):
# convert a format of input data
if (i < len_content):
x_seq_list[i] = onehot(content[i], X)
elif (i == len_content):
x_seq_list[i] = onehot(X-1, X)
else:
x_seq_list[i] = np.zeros(X).astype(np.float32)
# convert a format of output data
if (i >= len_content):
t_seq_list[i] = onehot(content[i - len_content], X)
model.reset_state() # reset reccurent state per input data
# input data is fed as a sequence
for cnt in range(len_seq):
x = Variable(x_seq_list[cnt].reshape(1, X))
if (isinstance(t_seq_list[cnt], np.ndarray)):
t = Variable(t_seq_list[cnt].reshape(1, Y))
else:
t = []
y = model(x)
if (isinstance(t, chainer.Variable)):
loss += (y - t)**2
acc_bool.append(np.argmax(y.data)==np.argmax(t.data))
if (np.argmax(y.data)==np.argmax(t.data)): acc += 1
if (cnt+1==len_seq):
# training by back propagation
model.cleargrads()
loss.grad = np.ones(loss.shape, dtype=np.float32)
loss.backward()
optimizer.update()
loss.unchain_backward()
# print loss and accuracy
if data_cnt < 50 or data_cnt >= 9950:
print('(', data_cnt, ')', acc_bool, ' :: ', loss.data.sum()/loss.data.size/len_content, ' :: ', acc/len_content)
loss_frac += [loss.data.sum()/loss.data.size/len_seq, 1.]
loss = 0.0
acc = 0.0
acc_bool = []
test 結果
10000回繰り返した時の結果です。
[ ]内の bool 値は、出力べクトルで最大値を1に、その他を0に振り直したものが、入力値と一致するかを bool 値で表したものです。
・最初の20回の結果
( 0 ) [True, False, False] :: 0.197543557485 :: 0.3333333333333333
( 1 ) [False, False, False, False] :: 0.209656882286 :: 0.0
( 2 ) [True, False, False] :: 0.172263367971 :: 0.3333333333333333
( 3 ) [False, True, True] :: 0.185363880793 :: 0.6666666666666666
( 4 ) [True, True, True, True] :: 0.157090616226 :: 1.0
( 5 ) [False, False, False, False, False] :: 0.191528530121 :: 0.0
( 6 ) [True, False, False, False, False] :: 0.175649337769 :: 0.2
( 7 ) [False, False, False, True, True] :: 0.173387451172 :: 0.4
( 8 ) [True, False, True, True] :: 0.150813746452 :: 0.75
( 9 ) [False, True, False] :: 0.163899072011 :: 0.3333333333333333
( 10 ) [False, False, False, False, False] :: 0.183468780518 :: 0.0
( 11 ) [True, False, True, False] :: 0.152743542194 :: 0.5
( 12 ) [False, False, True, False] :: 0.170574557781 :: 0.25
( 13 ) [False, True, False, True, False] :: 0.161617393494 :: 0.4
( 14 ) [False, False, False, False] :: 0.168220555782 :: 0.0
( 15 ) [False, False, False] :: 0.167814588547 :: 0.0
( 16 ) [False, True, False, False] :: 0.158575570583 :: 0.25
( 17 ) [False, False, False, False] :: 0.165678012371 :: 0.0
( 18 ) [False, False, False] :: 0.165241924922 :: 0.0
( 19 ) [False, True, False] :: 0.143808253606 :: 0.3333333333333333
・最後20回の結果
( 9980 ) [True, True, True, True] :: 0.000208107382059 :: 1.0
( 9981 ) [True, True, True, True, True] :: 0.000164349582046 :: 1.0
( 9982 ) [True, True, True, True, True] :: 0.000122650777921 :: 1.0
( 9983 ) [True, True, True] :: 0.000181751077374 :: 1.0
( 9984 ) [True, True, True, True, True] :: 0.000318505689502 :: 1.0
( 9985 ) [True, True, True, True, True] :: 0.00023639023304 :: 1.0
( 9986 ) [True, True, True, True, True] :: 0.000988183766603 :: 1.0
( 9987 ) [True, True, True, True, True] :: 0.000226851813495 :: 1.0
( 9988 ) [True, True, True] :: 0.000401457709571 :: 1.0
( 9989 ) [True, True, True, True] :: 0.000256504747085 :: 1.0
( 9990 ) [True, True, True, True, True] :: 0.000165695995092 :: 1.0
( 9991 ) [True, True, True, True] :: 0.000123940082267 :: 1.0
( 9992 ) [True, True, True, True, True] :: 0.000351718552411 :: 1.0
( 9993 ) [True, True, True, True] :: 0.000147357559763 :: 1.0
( 9994 ) [True, True, True, True] :: 0.000173216045368 :: 1.0
( 9995 ) [True, True, True, True] :: 0.000108330522198 :: 1.0
( 9996 ) [True, True, True, True] :: 0.00016659933608 :: 1.0
( 9997 ) [True, True, True] :: 0.000255667418242 :: 1.0
( 9998 ) [True, True, True] :: 0.000280433737983 :: 1.0
( 9999 ) [True, True, True, True, True] :: 0.000443447269499 :: 1.0
完璧に正解しています。20回分しか載せていませんが、最後の100回中でFalseは0回でした。ただし、他の手法と比較まではしていないので、DNC だからこそなのかは不明です。
今回はロジックの紹介が目的だったのでここまでとします。
参考URL
・Chainerの実装例はこのページのものを使わせていただきました
DNC (Differentiable Neural Computers) の概要 + Chainer による実装
・今回はGPU、バッチ処理などは考えてませんでしたが下のページが参考になるかと思います
(Chainer) DNC(Differentiable Neural Computers)で文字列の学習&生成
・Tensor Flowでの実装もあるようです
https://github.com/Mostafa-Samir/DNC-tensorflow
・LSTMの解説はここがわかりやすいです
わかるLSTM ~ 最近の動向と共に