モチベーション
ディープラーニングにあらずんば人工知能にあらずな世の中でも、画像解析や自然言語処理などの非構造データではない、従来通りの構造データに限れば、古きよき機械学習手法はまだまだ手軽かつ高い精度を叩き出す。
例えばサポートベクターマシン、ロジスティック回帰、そしてランダムフォレスト
「でもランダムフォレストってパッケージを使ったことはあるし動作原理もなんとなく知ってるけど、実装したことはないな」
モチベーション完成
ランダムフォレストとは
簡単に言ってしまえば、決定木をたくさん作って多数決によって予測をおこなう手法。
まずは決定木がなんなのかを知らねばならない。
決定木とは
特徴量をひとつ選んでは閾値を決めてデータを分割することを繰り返すことで分類タスクをおこなう学習器。データがどんどん分かれていくさまが木っぽい。
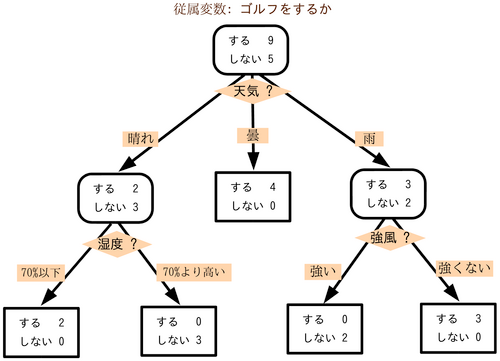
(画像:Wikipedia より)
木を構成する要素にはノードとリンクがある。ノードは各データを閾値によって分割する部分 (上図の黒枠長方形がノード) で、ノードどうしをつなぐのがリンクである。
特に、一番最初のノードを根ノード、それ以上リンクが生えていないノードを葉ノードと呼ぶ。
この記事では各ノードは (葉ノードでない限り) 必ずデータを2分割する2分木だけを取り扱うことにする (上図は3股に分かれるノードがあるので2分木ではない)。
不純度
「各ノードでデータを分割する」とは言っても、基準がなければどうやって分割すればよいのかわからない。その基準となる指標が不純度。
不純度は、「綺麗に分かれているデータは低く、テキトーなデータは高く」なる指標である。
不純度として代表的なものには誤り率や交差エントロピー、ジニ係数などがあるが、今回はジニ係数だけを取り扱う。あるノード $t$ に降ってきたデータにおけるジニ係数の定義は次のとおり:
$$
\mathcal{I}(t) = \sum_{i=1}^K\sum_{j\ne i}P(C_i|t)P(C_j|t) = 1 - \sum_{i=1}^KP^2(C_i|t) = \sum_{i=1}^KP(C_i|t)(1-P(C_i|t))
$$
ただし、$K$ はクラス数、$P(C_i|t)$ はノード $t$ に降ってきたクラス $i$ のデータの割合である。
最後の式の中の $P(C_i|t)(1-P(C_i|t))$ はベルヌーイ分布の分散となっている。ベルヌーイ分布の分散は、投げるコインが偏っているほど小さくなる (コインの同じ面しか出なくなる) ので、最後の式は結局「どれだけ特定のクラスだけに偏っているか」を表している。
ノード $t$ で分割規則を作るときは、不純度の減り方が一番大きな分割を選べば良い。つまり分割を $s$ としたとき、
$$
\Delta\mathcal{I}(s, t) = \mathcal{I}(t) - (p_L\mathcal{I}(t_L) + p_R\mathcal{I}(t_R))
$$
が最大になる $s$ を可能な分割の候補の中から選ぶ。ただし $p_L, p_R$ は $t$ からそれぞれ左側、右側に流れたデータの割合で、$t_L, t_R$ は $t$ から分岐したノードである。不純度の減り方を分割規則で比較するとき、$\mathcal{I}(t)$ はどの分割規則でも同じ値であるから、式全体の値を大きくしたいなら、第二項が一番小さな分割規則を選べば良い。
def _delta_gini_index(self, left, right):
"""ある分割規則によるジニ係数の減少量を計算する (小さいほうがえらい)
left は左側に流れるデータのサンプル (e.g.: [1,1,1,2])
right は右側に流れるデータのサンプル (e.g.: [0,0,0,2,2])
"""
n_left = len(left)
n_right = len(right)
n_total = n_left + n_right
# 左側
_, counts = np.unique(left, return_counts=True) # 各クラスの出現回数を数えて
left_ratio_classes = counts / n_left # 割合にする
left_gain = (n_left / n_total) * (1 - (left_ratio_classes ** 2).sum())
# 右側
_, counts = np.unique(right, return_counts=True) # 各クラスの出現回数を数えて
right_ratio_classes = counts / n_right # 割合にする
right_gain = (n_right / n_total) * (1 - (right_ratio_classes ** 2).sum())
return left_gain + right_gain
木の成長
2分木のノードを表現するクラスをつくる。
class _Node:
"""2分決定木のノード。class_count は必ず持つ。葉ノード以外はそれ以外も持つ。"""
def __init__(self, class_count):
self.class_count = class_count # このノードに属す各クラスのサンプル数
self.feature_id = None # 分割規則に用いたのは「入力Xの何次元目か」のインデックス (int)
self.threshold = None # 分割規則に用いた閾値
self.left = None # このノードの左側のこども。x < threshold
self.right = None # このノードの右側のこども。x >= threshold
@property
def is_leaf(self):
return self.feature_id is None
def __repr__(self):
if self.is_leaf:
return '<Node leaf of class_count: {}>'.format(self.class_count)
else:
return '<Node of class_count: {}, feature_id: {}, threshold: {}>'.format(
self.class_count, self.feature_id, self.threshold)
この _Node をうりうりと連結していけば2分決定木が作れる。分割したあとの左右それぞれのデータに対して再帰的に木を構築すれば良い。
def _grow(self, X, y):
"""(深さ優先で) 再帰的に木を成長させる。メモリ効率は知らん"""
uniques, counts = np.unique(y, return_counts=True) # 各クラスの出現回数を数える (歯抜けあり)
counter = dict(zip(uniques, counts))
class_count = [counter[c] if c in counter else 0 for c in self._classes] # 各クラスの出現回数 (歯抜けなし)
this = _Node(class_count) # まず自分自身を生成
# サンプルがひとつなら葉ノードを返して終了
if len(y) == 1:
return this
# 全部同じクラスなら葉ノードを返して終了
if all(y[0] == y):
return this
# サンプルが全部同じ特徴量をもつ場合は分岐不可能なので葉ノードを返して終了
if (X[0] == X).all():
return this
# この時点で this が葉ノードではなく分岐ノードであることが確定
left_X, left_y, right_X, right_y, feature_id, threshold = self._branch(X, y) # 最適な分割規則を探して、データを分割する
this.feature_id = feature_id
this.threshold = threshold
this.left = self._grow(left_X, left_y) # 左側の木を成長させる
this.right = self._grow(right_X, right_y) # 右側の木を成長させる
return this
決定木のコード
以上を踏まえると、2分決定木のコードは次の通り:
class DecisionTree(ClassifierMixin):
"""2分決定木"""
def __init__(self):
self._tree = None
def fit(self, X, y): # [n_samples, n_features]
self._classes = np.unique(y)
self._tree = self._grow(X, y)
def _grow(self, X, y):
"""(深さ優先で) 再帰的に木を成長させる。メモリ効率は知らん"""
uniques, counts = np.unique(y, return_counts=True) # 各クラスの出現回数を数える (歯抜けあり)
counter = dict(zip(uniques, counts))
class_count = [counter[c] if c in counter else 0 for c in self._classes] # 各クラスの出現回数 (歯抜けなし)
this = _Node(class_count) # まず自分自身を生成
# サンプルがひとつなら葉ノードを返して終了
if len(y) == 1:
return this
# 全部同じクラスなら葉ノードを返して終了
if all(y[0] == y):
return this
# サンプルが全部同じ特徴量をもつ場合は分岐不可能なので葉ノードを返して終了
if (X[0] == X).all():
return this
# この時点で this が葉ノードではなく分岐ノードであることが確定
left_X, left_y, right_X, right_y, feature_id, threshold = self._branch(X, y)
this.feature_id = feature_id
this.threshold = threshold
this.left = self._grow(left_X, left_y) # 左側の木を成長させる
this.right = self._grow(right_X, right_y) # 右側の木を成長させる
return this
def _branch(self, X, y):
"""ジニ係数にしたがってサンプルを分割"""
gains = list() # ジニ係数の減少量の記録 (小さいほうがえらい)
rules = list() # 分岐規則の記録
for feature_id, xs in enumerate(X.transpose()): # 1特徴ずつ調査
thresholds = self._get_branching_threshold(xs) # 分岐の条件となる閾値の候補を全取得
for th in thresholds: # 閾値で分割してみる
left_y = y[xs < th]
right_y = y[th <= xs]
gain = self._delta_gini_index(left_y, right_y) # この分割によるジニ係数の減少量 (小さいほうがえらい)
gains.append(gain)
rules.append((feature_id, th))
best_rule = rules[np.argmin(gains)] # ジニ係数の減少量が一番小さかった規則を採用
feature_id = best_rule[0]
threshold = best_rule[1]
split = X[:, feature_id] < threshold # 閾値による分割を取得
return X[split], y[split], X[~split], y[~split], feature_id, threshold
def _get_branching_threshold(self, xs):
"""xs の分岐の条件となる閾値を全取得"""
unique_xs = np.unique(xs) # np.unique() はソート済みの結果を返すことに注意
return (unique_xs[1:] + unique_xs[:-1]) / 2 # [3, 4, 6] -> [3.5, 5.0]
def _delta_gini_index(self, left, right):
"""ジニ係数の減少量を計算する (小さいほうがえらい)"""
n_left = len(left)
n_right = len(right)
n_total = n_left + n_right
# 左側
_, counts = np.unique(left, return_counts=True) # 各クラスの出現回数を数えて
left_ratio_classes = counts / n_left # 割合にする
left_gain = (n_left / n_total) * (1 - (left_ratio_classes ** 2).sum())
# 右側
_, counts = np.unique(right, return_counts=True) # 各クラスの出現回数を数えて
right_ratio_classes = counts / n_right # 割合にする
right_gain = (n_right / n_total) * (1 - (right_ratio_classes ** 2).sum())
return left_gain + right_gain
def predict(self, X):
proba = self.predict_proba(X)
return self._classes[np.argmax(proba, axis=1)]
def predict_proba(self, X):
if self._tree is None:
raise ValueError('fitしてね')
return np.array([self._predict_one(xs) for xs in X])
def _predict_one(self, xs):
"""1サンプルを予測"""
node = self._tree
while not node.is_leaf: # 葉ノードに到達するまで繰り返す
is_left = xs[node.feature_id] < node.threshold # True: left, False: right
node = node.left if is_left else node.right
class_count = node.class_count
return np.array(class_count) / sum(class_count)
ランダムフォレスト
↑ で作った決定木をたくさん学習させて森にする。このとき、ランダムフォレストの重要なコンセプトがある。各決定木にわたすデータは、元データをブートストラップサンプル (復元ありの抽出) および特徴量をランダムに選択したものである。
def _bootstrap_sample(self, X, y):
"""
与えられたデータをブートストラップサンプル (復元抽出)
同時に、特徴量方向のサンプリングもおこなう。
"""
n_features = X.shape[1]
n_features_forest = np.floor(np.sqrt(n_features))
bootstrapped_X = list()
bootstrapped_y = list()
for i in range(self._n_trees):
ind = np.random.choice(len(y), size=len(y)) # 用いるサンプルをランダムに選択
col = np.random.choice(n_features, size=n_features_forest, replace=False) # 用いる特徴量をランダムに選択
bootstrapped_X.append(X[np.ix_(ind, col)])
bootstrapped_y.append(y[ind])
self._using_features[i] = col
return bootstrapped_X, bootstrapped_y
ランダムフォレストでは、渡すデータをぐちゃまぜにすることでできるだけ各決定木が似たり寄ったりの形にならないように (=多様性を持つように) 工夫している。こうして生成された決定木の多数決によって分類をおこなう。すると、各決定木の持つ多様性のおかげで高い汎化性能を持つようになる。
class RandomForest(ClassifierMixin):
"""↑の2分決定木を使ったランダムフォレスト"""
def __init__(self, n_trees=10):
self._n_trees = n_trees
self._forest = [None] * self._n_trees
self._using_features = [None] * self._n_trees
def fit(self, X, y):
self._classes = np.unique(y)
bootstrapped_X, bootstrapped_y = self._bootstrap_sample(X, y)
for i, (i_bootstrapped_X, i_bootstrapped_y) in enumerate(zip(bootstrapped_X, bootstrapped_y)):
tree = DecisionTree()
tree.fit(i_bootstrapped_X, i_bootstrapped_y)
self._forest[i] = tree
def _bootstrap_sample(self, X, y):
"""
与えられたデータをブートストラップサンプル (復元抽出)
同時に、特徴量方向のサンプリングもおこなう。
"""
n_features = X.shape[1]
n_features_forest = np.floor(np.sqrt(n_features))
bootstrapped_X = list()
bootstrapped_y = list()
for i in range(self._n_trees):
ind = np.random.choice(len(y), size=len(y)) # 用いるサンプルをランダムに選択
col = np.random.choice(n_features, size=n_features_forest, replace=False) # 用いる特徴量をランダムに選択
bootstrapped_X.append(X[np.ix_(ind, col)])
bootstrapped_y.append(y[ind])
self._using_features[i] = col
return bootstrapped_X, bootstrapped_y
def predict(self, X):
proba = self.predict_proba(X)
return self._classes[np.argmax(proba, axis=1)]
def predict_proba(self, X):
if self._forest[0] is None:
raise ValueError('fitしてね')
votes = [tree.predict(X[:, using_feature]) for tree, using_feature in zip(self._forest, self._using_features)] # n_trees x n_samples
counts = [Counter(row) for row in np.array(votes).transpose()] # n_samples だけの Counter オブジェクト
# 各 tree の意見の集計
counts_array = np.zeros((len(X), len(self._classes))) # n_samples x n_classes
for row_index, count in enumerate(counts):
for class_index, class_ in enumerate(self._classes):
counts_array[row_index, class_index] = count[class_]
proba = counts_array / self._n_trees # 規格化する
return proba
性能
今まで断片的に書いていたコードの全体は次の通り。決定木およびランダムフォレストのクラスに ClassifierMixin を継承させているが、これは score という精度測定のメソッドが追加されるだけ (Scikit-learn のクラスタリング手法は必ず ClassifierMixin を継承している)。
# coding=utf-8
import logging
from collections import Counter
import numpy as np
from sklearn.base import ClassifierMixin
class _Node:
"""2分決定木のノード。class_count は必ず持つ。葉ノード以外はそれ以外も持つ。"""
def __init__(self, class_count):
self.class_count = class_count # このノードに属す各クラスのサンプル数
self.feature_id = None # 分割規則に用いたのは「入力Xの何次元目か」のインデックス (int)
self.threshold = None # 分割規則に用いた閾値
self.left = None # このノードの左側のこども。x < threshold
self.right = None # このノードの右側のこども。x >= threshold
@property
def is_leaf(self):
return self.feature_id is None
def __repr__(self):
if self.is_leaf:
return '<Node leaf of class_count: {}>'.format(self.class_count)
else:
return '<Node of class_count: {}, feature_id: {}, threshold: {}>'.format(
self.class_count, self.feature_id, self.threshold)
class DecisionTree(ClassifierMixin):
"""2分決定木"""
def __init__(self):
self._tree = None
def fit(self, X, y): # [n_samples, n_features]
self._classes = np.unique(y)
self._tree = self._grow(X, y)
def _grow(self, X, y):
"""(深さ優先で) 再帰的に木を成長させる。メモリ効率は知らん"""
uniques, counts = np.unique(y, return_counts=True) # 各クラスの出現回数を数える (歯抜けあり)
counter = dict(zip(uniques, counts))
class_count = [counter[c] if c in counter else 0 for c in self._classes] # 各クラスの出現回数 (歯抜けなし)
this = _Node(class_count) # まず自分自身を生成
# サンプルがひとつなら葉ノードを返して終了
if len(y) == 1:
return this
# 全部同じクラスなら葉ノードを返して終了
if all(y[0] == y):
return this
# サンプルが全部同じ特徴量をもつ場合は分岐不可能なので葉ノードを返して終了
if (X[0] == X).all():
return this
# この時点で this が葉ノードではなく分岐ノードであることが確定
left_X, left_y, right_X, right_y, feature_id, threshold = self._branch(X, y)
this.feature_id = feature_id
this.threshold = threshold
this.left = self._grow(left_X, left_y) # 左側の木を成長させる
this.right = self._grow(right_X, right_y) # 右側の木を成長させる
return this
def _branch(self, X, y):
"""ジニ係数にしたがってサンプルを分割"""
gains = list() # ジニ係数の減少量の記録 (小さいほうがえらい)
rules = list() # 分岐規則の記録
for feature_id, xs in enumerate(X.transpose()): # 1特徴ずつ調査
thresholds = self._get_branching_threshold(xs) # 分岐の条件となる閾値の候補を全取得
for th in thresholds: # 閾値で分割してみる
left_y = y[xs < th]
right_y = y[th <= xs]
gain = self._delta_gini_index(left_y, right_y) # この分割によるジニ係数の減少量 (小さいほうがえらい)
gains.append(gain)
rules.append((feature_id, th))
best_rule = rules[np.argmin(gains)] # ジニ係数の減少量が一番小さかった規則を採用
feature_id = best_rule[0]
threshold = best_rule[1]
split = X[:, feature_id] < threshold # 閾値による分割を取得
return X[split], y[split], X[~split], y[~split], feature_id, threshold
def _get_branching_threshold(self, xs):
"""xs の分岐の条件となる閾値を全取得"""
unique_xs = np.unique(xs) # np.unique() はソート済みの結果を返すことに注意
return (unique_xs[1:] + unique_xs[:-1]) / 2 # [3, 4, 6] -> [3.5, 5.0]
def _delta_gini_index(self, left, right):
"""ジニ係数の減少量を計算する (小さいほうがえらい)"""
n_left = len(left)
n_right = len(right)
n_total = n_left + n_right
# 左側
_, counts = np.unique(left, return_counts=True) # 各クラスの出現回数を数えて
left_ratio_classes = counts / n_left # 割合にする
left_gain = (n_left / n_total) * (1 - (left_ratio_classes ** 2).sum())
# 右側
_, counts = np.unique(right, return_counts=True) # 各クラスの出現回数を数えて
right_ratio_classes = counts / n_right # 割合にする
right_gain = (n_right / n_total) * (1 - (right_ratio_classes ** 2).sum())
return left_gain + right_gain
def predict(self, X):
proba = self.predict_proba(X)
return self._classes[np.argmax(proba, axis=1)]
def predict_proba(self, X):
if self._tree is None:
raise ValueError('fitしてね')
return np.array([self._predict_one(xs) for xs in X])
def _predict_one(self, xs):
"""1サンプルを予測"""
node = self._tree
while not node.is_leaf: # 葉ノードに到達するまで繰り返す
is_left = xs[node.feature_id] < node.threshold # True: left, False: right
node = node.left if is_left else node.right
class_count = node.class_count
return np.array(class_count) / sum(class_count)
class RandomForest(ClassifierMixin):
"""↑の2分決定木を使ったランダムフォレスト"""
def __init__(self, n_trees=10):
self._n_trees = n_trees
self._forest = [None] * self._n_trees
self._using_features = [None] * self._n_trees
def fit(self, X, y):
self._classes = np.unique(y)
bootstrapped_X, bootstrapped_y = self._bootstrap_sample(X, y)
for i, (i_bootstrapped_X, i_bootstrapped_y) in enumerate(zip(bootstrapped_X, bootstrapped_y)):
tree = DecisionTree()
tree.fit(i_bootstrapped_X, i_bootstrapped_y)
self._forest[i] = tree
def _bootstrap_sample(self, X, y):
"""
与えられたデータをブートストラップサンプル (復元抽出)
同時に、特徴量方向のサンプリングもおこなう。
"""
n_features = X.shape[1]
n_features_forest = np.floor(np.sqrt(n_features))
bootstrapped_X = list()
bootstrapped_y = list()
for i in range(self._n_trees):
ind = np.random.choice(len(y), size=len(y)) # 用いるサンプルをランダムに選択
col = np.random.choice(n_features, size=n_features_forest, replace=False) # 用いる特徴量をランダムに選択
bootstrapped_X.append(X[np.ix_(ind, col)])
bootstrapped_y.append(y[ind])
self._using_features[i] = col
return bootstrapped_X, bootstrapped_y
def predict(self, X):
proba = self.predict_proba(X)
return self._classes[np.argmax(proba, axis=1)]
def predict_proba(self, X):
if self._forest[0] is None:
raise ValueError('fitしてね')
votes = [tree.predict(X[:, using_feature]) for tree, using_feature in zip(self._forest, self._using_features)] # n_trees x n_samples
counts = [Counter(row) for row in np.array(votes).transpose()] # n_samples だけの Counter オブジェクト
# 各 tree の意見の集計
counts_array = np.zeros((len(X), len(self._classes))) # n_samples x n_classes
for row_index, count in enumerate(counts):
for class_index, class_ in enumerate(self._classes):
counts_array[row_index, class_index] = count[class_]
proba = counts_array / self._n_trees # 規格化する
return proba
if __name__ == '__main__':
from sklearn import datasets
from sklearn.cross_validation import train_test_split
from sklearn.ensemble import RandomForestClassifier
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
dt = DecisionTree()
dt.fit(X_train, y_train)
rf = RandomForest()
rf.fit(X_train, y_train)
print('DecisionTree: ')
# dt_predicted_y_train = dt.predict(X_train)
# print(' predicted_y_train: {}'.format(dt_predicted_y_train))
# print(' (actual) : {}'.format(y_train))
print(' score_train: {}'.format(dt.score(X_train, y_train)))
# dt_predicted_y_test = dt.predict(X_test)
# print(' predicted_y_test: {}'.format(dt_predicted_y_test))
# print(' (actual) : {}'.format(y_test))
print(' score_test: {}'.format(dt.score(X_test, y_test)))
print('RandomForest: ')
# rf_predicted_y_train = rf.predict(X_train)
# print(' predicted_y_train: {}'.format(rf_predicted_y_train))
# print(' (actual) : {}'.format(y_train))
print(' score_train: {}'.format(rf.score(X_train, y_train)))
# rf_predicted_y_test = rf.predict(X_test)
# print(' predicted_y_test: {}'.format(rf_predicted_y_test))
# print(' (actual) : {}'.format(y_test))
print(' score_test: {}'.format(rf.score(X_test, y_test)))
print('Scikit-learn RandomForest: ')
ret = RandomForestClassifier().fit(X_train, y_train)
print(' score_train: {}'.format(ret.score(X_train, y_train)))
print(' score_test: {}'.format(ret.score(X_test, y_test)))
実行してみる ($ python randomforest.py) と、次のような結果が得られた:
$ python randomforest.py
DecisionTree:
score_train: 1.0
score_test: 0.96
RandomForest:
score_train: 0.98
score_test: 0.98
Scikit-learn RandomForest:
score_train: 1.0
score_test: 0.98
今回は決定木の枝刈り剪定は一切おこなっていないため、DecisionTree の学習スコア (score_train) は1となる。テストスコア (score_test、汎化性能) では RandomForest のほうが良い値となっている。
結論
Scikit-learn を使おう
参考文献
- はじめてのパターン認識 (森北出版、平井有三 著 2012)
- Scikit-learn (RandomForest, DecisionTree, ClassifierMixin)
- [NumPy] (http://www.numpy.org/)



