NTTドコモ クロステック開発部の小松です。
この記事はNTTドコモ R&D 控え室 Advent Calendar 2020の18日目の記事です。
はじめに
最近、音楽制作を趣味で始めたのですが、同時に「データサイエンス関連の技術を用いて音楽作成ができないだろうか?」と音楽の生成の分野に興味を持ち始めました。
今回は簡易な方法としてマルコフ連鎖という確率モデルを用いてメロディーを生成に取り組んだ内容を紹介させていただきます。
🔰機械学習や音楽分野に関する初学者です。
必要なもの
- Python 3.7.3(諸々のライブラリ)
- PC(自分はMacbookのmacOS Catalina ver.10.15.5)
- 音楽編集ソフト(筆者はMacの中にあったGarageBandを使っています)
- Midiデータで作られたメロディー
音楽について(DTM〜MIDI)
DTMとは何か
今回の記事ではDTM(Desk Top Musicの略)という、その名の通り、パソコン上で音楽作成や編集をすることについて扱います。
「楽器が弾けなくても、パソコン上で音楽が作れる」という点が筆者にとっては利点だと思います。
DTMに必要なもの
今回の記事のように、プログラムで音楽生成する場合は音楽編集が可能なPC、音楽編集ソフトDAW(Digital Audio Workstation)があれば音楽を作ることはできます。(音楽制作をしている知人曰く、1から人の手で音楽を制作する場合、効率のことを考えると楽器も必要になってくる様です…)
DAWソフト
このDAWソフトについて代表的なものとして、アップル製品であれば、Logic Pro Xだったり、Garage Bandというものがあり、知っている方も多のではないかと思います。その他有料のものからフリーのDAWソフト等ありますが、今回はDAWソフトには簡単に3つの機能があるということだけ覚えていただけると良いのかなと思います。
- マルチトラック録音(複数の楽器を別々に録音して最後にまとめられる)
- 打ち込み(どんな音をどんなタイミング、長さで鳴らすか入力する)
- ミックス(複数の音同士のバランス調整)
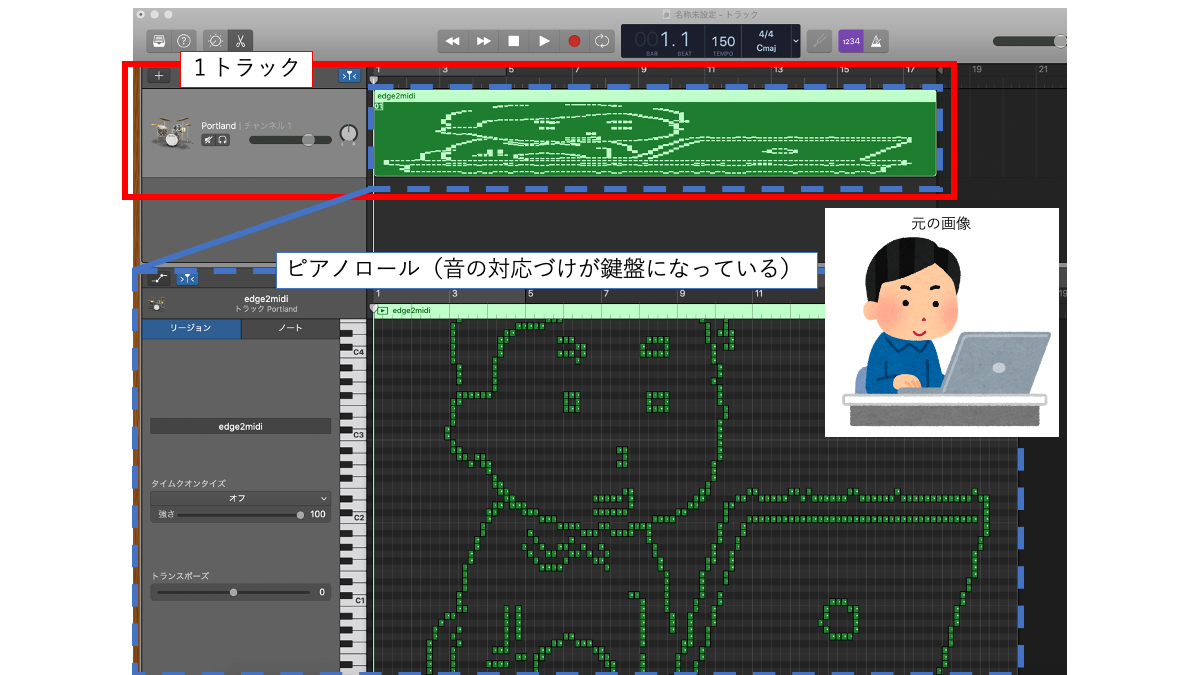
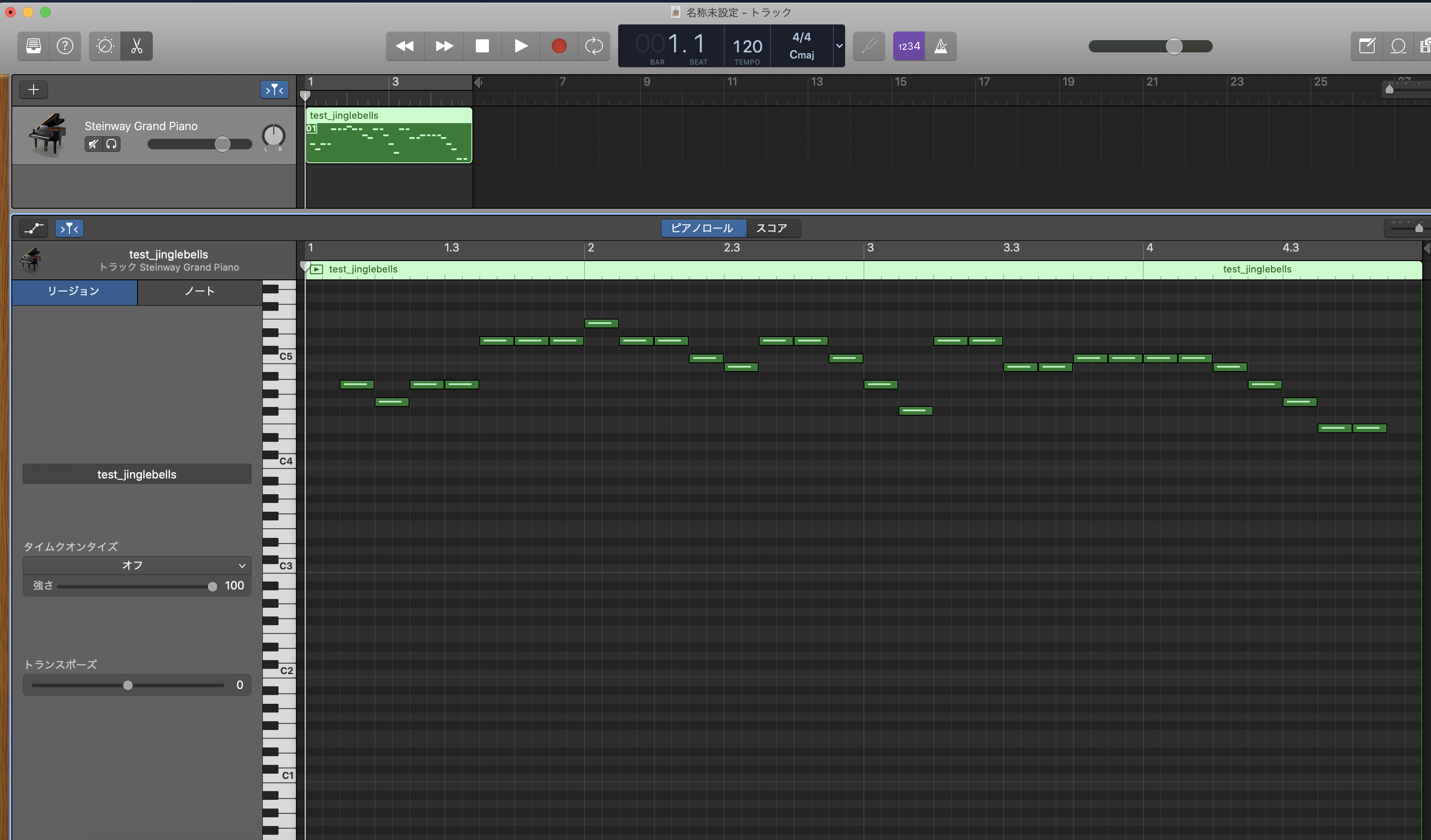
(以下、GarageBandのUI画面)
例として画像のエッジを検出して音楽を生成してみました。
この内容は過去のQiitaにも載っていたので、説明は割愛します。音声の波形データやこの時系列的な鍵盤情報のまとまり(=トラック)を複数集めることによって、複雑な音楽を作成することもできます。
MIDIとは
音楽データについて、今回はMIDIという聞き慣れないものについて簡単に説明します。
MIDI(読み方はミディ、Musical Instrument Digital Interfaceの略)は電子楽器の演奏データを機器の間で転送共有する共通規格(General MIDIに基づく)のことを表しています。MIDIファイルは後から編集が可能で、修正や変更がしやすいのが特徴であることから、音楽制作の場で多く活用されています。
拡張子は.midが標準です。
General MIDI の楽器コード
そんな共有規格のGMですが、128種類の楽器や効果音が数字のリストとして規定されています。詳細リストについては、こちらのURLを参照してみてください。
例)ピアノの音色
| 番号 | 種類 |
|---|---|
| 1 | Acoustic Grand Piano |
| 2 | Bright Acoustic Piano |
| 3 | Electric Grand Piano |
| ... | ... |
ピアノなどの各系統に8種類ずつ音色が登録されています。
フリーのMIDIデータについて
今回は、著作権が切れている曲をまとているサイトからクリスマス間近という事で、「ジングルベル」のMIDIファイルをダウンロードして使用しました。
技術的な部分(概要〜実装)
マルコフ連鎖について(概要)
今回の記事では離散時間マルコフ連鎖を活用します。その大まかな概要について確認するために以下、Wikiの概要を確認してみましょう。
マルコフ連鎖(マルコフれんさ、英: Markov chain)とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的(有限または可算)なもの(離散状態マルコフ過程)をいう。また特に、時間が離散的なもの(時刻は添え字で表される)を指すことが多い(他に連続時間マルコフ過程というものもあり、これは時刻が連続である)。マルコフ連鎖は、未来の挙動が現在の値だけで決定され、過去の挙動と無関係である(マルコフ性)。各時刻において起こる状態変化(遷移または推移)に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。特に重要な確率過程として、様々な分野に応用される。
マルコフ連鎖に関するWikiだけで理解するのがやや苦しかったので、
「確率変数」→「確率過程」→「マルコフ性」→「マルコフ過程」→「マルコフ連鎖」
の順番で調べて、筆者なりに意味を確認し要約したものを以下に示します。
確率変数(かくりつへんすう、英:)
ある値や状態となる確率が存在する変数のことを表している。結果の状態や値のこと。
例)サイコロの出目{1,2,3,4,5,6}の1の目
確率過程(かくりつかてい、英:stochastic process)
時間とともに変化する確率変数のこと。
例)サイコロを転がした回数と結果の集合。
マルコフ性(マルコフせい、英: Markov property)
確率過程において、未来の状態が、現在の状態のみに依存し、過去のいかなる状態にも依存しない特性。
マルコフ過程(マルコフかてい、英: Markov process)
マルコフ性を持つ確率過程のことを表している。
マルコフ連鎖(マルコフかてい、英: Markov chain)
マルコフ過程のうち、取りうる状態が離散的(天気、サイコロ、トランプなど)なもの。離散時間マルコフ連鎖を指す(りさんじかんマルコフれんさ、英:Discrete-time Markov Chains)
これら5つのことから、マルコフ連鎖というのは、「未来の状態が現在の状態のみで決まるという条件の中」で、「天気などの離散的な状態があったときに」、「現在の状態から未来の状態に遷移する際の確率を表現するもの」と簡単に覚えておきたいと思います。
数式
上記説明に従って、マルコフ連鎖の数式を作成します。確率過程を$(X_0,X_1,...,X_n)$とすると、未来の値$X_{n+1}$の状態は$X_n$にのみ依存するので、
$P(X_j|(X_0,X_1,.,X_i,X_j,...,X_n))=P(X_j|X_i)$
となります。
例)天気予報
$X_t$ がとりうる値の集合のことを状態空間と言うことがあります。例えば,天気の例だと状態空間は$ S$={晴れ,曇,雨} と考えることができます。晴れ,曇,雨の各状態をそれぞれ 1,2,3 で表すと便利です。このとき $S$={1,2,3} と書けます。また,$P(X_{t+1}∣X_t) $のことを遷移確率(推移確率)と言うことがあります。例えば「今日曇りだと確率 0.3 で明日晴れになる」場合,遷移確率は $P(X_{t+1}$=晴れ$∣X_t$=曇)=0.3 となります。
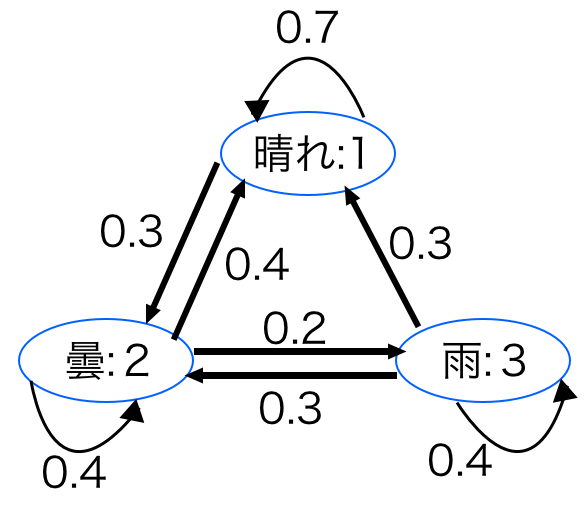
引用元の遷移確率を表した状態遷移図と引用文の内容に相関はなさそうで、少し混乱しましたが、この図の内容について解釈したものと、上の遷移図に関する対応表(遷移行列)を作りました。
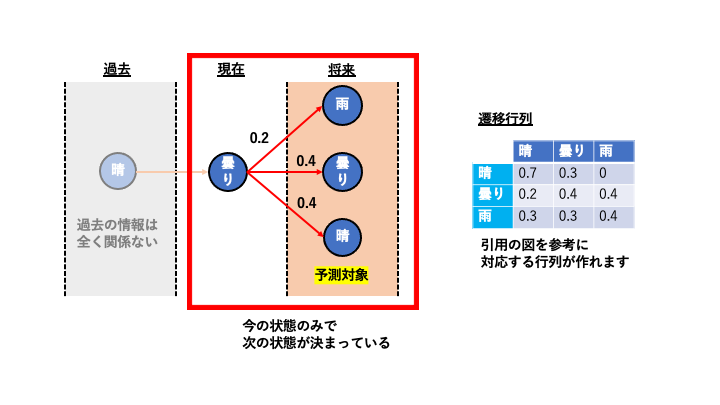
N-gram マルコフモデル
今回の音楽生成について、実装の際に参考にしたプログラムのコメントにbi-gramという言葉が出てきます。これは自然言語処理に用いられる「N-gram」を用いているようで、n個の連続する記号の頻度を集計することを指します。この「N-gram」をマルコフモデルに応用する事で、n-1の連続する記号からn番目の記号を推定することができます。より詳細な内容は下記の引用でわかりやすくまとめられています。
「N-gram」とは,自然言語処理分野で用いられる手法の1つである.N-gramでは対象となる文書を文字単位の記号列と考え,隣接したN個の記号毎の出現頻度(度数と呼ぶ)を集計する.
隣接した1個の記号からなる記号列(つまり,1文字)毎の度数をuni-gram,2個の記号をbi-gram,3個の記号ならをtri-gram,…と呼ぶ.(中略)
N-gramを使用した場合,文法情報を用いずに文書を分解できるため,言語に依存しない文書の分割が可能となる.また,言語学的に意味を持たない記号列についても集計が可能なため,テキスト処理を含む自然言語処理分野では多く用いられている.
(引用元:https://mieruca-ai.com/ai/bi-gram_markov_model/)
ここで筆者は思いました。『「bi-gramマルコフモデル」の考え方とさっき説明していたマルコフ連鎖って似てない?』
その通りでした。bi-gramマルコフモデルは先ほど説明したマルコフ連鎖と同じことを実施しています。
実装編
ここからは実際に、前述した著作権フリーのMIDIデータからメロディー部分を抽出し、マルコフ連鎖を活用する方法について紹介していきます。
pretty_midi
MIDIデータをプログラム的に編集、処理することができるものの1つとして、pythonライブラリのpretty_midiがあります。今回は過去のQiitaの記事を参考にインストールしています。
インストール方法
git clone https://github.com/craffel/pretty-midi
cd pretty-midi
python setup.py install
MIDIファイル内部に登録されいてる情報について
import pretty_midi
# PrettyMIDIで.midiを読み込む
midi_data = pretty_midi.PrettyMIDI('jinglebells.mid')
# トラックリストを表示する
print(midi_data.instruments)
実行結果
[Instrument(program=82, is_drum=False, name="Melody "),
Instrument(program=38, is_drum=False, name="Bass "),
Instrument(program=16, is_drum=False, name="Chord "),
Instrument(program=88, is_drum=False, name="Synth "),
Instrument(program=89, is_drum=False, name="Pad "),
Instrument(program=0, is_drum=True, name="Drums ")]
Instrumentsメソッドには、以下の情報が入っています。
-
GMコードの音色(Program)
-
ドラムかどうか(is_drum)
-
トラックの名前(name)
このジングルベルのメロディートラックを抽出し、中のデータを確認します。
# メロディ部分を抽出し確認する
melody=midi_data.instruments[0]
print(melody.notes)
実行結果
[Note(start=3.692304, end=3.903842, pitch=74, velocity=100), Note(start=3.923073, end=4.134611, pitch=83, velocity=95), Note(start=4.153842, end=4.365380, pitch=81, velocity=100),.....
このNoteには以下の弾き方の情報が入っています。
-
どのタイミング(start)で
-
どの鍵盤(Pitch)を
-
どのくらいの強さで(velocity)で叩くのか
この結果から、MIDIデータを1つずつのブロックとして離散的に情報が登録されていると仮定できるのではないかと思います。実際のところ、音自体は連続のアナログ信号と捉えることができるので、そうとはいえないかもしれないですが、マルコフ連鎖によって音楽を作成できるのではないかということで筆者も納得しました。
マルコフ連鎖の実装
今回は、Markov Chain for music generationという記事を参考にGithubにアップロードされているコードを活用しました。Githubに上げられている例としては実際の音楽のコード列(F,Em7など)からマルコフ連鎖を用いて音楽を生成するモデルになっていますが、これを筆者が取り扱いたい、Pretty _MIDIの鍵盤情報から音楽を生成するモデルにしてみました。
各種ライブラリとMIDIデータの読込
import pretty_midi
import numpy as np
import pandas as pd
from collections import Counter
np.random.seed(42)
# Load MIDI file into PrettyMIDI object
midi_data = pretty_midi.PrettyMIDI('jinglebells.mid')
Bi-gram(n=2)の生成
# メロディ部分を抽出する
melody=midi_data.instruments[0]
# print(melody.notes)
# ノート内のピッチを格納する※GithubではCSVファイルを取り込むようになっているのでピッチから読み込めるようにする
pitches=[]
for note in melody.notes:
pitches.append(str(note.pitch))
n = 2
ngrams = zip(*[pitches[i:] for i in range(n)])
bigrams = [" ".join(ngram) for ngram in ngrams]
print(bigrams[:5])
マルコフ連鎖によって次の状態を予測するモデル
# 現在のピッチから、次のピッチを予測
def predict_next_state(pitch:str, data:list=bigrams):
# 現在のピッチからとりうる次のピッチとなるバイグラムのリストを作成する
bigrams_with_current_pitch = [bigram for bigram in bigrams if bigram.split(' ')[0]==pitch]
# 現れたバイグラムの数を数える
count_appearance = dict(Counter(bigrams_with_current_pitch))
# 確率に変換する
for ngram in count_appearance.keys():
count_appearance[ngram] = count_appearance[ngram]/len(bigrams_with_current_pitch)
# 確率と紐づいたピッチリストを生成
options = [key.split(' ')[1] for key in count_appearance.keys()]
# ピッチに対応した確率のリストを生成
probabilities = list(count_appearance.values())
# 候補となるピッチを生成する
return np.random.choice(options, p=probabilities)
連鎖式に30個先までのピッチリストを作成する
def generate_sequence(pitch:str=None, data:list=bigrams, length:int=30):
"""Generate sequence of defined length."""
# 30個のピッチリストを作成する
pitches = []
for n in range(length):
# 予測結果を追加しリスト更新
pitches.append(predict_next_state(pitch, bigrams))
# 予測したピッチを入力に変更
pitch = pitches[-1]
return pitches
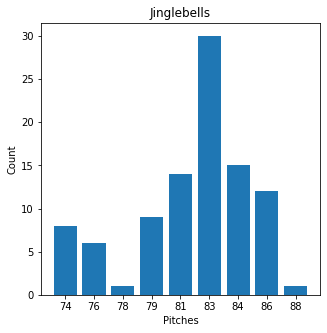
またジングルベルのメロディーについて、ピッチのヒストグラム を取った結果、83が最も多く得られました。
この83のピッチを基本としたメロディーなのだろうということがわかります。
生成した30個のリストをもとに、音楽を生成する
# 連続したピッチを生成する
new_melody=generate_sequence('83')
length=len(new_melody)
# Pretty_MIDIにデータを入力
pm = pretty_midi.PrettyMIDI()
# 楽器の種類を選択する。General MIDI instruments codeに従う。1: Acoustic Grand Piano
instrument = pretty_midi.Instrument(1)
# カウント
cnt=1
# Noteに情報を格納
for i in new_melody:
note = pretty_midi.Note(velocity=100, pitch=int(i), start=cnt*0.25, end=cnt*0.25+0.25)
cnt+=1
instrument.notes.append(note)
# トラック作成
pm.instruments.append(instrument)
# 書き込み
pm.write('test_jinglebells.mid')
結果
出力された音楽データは次の通りです。
ジングルベルのメロディーを活用して、新しくメロディーを生成することができました。
この生成されたメロディーについて、何度かジングルベルと聴き比べてみましたが、若干似ている部分があるな?と筆者は感じました。皆さんはいかがでしょうか?
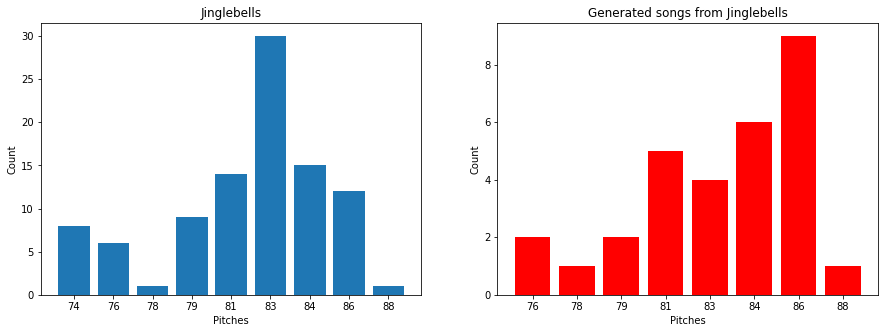
また、ジングルベルと、生成された結果についてお互いにヒストグラム をとってみました。生成したメロディーでも元のジングルベルで頻度が多い、81~86のピッチ部分が多く使われていることが確認できました。
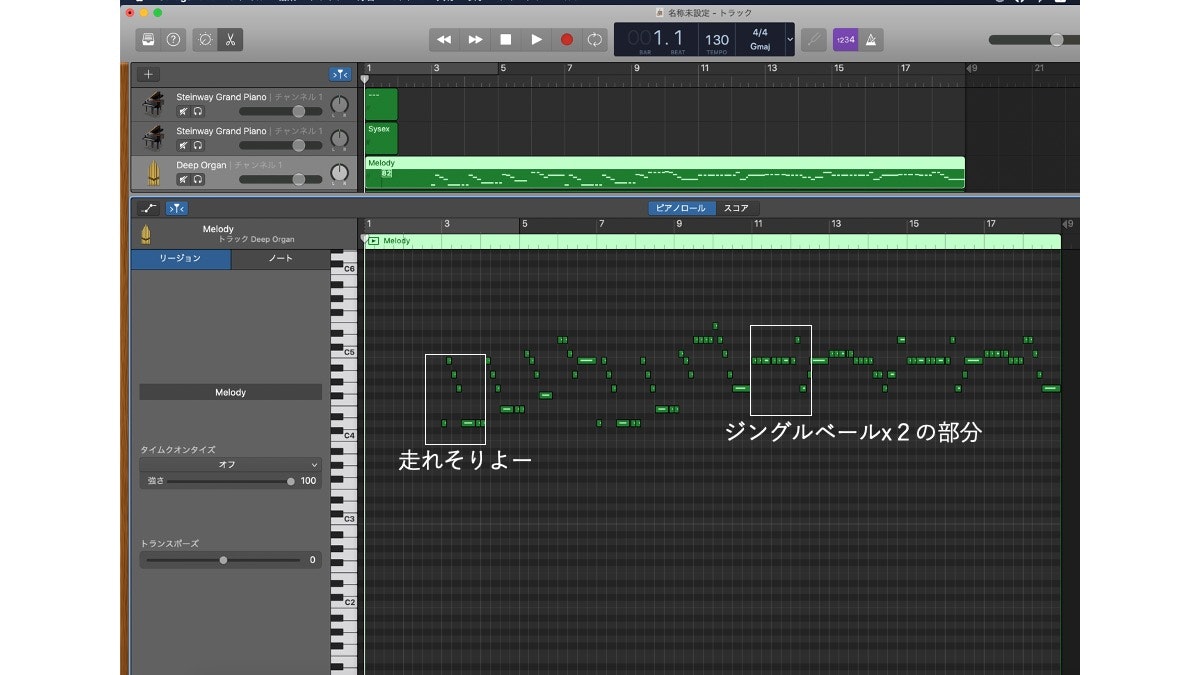
元のデータのジングルベルについては以下のピアノロールを確認いただければと思います。
余談ですが、筆者はキャッチーな曲を聞くと数週間くらい頭から離れなってしまうタイプで、気づいた頃にはジングルベルが頭の中で流れてくるようになっちゃいました。(記:11月末…)
今回の投稿では生成された音楽の段階で鍵盤情報のみの抽出となっていることから、どのくらいの長さでかつ、どのくらいの強さで音を鳴らすかと言ったような情報が消えてしまいました。
今回は時間制約的に難しいですが、対策はできるかもしれないなと思っていますので、一案を簡単にご紹介します。
その方法として検討しているのは**「長さ、強さもピッチと切り離して離散的マルコフ連鎖を活用する」**です。
MIDIデータのNote部分はこのような構成となっています。
Note(start=3.692304, end=3.903842, pitch=74, velocity=100)
このStartとendの差、Velocityそれぞれの時系列的なリストを作成することで、今回と同様の方法で生成可能と考えます。
おわりに
今回は入力された音楽のメロディーパートからマルコフ連鎖を用いて、連鎖式に決められた長さの音楽を再生する方法をご紹介しました。
少なくともPython上でデータサイエンス分野でも活用されている技術を使ってMIDIデータを作成することができた筆者としては今回の結果にかなり満足しています。
筆者も業務では今後時系列のデータを扱うこともあり、趣味を通してマルコフ過程の1つとしてマルコフ連鎖を学習するとっても良い機会になりました。機械学習による音楽生成としてはGoogleのオープンソフトウェアのMagentaプロジェクトが有名ですが、今後活用も検討してみたいなと思います。以上です!