はじめに

この記事は、数学 Advent Calendar 2015 22日目の記事です。
なお私は、物理学を専門としていまして、数学や数値計算は自分の研究に必要な部分を多少かじったことがあるぐらいですので、以下のアルゴリズムの数学的な厳密性についての議論はよく分かりませんが、ご容赦願います。

1次元関数の最小化とは

数値計算では、しばしば1次元関数$f\left( x\right)$を最小化せよ、という問題に出くわします。具体的には、ある実関数$f\left( x\right)$が与えられたとき、

m=\min\limits_{x\in R}f\left(  x\right)

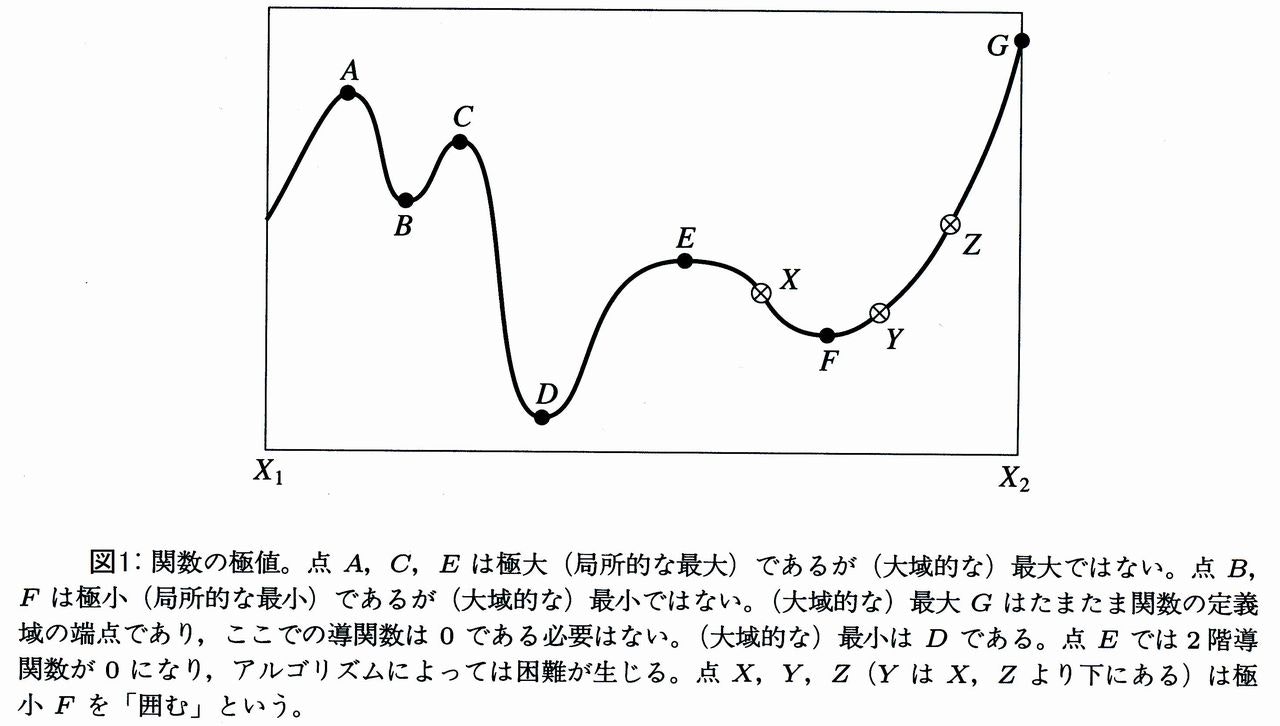
上式の$m$およびその時の$x$を求めよという問題です。しかし残念ながら、大域的な最小値（global minimum）を、確実に求める数値的アルゴリズムは、ほとんど知られていません。以下で説明するアルゴリズムで求められるのは、大抵、局所的な最小値（local minimum）です。また、local minimumが求まるか、あるいはglobal minimumが求まるかは、与えた区間にも依存します。
この様子は、以下の図1を見ていただければ分かりやすいかと思います（図は参考文献[1]より引用）。

黄金分割法

Brentの方法を説明する前にまず、より簡単なアルゴリズムである黄金分割法を、以下の図を用いて簡単に説明します（図は参考文献[1]より引用）。

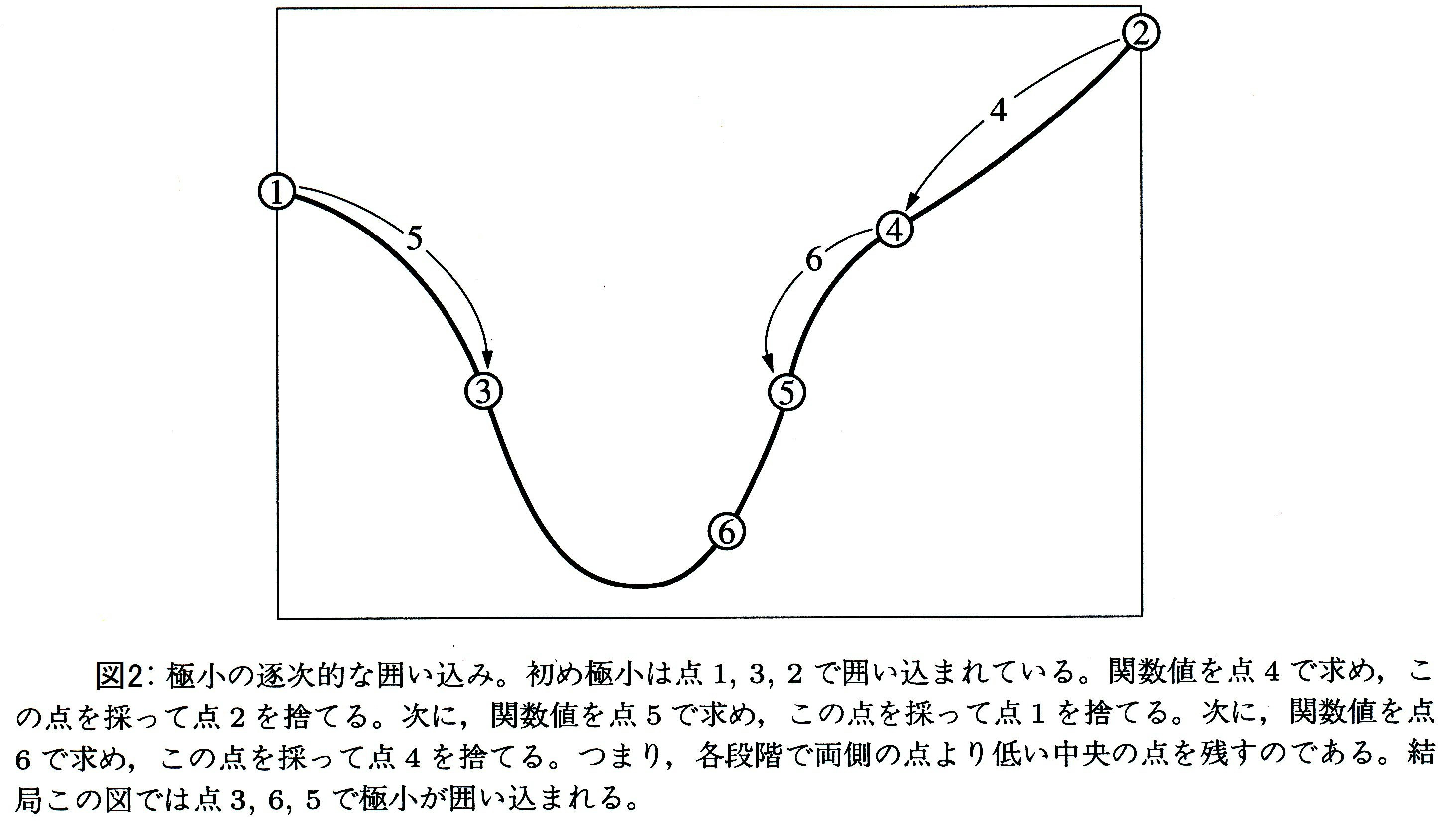
まず最初に、図のように、点①、点②、点③で関数$f\left( x\right)$の値が評価されているとします。ただし、$①<③<②$であり、区間[①,②]で関数$f\left( x\right)$は単峰関数であるとします。図から、$f\left( ③\right)<f\left( ①\right)<f\left( ②\right)$であるので、$f\left( x\right)$は区間[①,②]に必ず最小値を有することが分かります。
次のステップでは、新しい点④で関数を評価し、関数形を探ります。図から、$f\left( ③\right)<f\left( ④\right)$ですので、$f\left( x\right)$は区間[①,④]に必ず最小値を有することが分かります（逆に、$f\left( ④\right)<f\left( ③\right)$だったならば、$f\left( x\right)$は区間[③,②]に必ず最小値を有することになります）。そして同様のことを、区間幅が十分小さくなるまで繰り返します。
しかし、区間[①,②]が与えられたとき、点③は①と②の間の一体どこを取れば良いのでしょうか。詳しい解説は参考文献[1]に譲りますが、点③は区間[①,②]を、

\dfrac{3-\sqrt{5}}{2}:\dfrac{\sqrt{5}-1}{2}\simeq0.38197:0.61803

と分割するように選べば良い、と言うことが分かっています。

逆放物線補間とBrentの方法

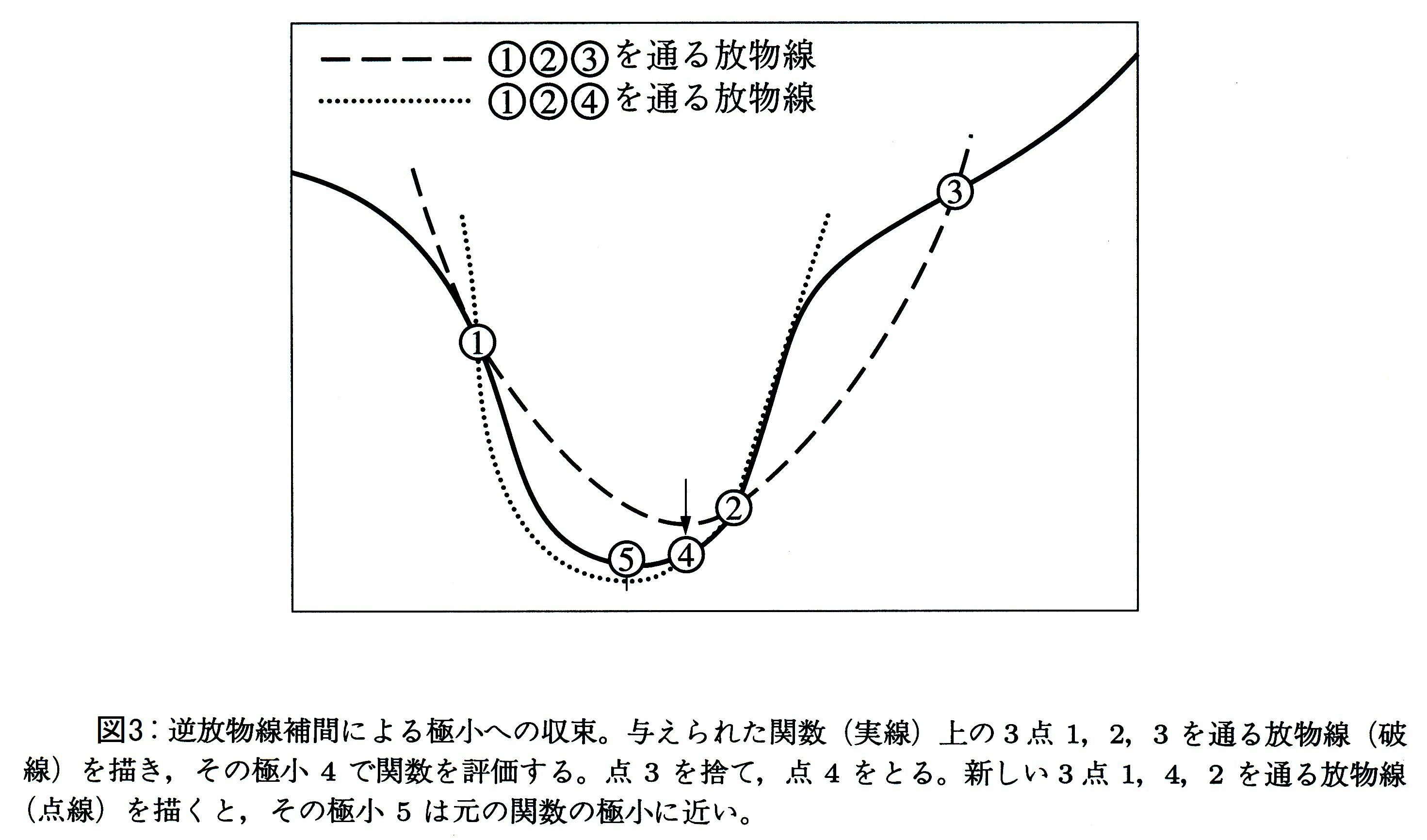
黄金分割法による関数の最小化は、関数$f\left( x\right)$が非協力的な場合に有用な方法であり、確実に最小を追い詰めていきます。しかし、なぜ関数が非協力的な場合だけを考えるのでしょうか。もし、関数$f\left( x\right)$が協力的で素直な場合、関数は最小値の近くで放物線で近似できると考えられます。従って、図3のように、任意の3点に放物線を当てはめれば、最小値を与える点の非常に近いところに効率よく到達できるはずです（図は参考文献[1]より引用）。

この方法は、逆放物線補間（逆2次補間）と呼ばれます。3点$f\left( a\right), f\left( b\right), f\left( c\right)$を通る放物線の最小値のx座標を求める公式は、

x=b-\dfrac{1}{2}\dfrac{\left(  b-a\right)  ^{2}\left[  f\left(  b\right)
-f\left(  c\right)  \right]  -\left(  b-c\right)  ^{2}\left[  f\left(
b\right)  -f\left(  a\right)  \right]  }{\left(  b-a\right)  \left[  f\left(
b\right)  -f\left(  c\right)  \right]  -\left(  b-c\right)  \left[  f\left(
b\right)  -f\left(  a\right)  \right]  }

となります。しかし、3点が1直線上にある場合、この公式は分母が0になるので用いることができません。また、この公式が放物線の最大を与える可能性もあります。従って、この公式だけに頼ることはできません。
そこで、関数が非協力的なときは黄金分割法のような遅いが確実な方法に頼り、そうでないときは逆放物線補間に切り替えるような方法が最も好ましいと考えられます。といっても、これは結構厄介な問題です。なぜなら、

二つの方法の切り替えを行う際に無駄な関数評価を省くための段取りが大変
終盤の丸め誤差の限界近くでの計算に注意が必要
関数が協力的か非協力的かを調べる方法は十分頑健である必要がある

という3つの問題があるからです。
Brentの方法（Brent's method; Brent, 1973）は、あらゆる場合において、上記の3つの問題を解決する優れた方法です。なお、非線形方程式の求根アルゴリズムにも、同名の方法が存在しますが、これとはまた別です。Brentの方法の詳しい説明は割愛しますが、興味のある方は参考文献[1]等を参照して下さい。

補足（導関数が解析的に求められる場合）

対象の関数$f\left( x\right)$の導関数$f^{\prime}\left( x\right) $が解析的に求められる場合、Brentの方法よりも効率の良いアルゴリズムが存在します。このアルゴリズムの詳細については、参考文献[1]を参照して下さい。

Boost C++ Librariesによる実装と利用

C++では、Brentの方法はBoost C++ Librariesにbrent_find_minima関数として実装されています。
brent_find_minima関数を利用するには、boost/math/tools/minima.hppのインクルードが必要で、そこでは以下のように定義されています。

template <class F, class T>
std::pair<T, T> brent_find_minima(F f, T min, T max, int bits);

template <class F, class T>
std::pair<T, T> brent_find_minima(F f, T min, T max, int bits, boost::uintmax_t& max_iter);

一つ目のオーバーロードでは、引数は、

f: 最小値探索対象の関数オブジェクト
min: 最小値探索範囲の下限（区間[a,b]のa）
max: 最小値探索範囲の上限（区間[a,b]のb）
bits: 最小値探索の精度をビットで指定（環境によると思いますが、x86_64環境で、倍精度浮動小数点型を使用した場合には、20ビットが上限のようです）

を取ります。二つ目のオーバーロードでは、それに加えて、

max_iter: 最小値探索の最大繰り返し回数

を取ります。
brent_find_minima関数の戻り値は、

Returns: 関数が最小値を取るときのxの値と、最小値の組のstd::pair

です。
実際にこの関数を使用する際には、max_iterを指定して、二つ目のオーバーロードを使用した方が無難でしょう。

具体例

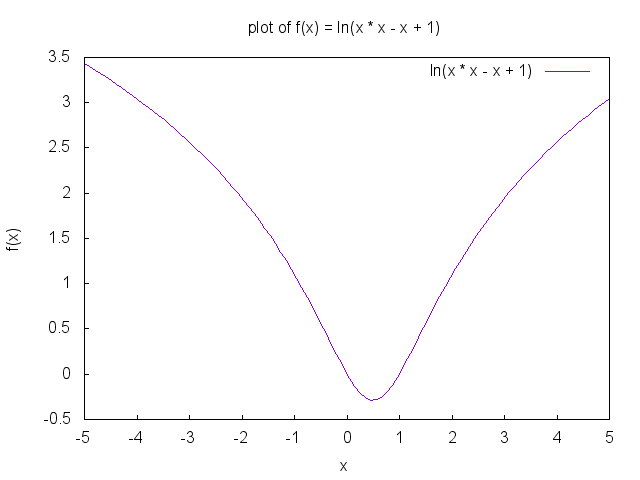
1次元の関数$f\left( x\right) =\ln\left( x^{2}-x+1\right) $の最小値を求めてみましょう。最小値は、$f\left( \dfrac{1}{2}\right) =\ln\left( \dfrac{3}{4}\right) \simeq
-0.287682072451781$と、簡単に解析的に求まります。なお、$f\left( x\right)$のプロットは以下のようになります。

それでは、この関数の最小値を、Brentの方法によって数値的に求めてみましょう。以下にサンプルコードを示します。

#include <iostream>                     // for std::cout, std::endl
#include <boost/format.hpp>             // for boost::format
#include <boost/math/tools/minima.hpp>  // for boost::math::tools::brent_find_minima

int main()
{
    // 最大繰り返し回数100回
    boost::uintmax_t max_iter = 100;

    // f(x) = ln(x * x - x + 1)なる関数の最小値を、区間[-5.0, 5.0]において、
    // 精度20ビットで探索する。
    // ただし、探索回数が最大繰り返し回数に達したときは探索を打ち切る
    auto const r = boost::math::tools::brent_find_minima(
        [](double x) { return std::log(x * x - x + 1); },
        -5.0,
        5.0,
        20,
        max_iter);

    // 結果を表示
    std::cout << boost::format("x = %.15f f = %.15f") % r.first % r.second << std::endl;

    return 0;
}

// output
// x = 0.499999811477940 f = -0.287682072451734

このサンプルコードの例では、$f\left( x\right)$が最小値を取るときのxの値は小数点以下第6位まで、$f\left( x\right)$の最小値の値は小数点以下第13位まで正しく求められていることが分かります。

まとめ

1次元の関数を数値的に最小化する方法として、黄金分割法とBrentの方法を紹介しました。
Brentの方法の実装として、Boost C++ Librariesのbrent_find_minima関数を紹介しました。
実際にbrent_find_minima関数を用いて、1次元の関数の最小化を行いました。

参考文献

[1] William H. Press, William T. Vetterling, Saul A. Teukolsky, Brian P. Flannery 『ニューメリカルレシピ・イン・シー日本語版―C言語による数値計算のレシピ』技術評論社（1993）
[2] 黄金分割探索 - Wikipedia

Boost C++ Librariesのbrent_find_minima（Brentの方法）による1次元関数の最小化