マビノギというオンラインRPGに、以下の画像のようなミニゲームがあります。
要するに、左のルーレットを回して当たった数字で、右のビンゴボードを埋めていくというミニゲームです(以下の画像のような感じ)。
このビンゴゲームについて、ビンゴのマスを全て埋めるために必要な、ルーレットの試行回数の期待値を考えます。これは、いわゆるクーポンコレクター問題であり、25種類のクーポンを全て揃えるために必要な試行回数の期待値E(N)と同じですから、
E(N)=25%
%TCIMACRO{\dsum \limits_{n=1}^{25}}%
%BeginExpansion
{\displaystyle\sum\limits_{n=1}^{25}}
%EndExpansion
\dfrac{1}{n}\simeq95.4
です。
本題
しかしながら、一つの行・列が揃うために必要なルーレットの試行回数の期待値を求めたかったため、C++11C++14(知らず知らずのうちにC++14を使っていたので、せっかくなので全てC++14で書き直しました。と言っても数ヶ所修正しただけですが。)でモンテカルロ・シミュレーションを行いました。
以下にコードをそのまま載せます。
# include "myrand.h"
# include <algorithm> // for std::find, std::shuffle, std::sort, std::transform
# include <cstdint> // for std::int32_t
# include <cmath> // for std::sqrt
# ifdef OUTPUTCSV
#include <fstream> // for std::ofstream
# endif
# include <iostream> // for std::cout
# include <iomanip> // for std::setiosflags, std::setprecision
# include <iterator> // for std::begin
# include <map> // for std::map
# include <numeric> // for std::iota
# include <random> // for std::mt19937
# include <tuple> // for std::tie
# include <unordered_map> // for std::unordered_map
# include <utility> // for std::make_pair
# include <vector> // for std::vector
# include <valarray> // for std::valarray
namespace {
//! A global variable (constant expression).
/*!
列のサイズ
*/
static auto constexpr COLUMN = 5U;
//! A global variable (constant expression).
/*!
行のサイズ
*/
static auto constexpr ROW = 5U;
//! A global variable (constant expression).
/*!
ビンゴボードのマス数
*/
static auto constexpr BOARDSIZE = ROW * COLUMN;
//! A global variable (constant expression).
/*!
モンテカルロシミュレーションの試行回数
*/
static auto constexpr MCMAX = 10000U;
//! A global variable (constant expression).
/*!
行・列の総数
*/
static auto constexpr ROWCOLUMN = ROW + COLUMN;
//! A typedef.
/*!
そのマスに書かれてある番号と、そのマスが当たったかどうかを示すフラグのstd::pair
*/
using mypair = std::pair<std::int32_t, bool>;
//! A typedef.
/*!
行・列が埋まるまでに要した回数と、その時点で埋まったマスのstd::pair
*/
using mypair2 = std::pair<std::int32_t, std::int32_t>;
//! A typedef.
/*!
(n + 1)個目の行・列が埋まったときの分布を格納するためのmapの型
*/
using mymap = std::map<std::int32_t, std::int32_t>;
//! A function.
/*!
(n + 1)個目の行・列が埋まったときの平均試行回数、埋まっているマスの平均個数を求める
\param mcresult モンテカルロ・シミュレーションの結果が格納された二次元可変長配列
\return (n + 1)個目の行・列が埋まったときの平均試行回数、埋まっているマスの平均個数が格納された可変長配列のstd::pair
*/
std::pair< std::valarray<double>, std::valarray<double> > eval_average(std::vector< std::vector<mypair2> > const & mcresult);
//! A function.
/*!
(n + 1)個目の行・列が埋まったときの中央値を求める
\param (n + 1)個目の数値n
\param mcresult モンテカルロ・シミュレーションの結果が格納された二次元可変長配列
\return (n + 1)個目の行・列が埋まったときの中央値
*/
std::int32_t eval_median(std::vector< std::vector<mypair2> > const & mcresult, std::int32_t n);
//! A function.
/*!
(n + 1)個目の行・列が埋まったときの最頻値と分布を求める
\param (n + 1)個目の数値n
\param mcresult モンテカルロ・シミュレーションの結果が格納された二次元可変長配列
\return (n + 1)個目の行・列が埋まったときの最頻値と分布のstd::pair
*/
std::pair<std::int32_t, std::map<std::int32_t, std::int32_t> > eval_mode(std::vector< std::vector<mypair2> > const & mcresult, std::int32_t n);
//! A function.
/*!
(n + 1)個目の行・列が埋まったときの標準偏差を求める
\param avgten (n + 1)個目の行・列が埋まったときの平均試行回数
\param (n + 1)個目の数値n
\param mcresult モンテカルロ・シミュレーションの結果が格納された二次元可変長配列
\return (n + 1)個目の行・列が埋まったときの標準偏差
*/
double eval_std_deviation(double avg, std::vector< std::vector<mypair2> > const & mcresult, std::int32_t n);
//! A function.
/*!
ビンゴボードを生成する
\return ビンゴボードが格納された可変長配列
*/
auto makeboard();
//! A function.
/*!
モンテカルロ・シミュレーションを行う
\return モンテカルロ・シミュレーションの結果が格納された二次元可変長配列
*/
std::vector< std::vector<mypair2> > montecarlo();
//! A function.
/*!
モンテカルロ・シミュレーションの実装
\param mr 自作乱数クラスのオブジェクト
\return モンテカルロ法の結果が格納された可変長配列
*/
std::vector<mypair2> montecarloImpl(myrandom::MyRand & mr);
# ifdef OUTPUTCSV
//! A function.
/*!
(n + 1)個目の行・列が埋まったときの分布をcsvファイルに出力する
\param distmap (n + 1)個目の行・列が埋まったときの分布
\param (n + 1)個目の数値n
*/
void outputcsv(mymap const & distmap, std::int32_t n);
# endif
}
int main()
{
// モンテカルロ・シミュレーションの結果を代入
auto const mcresult(montecarlo());
std::valarray<double> trialavg, fillavg;
std::tie(trialavg, fillavg) = eval_average(mcresult);
std::cout << std::setprecision(1) << std::setiosflags(std::ios::fixed);
for (auto n = 0U; n < ROWCOLUMN; n++) {
std::int32_t mode;
std::map<std::int32_t, std::int32_t> distmap;
std::tie(mode, distmap) = eval_mode(mcresult, n);
# ifdef OUTPUTCSV
outputcsv(distmap, n);
# endif
std::cout
<< (n + 1)
<< "個目に必要な平均試行回数:"
<< trialavg[n]
<< "回, 効率:"
<< (trialavg[n] / static_cast<double>(n + 1))
<< "(回/個), "
<< "中央値:"
<< eval_median(mcresult, n)
<< "回, 最頻値:"
<< mode
<< "回, 標準偏差:"
<< eval_std_deviation(trialavg[n], mcresult, n)
<< ", 埋まっているマスの平均個数:"
<< fillavg[n]
<< "個\n";
}
return 0;
}
namespace {
std::pair< std::valarray<double>, std::valarray<double> > eval_average(std::vector< std::vector<mypair2> > const & mcresult)
{
// モンテカルロ・シミュレーションの平均試行回数の結果を格納した可変長配列
std::valarray<double> trialavg(ROWCOLUMN);
// モンテカルロ・シミュレーションのn回目の試行で、埋まっているマスの数を格納した可変長配列
std::valarray<double> fillavg(ROWCOLUMN);
// 行・列の総数分繰り返す
for (auto n = 0U; n < ROWCOLUMN; n++) {
// 総和を0で初期化
auto trialsum = 0;
auto fillsum = 0;
// 試行回数分繰り返す
for (auto j = 0U; j < MCMAX; j++) {
// j回目の結果を加える
trialsum += mcresult[j][n].first;
fillsum += mcresult[j][n].second;
}
// 平均を算出してn行・列目のtrialavg、fillavgに代入
trialavg[n] = static_cast<double>(trialsum) / static_cast<double>(MCMAX);
fillavg[n] = static_cast<double>(fillsum) / static_cast<double>(MCMAX);
}
return std::make_pair(std::move(trialavg), std::move(fillavg));
}
std::int32_t eval_median(std::vector< std::vector<mypair2> > const & mcresult, std::int32_t n)
{
// 中央値を求めるために必要な可変長配列
std::vector<std::int32_t> medtmp(MCMAX);
// 中央値を求めるために必要な可変長配列を、モンテカルロ法の結果から生成
std::transform(
mcresult.begin(),
mcresult.end(),
medtmp.begin(),
[n](auto const & res) { return res[n].first; });
// 中央値を求めるためにソートする
std::sort(medtmp.begin(), medtmp.end());
// 中央値を求める
if (MCMAX % 2) {
// 要素が奇数個なら中央の要素を返す
return medtmp[(MCMAX - 1) / 2];
}
else {
// 要素が偶数個なら中央二つの平均を返す
return (medtmp[(MCMAX / 2) - 1] + medtmp[MCMAX / 2]) / 2;
}
}
std::pair<std::int32_t, mymap> eval_mode(std::vector< std::vector<mypair2> > const & mcresult, std::int32_t n)
{
// (n + 1)個目の行・列が埋まったときの分布
std::unordered_map<std::int32_t, std::int32_t> distmap;
// distmapを埋める
for (auto const & res : mcresult) {
// (n + 1)個目の行・列が埋まったときの回数をkeyとする
auto const key = res[n].first;
// keyが存在するかどうか
auto itr = distmap.find(key);
if (itr == distmap.end()) {
// keyが存在しなかったので、そのキーでハッシュを拡張(値1)
distmap.emplace(key, 1);
}
else {
// keyが指す値を更新
itr->second++;
}
}
// 最頻値を探索
auto const mode = std::max_element(
distmap.begin(),
distmap.end(),
[](auto const & p1, auto const & p2) { return p1.second < p2.second; })->first;
// 最頻値と(n + 1)個目の行・列が埋まったときの分布をpairにして返す
return std::make_pair(mode, mymap(distmap.begin(), distmap.end()));
}
double eval_std_deviation(double avg, std::vector< std::vector<mypair2> > const & mcresult, std::int32_t n)
{
// 標準偏差を求めるために必要な可変長配列
std::valarray<double> devtmp(MCMAX);
// 標準偏差の計算
std::transform(
mcresult.begin(),
mcresult.end(),
std::begin(devtmp),
[avg, n](auto const & res) {
auto const val = static_cast<double>(res[n].first);
return (val - avg) * (val - avg);
});
// 標準偏差を求める
return std::sqrt(devtmp.sum() / static_cast<double>(MCMAX));
}
auto makeboard()
{
// 仮のビンゴボードを生成
std::vector<std::int32_t> boardtmp(BOARDSIZE);
// 仮のビンゴボードに1~25の数字を代入
std::iota(boardtmp.begin(), boardtmp.end(), 1);
// 仮のビンゴボードの数字をシャッフル
std::shuffle(boardtmp.begin(), boardtmp.end(), std::mt19937());
// ビンゴボードを生成
std::vector<mypair> board(BOARDSIZE);
// 仮のビンゴボードからビンゴボードを生成する
std::transform(
boardtmp.begin(),
boardtmp.end(),
board.begin(),
[](auto n) { return std::make_pair(n, false); });
// ビンゴボードを返す
return board;
}
std::vector< std::vector<mypair2> > montecarlo()
{
// モンテカルロ・シミュレーションの結果を格納するための二次元可変長配列
std::vector< std::vector<mypair2> > mcresult;
// MCMAX個の容量を確保
mcresult.reserve(MCMAX);
// 自作乱数クラスを初期化
myrandom::MyRand mr(1, BOARDSIZE);
// 試行回数分繰り返す
for (auto i = 0U; i < MCMAX; i++) {
// モンテカルロ・シミュレーションの結果を代入
mcresult.push_back(montecarloImpl(mr));
}
// モンテカルロ・シミュレーションの結果を返す
return mcresult;
}
std::vector<mypair2> montecarloImpl(myrandom::MyRand & mr)
{
// ビンゴボードを生成
auto board(makeboard());
// その行・列が既に埋まっているかどうかを格納する可変長配列
// ROWCOLUMN個の要素をfalseで初期化
std::vector<bool> rcfill(ROWCOLUMN, false);
// 行・列が埋まるまでに要した回数と、その時点で埋まったマスを格納した
// 可変長配列
std::vector<mypair2> fillnum;
// ROWCOLUMN個の容量を確保
fillnum.reserve(ROWCOLUMN);
// その時点で埋まっているマスを計算するためのラムダ式
auto const sum = [](auto const & vec) {
auto cnt = 0;
for (auto & e : vec) {
if (e.second) {
cnt++;
}
}
return cnt;
};
// 無限ループ
for (auto i = 1; ; i++) {
// 乱数で得た数字で、かつまだ当たってないマスを検索
auto itr = std::find(board.begin(), board.end(), std::make_pair(mr.myrand(), false));
// そのようなマスがあった
if (itr != board.end()) {
// そのマスは当たったとし、フラグをtrueにする
itr->second = true;
}
// そのようなマスがなかった
else {
//ループ続行
continue;
}
// 各行・列が埋まったかどうかをチェック
for (auto j = 0U; j < ROW; j++) {
// 各行が埋まったかどうかのフラグ
auto rowflag = true;
// 各行が埋まったかどうかをチェック
for (auto k = 0U; k < COLUMN; k++) {
rowflag &= board[COLUMN * j + k].second;
}
// 行の処理
if (rowflag &&
// その行は既に埋まっているかどうか
!rcfill[j]) {
// その行は埋まったとして、フラグをtrueにする
rcfill[j] = true;
// 要した試行回数と、その時点で埋まったマスの数を格納
fillnum.push_back(std::make_pair(i, sum(board)));
}
// 各列が埋まったかどうかのフラグ
auto columnflag = true;
// 各列が埋まったかどうかをチェック
for (auto k = 0U; k < ROW; k++) {
columnflag &= board[j + COLUMN * k].second;
}
// 列の処理
if (columnflag &&
// その列は既に埋まっているかどうか
!rcfill[j + ROW]) {
// その列は埋まったとして、フラグをtrueにする
rcfill[j + ROW] = true;
// 要した試行回数と、その時点で埋まったマスの数を格納
fillnum.push_back(std::make_pair(i, sum(board)));
}
}
// 全ての行・列が埋まったかどうか
if (fillnum.size() == ROWCOLUMN) {
// 埋まったのでループ脱出
break;
}
}
// 要した試行関数の可変長配列を返す
return fillnum;
}
# ifdef OUTPUTCSV
void outputcsv(mymap const & distmap, std::int32_t n)
{
std::ofstream ofs((boost::format("distribution_%d個目.csv") % (n + 1)).str());
boost::transform(
distmap,
std::ostream_iterator<std::string>(ofs, "\n"),
[](auto const & p) { return (boost::format("%d,%d") % p.first % p.second).str(); });
}
# endif
}
myrand.hの内容は載せていませんが、paiza.IOに全てのコード(と実行結果)が載せてあります( https://paiza.io/projects/WznXiKop9v97Xp7AA8Gs7A )。
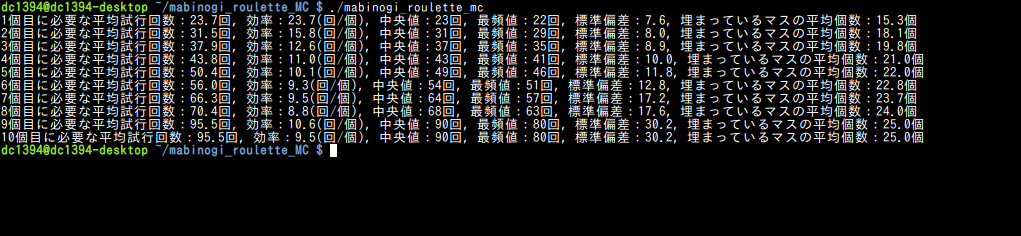
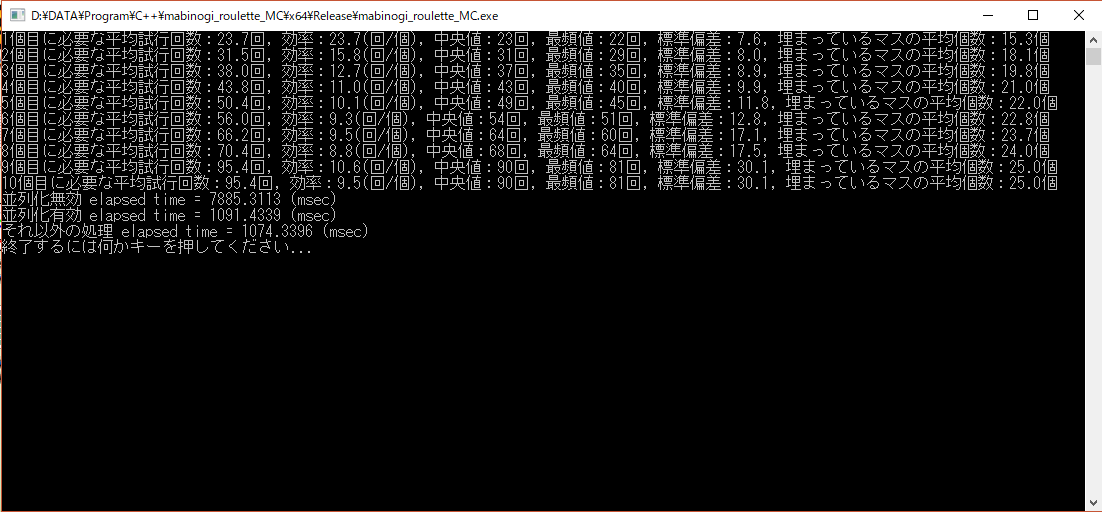
実行結果は以下のようになります。
10個目に必要な平均試行回数が95.5回と計算されていることから、理論値とほぼ等しく、バグってはいないことが分かります(試行回数10000回)。
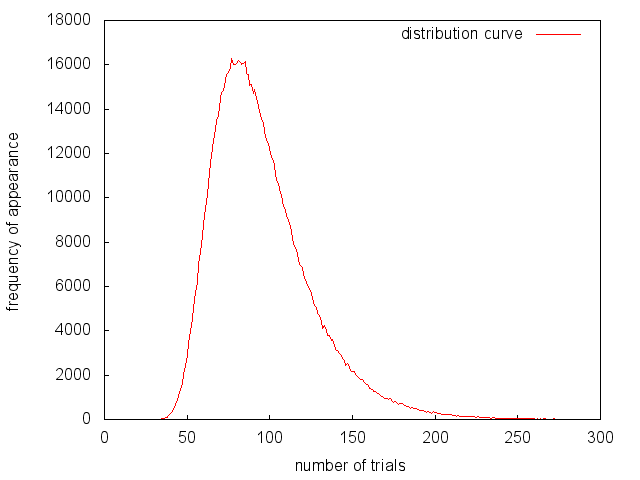
また、標準偏差の値が約30で、しかも最頻値、中央値、平均値の順に大きくなっており、さらにそれらの値の差が大きいことから、典型的な(右に)裾の重い(長い)分布であることが分かります。なお、分布の様子を図にプロットすると、以下のようになります(ただし、試行回数100万回の場合)。
並列化
Intel Threading Building Blocks (Intel TBB)による並列化
一般にモンテカルロ法は、並列化効率が非常に高いことで知られています。せっかくなので、Intel Threading Building Blocks (Intel TBB)(以下単にTBBと呼ぶ)で並列化してみることにしました(ついでに、Boostも使っています)。並列化と言っても、何も難しいことはありません。関数montecarlo()を、以下のように書き換えるだけです。
tbb::concurrent_vector< std::vector<mypair2> > montecarloTBB()
{
// モンテカルロ・シミュレーションの結果を格納するための二次元可変長配列
// 複数のスレッドが同時にアクセスする可能性があるためtbb::concurrent_vectorを使う
tbb::concurrent_vector< std::vector<mypair2> > mcresult;
// MCMAX個の容量を確保
mcresult.reserve(MCMAX);
// MCMAX回のループを並列化して実行
tbb::parallel_for(
0U,
MCMAX,
1U,
[&mcresult](auto) {
// 自作乱数クラスを初期化
myrandom::MyRand mr(1, BOARDSIZE);
// モンテカルロ・シミュレーションの結果を代入
mcresult.push_back(montecarloImpl(mr));
});
}
単に、forループをtbb::paralle_for(tbb/paralle_for.hで定義されています)に書き換えているだけです。注意点としては、変数mcresultは、複数のスレッドから同時にアクセスされるため、std::vector<T>ではなく、tbb::concurrent_vector<T>(tbb/concurrent_vector.hで定義されています)を使わなければならない点と、乱数生成クラスのオブジェクトを、スレッド別に持たなければならないため、tbb::paralle_forループ内部で乱数生成クラスのオブジェクトを生成している点です。
並列化してみたコードは、GitHubのここ(なお、Boost C++ Librariesも使用しています)にアップロードしています。
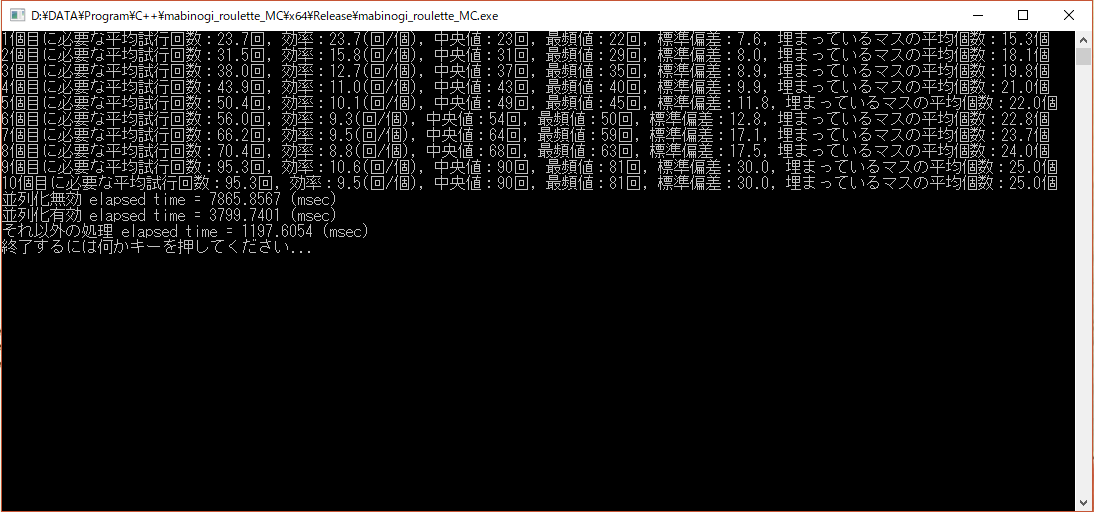
試行回数を100万回にして、並列化の速度向上を、以下の環境
- CPU: Intel Core i7-7820X (Skylake-X, Hyper Threading ON (8C16T), SpeedStep OFF, Turbo Boost OFF)
- 物理メモリ:32GB
- OS:Windows 10 Enterprise x64
- コンパイラ:Visual C++ 2015 (VC14) x64ビルド
で測定しますと、以下の画像のようになりました。
以上のように、並列化効率は約2.0倍になっています。
Intel Cilk Plusによる並列化
並列化の速度向上に満足できなかったため、TBBの代わりに、Intel Cilk Plus(以下単にCilkと呼ぶ)で並列化してみることにしました。Cilkによる並列化は、TBBによる並列化よりもさらに簡単で、以下のコードのように、関数montecarlo()のforループを単にcilk_forに書き換えるだけで済みます。
tbb::concurrent_vector< std::vector<mypair2> > montecarloCilk()
{
// モンテカルロ・シミュレーションの結果を格納するための二次元可変長配列
// 複数のスレッドが同時にアクセスする可能性があるためtbb::concurrent_vectorを使う
tbb::concurrent_vector< std::vector<mypair2> > mcresult;
// MCMAX個の容量を確保
mcresult.reserve(MCMAX);
// MCMAX回のループを並列化して実行
cilk_for (auto i = 0U; i < MCMAX; i++) {
// 自作乱数クラスを初期化
myrandom::MyRand mr(1, BOARDSIZE);
// モンテカルロ・シミュレーションの結果を代入
mcresult.push_back(montecarloImpl(mr));
});
// モンテカルロ・シミュレーションの結果を返す
return mcresult;
}
TBBによる並列化の際と同様に、変数mcresultは、複数のスレッドから同時にアクセスされるため、std::vector<T>ではなく、tbb::concurrent_vector<T>(tbb/concurrent_vector.hで定義されています)を使わなければなりません。また、乱数生成クラスのオブジェクトを、スレッド別に持たなければならないため、cilk_forループ内部で乱数生成クラスのオブジェクトを生成しなければならない点も、TBBによる並列化の場合と同様です。
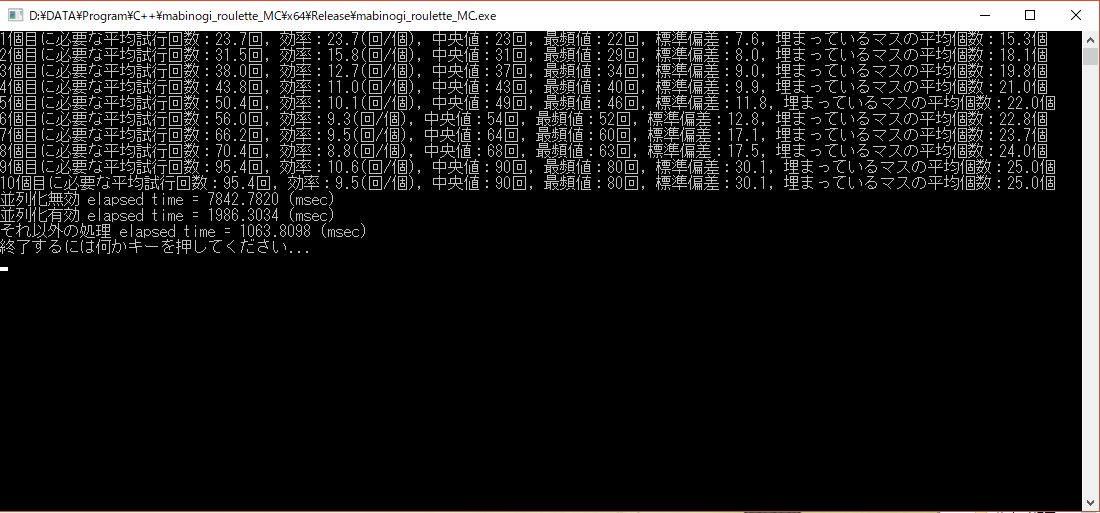
試行回数を100万回にして、並列化の速度向上を、以下の環境
- CPU: Intel Core i7-7820X (Skylake-X, Hyper Threading ON (8C16T), SpeedStep OFF, Turbo Boost OFF)
- 物理メモリ:32GB
- OS:Windows 10 Enterprise x64
- コンパイラ:Intel C++ Compiler 17.0.4 x64ビルド
で測定しますと、以下の画像のようになりました。
以上のように、並列化効率は約3.9倍になっています。
余談
ちなみに、乱数生成エンジンとして、C++11標準のメルセンヌ・ツイスター乱数生成エンジンの代わりに、Intel C++ Compilerに付属している、AVX-512命令を使用したメルセンヌ・ツイスター乱数生成エンジンを使いますと、並列化の速度向上は以下の画像のようになりました(実行環境は、Intel Cilk Plusで並列化したときと同じです)。
以上のように、並列化効率は約7.2倍になっています。
まとめ
TBBよりCilkの方が賢いらしい。AVX-512はさすがに速い。