自己紹介

こんにちは。某大学の某情報学部で量子計算・量子ネットワークの研究室に所属しているdaveと申します。コンピュータサイエンスの観点から量子情報技術を研究している、世界的に見ても稀有な研究室です。自分の主な興味は大規模量子計算アーキテクチャ（特に分散量子計算)で、卒論では自作分散量子計算シミュレーターを使って、今後必要になると考えられる機能の提案・検証しています。

コンピュータサイエンスの観点から量子情報技術を研究する意義

量子情報技術の世界的な勢力図の最大派閥は物理屋さんです。主に量子計算の理論とハードウェア開発で大活躍をされています。しかし量子コンピュータや量子ネットワークを情報システムとして動かす時に、歴史の長い古典のコンピュータアーキテクチャ、ネットワークアーキテクチャの概念を応用することで量子コンピュータや量子ネットワークの機能を拡張することができます。

この記事の目的

読者の皆様に分散量子計算の意義と、分散量子計算システムにはどのようなものが必要かを知って頂ければと思っております。量子コンピュータアドベントカレンダーの参加者の皆さんは例年物理屋さんが大半を占めており、物理を知らないのに量子コンピュータの勉強をしていたことに引け目を感じていたのですが、分散量子計算に本格的に取り組んでから「計算機屋がいないとこのシステムは実世界で動かせない」という確信を得たので、計算機屋らしくシステムの話をします笑

なぜ分散量子計算を行うのか

大規模量子計算の実現には大きく分けて2つのアプローチが提案されています。1つは単独の大規模量子プロセッサを構築するアプローチ、そしてもう1つが小-中規模の量子プロセッサを複数使って分散コンピューティング的に量子計算を行うアプローチです。

このカレンダーをご覧になっている方は、IBMやGoogleが事あるごとに量子プロセッサの規模を拡大しているのをご存知だと思うので前者の方針には馴染みがあると思いますが、後者のアプローチを取ると以下のようなアドバンテージがあります。

各プロセッサに要求される技術的なハードルが低い
- 量子コンピュータの演算はハードウェア上のノイズの影響で、実行している演算の規模が大きくなればなるほど量子状態が正確さを失います。逆にいうと、中規模の量子プロセッサで行うそれなりの規模の演算(e.g. 256桁の合成数の素因数分解のための周期発見)と大規模の量子プロセッサをフルに使って行う演算(2048桁の合成数の素因数分解のための周期発見)で同じフィデリティ¹を実現しようと思ったら、大規模なプロセッサの方により低いエラー率が要求されることが分かります。エラー率の低減と大規模化はどの物理系においても重大な課題なので、それであれば中規模な量子プロセッサを複数集めて結果的に大規模な量子計算ができるようにした方が現実的だというのがご理解頂けるかと思います。
耐故障性がある
- 分散システムの利点の1つに「システムの一部(e.g.サーバーやプロセッサ)が故障しても他のシステムを使ってカバーできる」というものがあります。逆に単独の大規模量子プロセッサが何かの調子で故障してしまったら利用者全員に迷惑がかかります。(こういう存在を単一障害点、single point failureと言います)

分散量子計算システムの各コンポーネント

今回は分散量子計算のレビュー論文の内容に自分なりの考えをプラスして分散量子計算システムに必要であろうレイヤーについて記述していきます。

量子アルゴリズム

　まずはもちろん、量子コンピュータで行う計算です。学術的または商業的に価値のある問題で、かつ量子計算の方が何かしらのアドバンテージ(e.g. 計算量の減少)があるアルゴリズムこそ、量子コンピュータの存在意義であり、人々が量子コンピュータを研究する理由です。　もう既に分散量子計算バージョンのショアのアルゴリズムとグローバーのアルゴリズムは提案されてはいますが、個人的にはそのような分散化は次の分散量子コンパイラの役割だと考えています。

分散量子コンパイラ

　ご存知のない方のために説明すると、コンパイラは人間が書いたプログラミング言語を機械が実行可能な形式に変換して、また実行にかかる時間やリソースを最適化するソフトウェアのことを指します。Qiskitをはじめとする量子計算フレームワークは量子コンパイラを持っており、実機の物理量子ビットの接続性を考慮した使用量子ビットの選定、ユーザープログラムからプロセッサ上で実行可能なゲートセットへの翻訳、エラーの影響軽減のための量子回路最適化を全部担っています。

このような分散量子コンパイラ特有の機能の1つに、non-local CNOT(別の量子プロセッサ上の量子ビット間にかけるCNOTゲート)をクラスタ上で実行できるゲートに分解するというものがあります。
non-local CNOTには

双方向の1古典ビットのやりとりで実現する方法(tele-gate strategy, entanglement swapping strategy)
CNOTのコントロール量子ビットをターゲット量子ビットの同じプロセッサまで量子テレポーテーションで移動させて、CNOTをかけた後に元の量子プロセッサまで戻す方法(tele-data strategy)
SWAPゲートを使ってコントロール量子ビットとターゲット量子ビットが隣り合うようにする方法(data-qubit swapping based strategy)があります。

昨年publishされた分散量子コンパイラの論文では1番目と3番目の性能比較が議論されていました。また、今年出た論文では2番目の方法で必要な量子テレポーテーションの回数を減らすための最適化手法が提案されていました。

量子プロセッサクラスタ (仮想量子プロセッサ)

上のレビュー論文では殆ど機能について議論されていませんが、個人的にはこのレイヤーこそが古典の分散システムの知見が活かせる場所だと考えています。分散量子計算の実装レベルの論文では集中型コンピューティング (あるサーバーがクラスタ全体の情報を元に各プロセッサにプロセスを割り当てる方式)が暗黙の前提とされていますが、分散型コンピューティング (各プロセッサが協働して与えられたタスクを終わらせる方式）の方がよりロバストで耐障害性が高いと考えています。
分散型分散量子計算に必要なリーダー選挙や排他制御はどのように実装するのか、障害検知や障害回復はどのように行うのか、この方式に適した「分散型分散量子コンパイラ」はどのようなものなのか等、重要な問題が数多く残されている宝の山です。

量子プロセッサ

量子プロセッサ自体は既に存在しているのですが、同じ種類のプロセッサ間の分散量子計算だけでなく、違う物理アーキテクチャのプロセッサ同士で行う分散量子計算(ヘテロジニアス量子計算)の実行方法も今後議論されると予想しています。

量子ネットワーク

量子ネットワークとは量子情報を伝送するネットワーク技術で、通常古典ネットワークと併用して使用されます。以下が具体的な方法です。(画像は研究室の先輩の解説記事から引用しました)
まず、量子コンピュータの間に複数の量子中継器(量子通信を中継するノード)を設置して各リンクごとにBell pairを構築します。

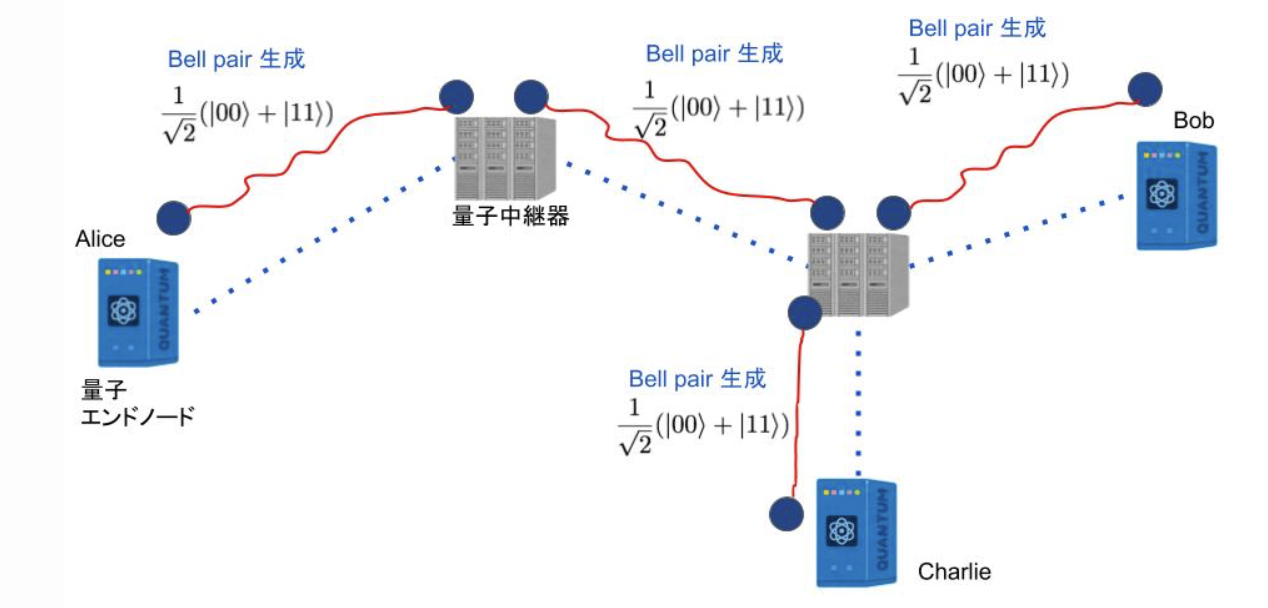
次に、量子中継器上の量子ビットを測定して、測定結果を中継器と隣り合うノードに古典ネットワーク経由で送信します。（この操作をEntanglement swappingと言います)

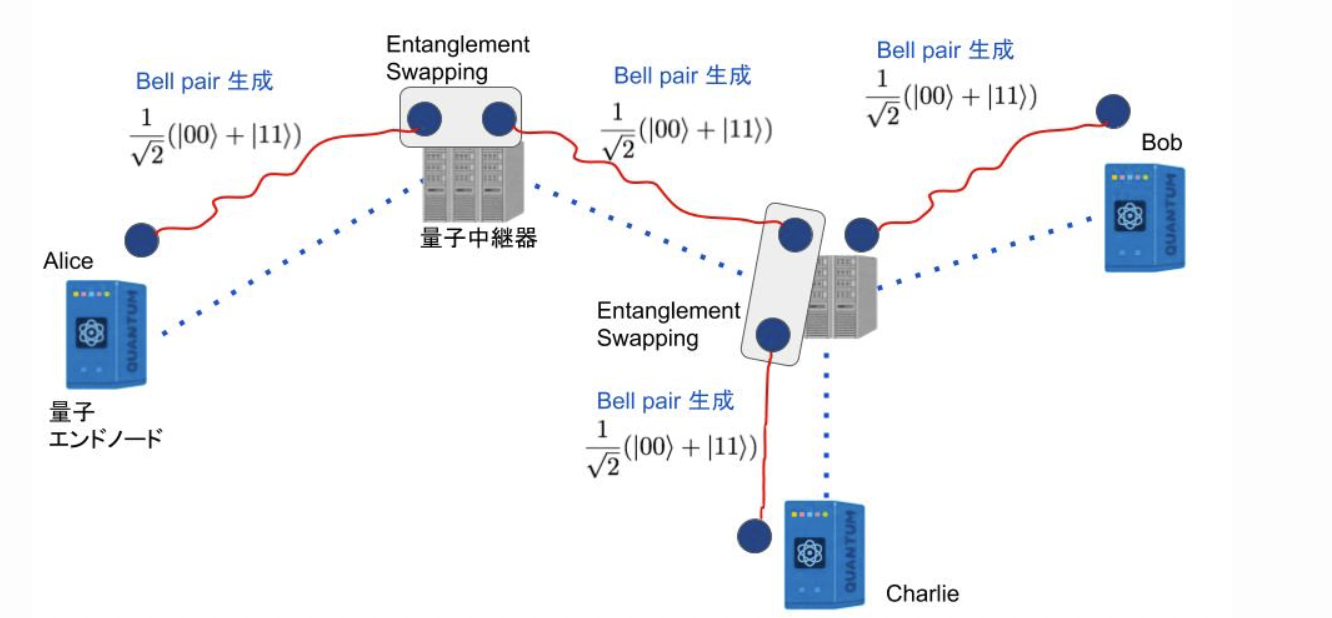
この操作を繰り返すとEnd-to-EndのBell pairが出来ます。

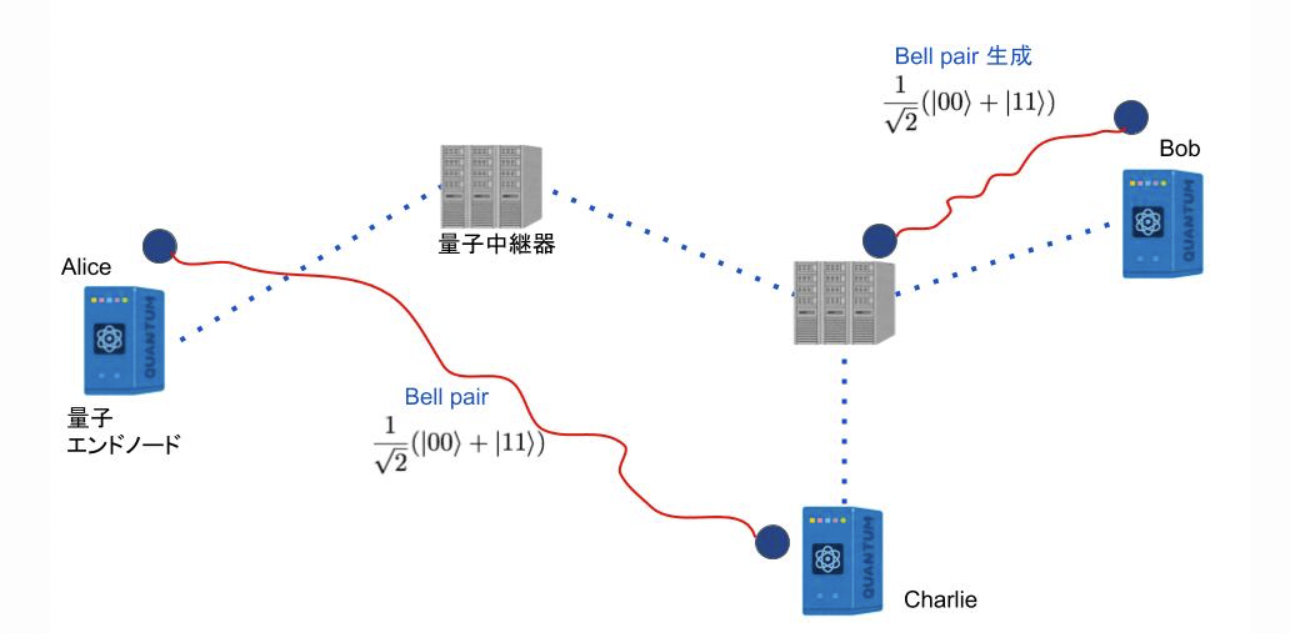
このEnd-to-EndのBell pairは、隣り合ってない量子プロセッサ上の量子ビット間でCNOTゲートを実行時の消費リソースなどに使えます。

最後に

この記事では分散量子計算に必要なコンポーネントを解説してきました。少しでも分散量子計算の理解が深まるきっかけになれば幸いです。先述の自作分散量子計算シミュレータですが、卒論を論文化しようという話になっているので、論文がarXivに上がった段階で公開します。
また改めてシミュレータの解説記事も書こうと思っているのでそちらもご覧下さい。

参考文献

[1]Vasil S. Denchev and Gopal Pandurangan. 2008. Distributed quantum computing: a new frontier in distributed systems or science fiction? SIGACT News 39, 3 (September 2008), 77–95. DOI:https://doi.org/10.1145/1412700.1412718
[2]Cuomo, Daniele, Marcello Caleffi, and Angela Sara Cacciapuoti. "Towards a distributed quantum computing ecosystem." IET Quantum Communication 1.1 (2020): 3-8.
[3]Yimsiriwattana, Anocha, and Samuel J. Lomonaco Jr. "Distributed quantum computing: A distributed Shor algorithm." Quantum Information and Computation II. Vol. 5436. International Society for Optics and Photonics, 2004.
[4]Exman, Iaakov & Levy, Efrat. (2012). Quantum Probes Reduce Measurements: Application to Distributed Grover Algorithm. arXiv:1208.3905.
[5]Eisert, Jens, et al. "Optimal local implementation of nonlocal quantum gates." Physical Review A 62.5 (2000): 052317.
[6]Meter, Rodney Van, et al. "Arithmetic on a distributed-memory quantum multicomputer." ACM Journal on Emerging Technologies in Computing Systems (JETC) 3.4 (2008): 1-23.
[7]Ferrari, Davide, et al. "Compiler Design for Distributed Quantum Computing." arXiv preprint arXiv:2012.09680 (2020).
[8]Ghodsollahee, I., Davarzani, Z., Zomorodi, M. et al. Connectivity matrix model of quantum circuits and its application to distributed quantum circuit optimization. Quantum Inf Process 20, 235 (2021). https://doi.org/10.1007/s11128-021-03170-5
[9]S. Krishnaprasad. 2004. A gentle introduction to distributed algorithms. In Proceedings of the 2nd annual conference on Mid-south college computing (MSCCC '04). Mid-South College Computing Conference, Little Rock, Arkansas, USA, 28–35.
[10]Tani, Seiichiro, Hirotada Kobayashi, and Keiji Matsumoto. "Exact quantum algorithms for the leader election problem." Annual Symposium on Theoretical Aspects of Computer Science. Springer, Berlin, Heidelberg, 2005.
[11]猫でもわかる量子インターネット - Shota Nagayama's Quantum Internet Research Lab. https://shota.io/2019/12/24/quantum-internet.html (閲覧日時2021年12月12日)

0~1で表される2つの量子状態の近さの尺度　特に現実の量子状態がどれぐらい理論的な純粋状態に近いかを表すときに使われることが多い。 ↩

分散量子計算入門