マッチングアプリ強者の統計をとってみた＆機械学習モデルを作成してみた

#序章
みなさんこんにちは。

マッチングアプリ使ってますか？！
私は最近マッチングアプリでマッチした方の一人といい感じです。

ところで、私の使っていたマッチングアプリは他の人気会員のデータが参照できました。
（おそらく１００ライク以上もらっている人が表示されます。）

それを見た私は悔しくてたまりませんでした。

「ライク、１００ももらってないんだけど...」
「俺も１００を超える男になりたい」

そう強く思いました。

同時に、どうすれば「１００を超える男」になれるのか？
そういう思いでデータを解析してみました。

#データ収集
＊機械学習のための著作権法改定により問題ないと解釈しております。
＊データサイエンスはくそ初心者です。間違いがある可能性があります。

地道に他の会員データを手入力（Google Documentの文字起こしをフル活用）し、約60件のデータを集めました。

表示される他会員のデータは、私の年齢である３２歳に近い年齢の人が表示されていました。
以降は全て３０歳としてデータにしています。

#いざ解析
地道に集めたデータをPythonライブラリを用いて解析しました。

###特徴量
特徴量は入力項目としてあるうちの選りすぐりの以下を使用しました。

• ライク数
• 顔（顔が写っている写真かそうでないかの２値）
• 血液型
• 兄弟姉妹
• 学歴
• 学校名（入力があるかないかの２値）
• 職種
• 年収
• 身長
• 体型
• 結婚歴
• 子どもの有無
• 結婚に対する意思
• 子どもが欲しいか
• 家事・育児
• 出会うまでの希望
• 初回デート費用
• 社交性
• 同居人
• 休日
• お酒
• タバコ
• 名前_alpha（名前が全部アルファベットかそうでないかの２値）

この中のうち皆さんも気になるであろう特徴量とライク数の関係を見てみたいと思います。

####年収
いきなり来ました年収！
どうせ年収だろ！クッソ！
（年収上げたいのでデータサイエンス勉強してます１０００万ください）

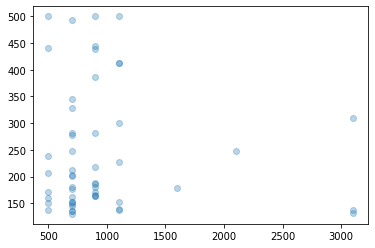
ということで、散布図を描いてみましょう。

import matplotlib.pyplot as plt
plt.scatter(data['年収'], data['いいね数'], alpha=0.3)
# dataはdataframeです。

(縦がライク数、横が年収)

【考察】
５００万ないやつは男ではない。月収１４万円さんなんてありえないです。
そう言われている気がします。

意外？なのは年収とライク数は相関があまり無いことです。
（高ければ高いほどライクが増えるわけではない）

実際に相関係数を出してみると...

pd.DataFrame({"x":data['年収'], "y":data['いいね数']}).corr()

年収xライクの相関係数

         x        y
x  1.00000 -0.06363
y -0.06363  1.00000

ほとんど相関関係は無いといえます。

ライクをたくさんもらっている人は年収だけじゃない何かがありそうです。
（*ただし５００万以上に限る）

他にどの特徴量が関係しているのでしょうか。どんどん見ていきましょう。

####学歴
学歴としての選択値には以下がありました。
　　短大/専門学校/高専卒 | 高校卒 | 大学卒 | 大学院卒 | その他

日本語だと扱いづらいので、

data['学歴'] = data['学歴'].replace({'短大/専門学校/高専卒':0 ,'高校卒':1 ,'大学卒':2 ,'大学院卒':3 ,'その他':4})

といった形でラベルエンコーディングを行いました。

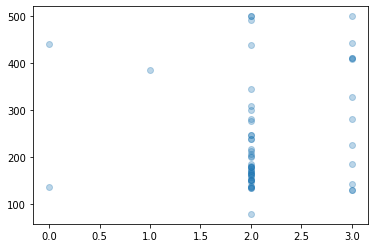
この形で散布図を描画して見ましょう。

plt.scatter(data['学歴'], data['いいね数'], alpha=0.3)

結果...

（目盛り調整してなくてすいません。）

'短大/専門学校/高専卒':0 ,'高校卒':1 ,'大学卒':2 ,'大学院卒':3 ,'その他':4
です。

大学以上がやっぱり多いですよねぇ。。。

ここで相関係数、、、ではなく、この場合は量的変数と質的変数の関係となるため、相関比を算出します。
学歴は数値化できない（大学卒と大学院卒はどれくらい差があるのかわからないので質的変数）ため、選択値毎にライク数の結果に偏りがあるかを調べてみます。

どこからかいただいて来た関数

def corr_ratio(x, y):
  variation = ((x - x.mean()) ** 2).sum()
  #print("    variation", variation)
  inter_class = sum([((x[y == i] - x[y == i].mean()) ** 2).sum() for i in np.unique(y)])
  #print("    inter_class", inter_class)
  return (inter_class / variation)

# 相関比を計算
corr_ratio(data.loc[:, ["いいね数"]].values, data.loc[:, ['学歴']].values)

結果

# 0.8820459777290447

それなりに相関がありそうですね。

【考察】
最低でも大学は出てた方がいいわね
そう言われている気がします。

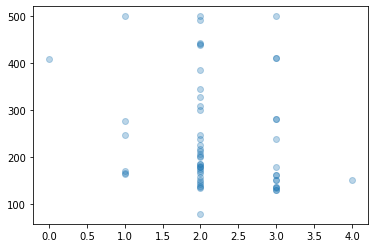
####身長
低くても許してくれるよね？
頼むから年収みたいなことにはならないで欲しい。。。

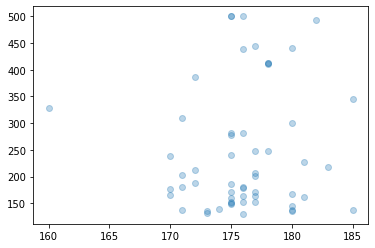
早速みてみましょう。

# NaNの行を除外してplot
plt.scatter(data.loc[data["身長"].notnull()]["身長"], data.loc[data["身長"].notnull()]['いいね数'], alpha=0.3)

...?

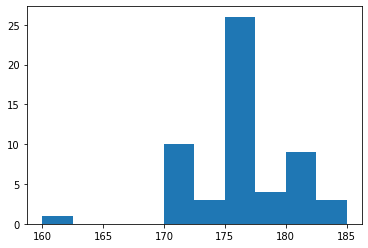
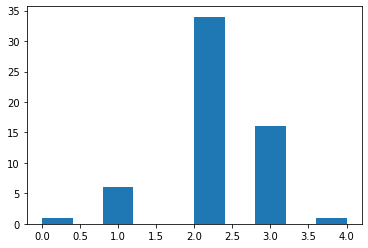
これだと身長の分布がわかりづらいので、ヒストグラムで出して見ましょう。

plt.hist(data["身長"].astype(np.float32))

(5cmで丸めてます。)

ちなみに日本人男性の平均身長は１７０cmくらいです...
容赦ないですね

ここでも相関係数を出して見ましょう。

pd.DataFrame({"x":data['身長'].astype(np.float32), "y":data['いいね数']}).corr()

身長xライクの相関係数

          x         y
x  1.000000  0.073241
y  0.073241  1.000000

こちらも相関関係はほとんどないですね。

【考察】
180cmとは言わないけど175cmは欲しいわ
そう言われている気がします。

私171cm...
○ねやマジで

####体型

体型の選択肢は以下です。
　　'スリム': 0, 'やや細め': 1, '普通': 2, '筋肉質': 3, 'ややぽっちゃり': 4, 'ぽっちゃり': 5

上記に置換した後でplotしてみます

# NaNの行を除外してplot
plt.scatter(data.loc[data["体型"].notnull()]["体型"], data.loc[data["体型"].notnull()]['ライク数'], alpha=0.3)

（またまた目盛り調整してなくてすいません。）

うーん、なんか正規分布っぽい、というか、体型が普通の人が一番多くて他が数的に少ないでしょうから、何も偏りがない様に見えます。

[2019/11/12 追記--]
ヒストグラムで出しなおしてみます。

plt.hist(data_original['体型'].astype(np.float32))

（目盛ｒｙ）

1番目に普通、2番目に筋肉質が多いですね。
[-- 2019/11/12 追記]

次に相関比を出しておきます。

# 相関比を計算
corr_ratio(data.loc[:, ["ライク数"]].values, data.loc[:, ['体型']].values)

結果

0.9457908220700801

結構な数字になりました。
データが少ないので正直信頼度は不明ですが、まぁ一番人数が多い普通か筋肉質がいいんでしょうね。

【考察】
普通か筋肉質がいいわ
目指せ普通体型

####ここら辺で...
みなさんの気になるところはだいたい見れたのではないでしょうか。
以降は機械学習を用いてライク数予想機を作ってみようと思います。

#ライク数予想機を作ってみる
##前処理
回帰を行うにあたってラベル処理は行いましたが、ほとんどの項目で数値とその重要性は比例しません。
例えば、先ほどの学歴の様に「その他」を４で置き換えたからといって、それが４より小さい３の「大学卒」より優れているというわけではありません。

ですので今回は頻度ラベリングを行いました。
頻度ラベリングに関してはここでは説明しませんが、頻度が多いほど大きい数字になります。
（ライク数の多い人が選ぶ選択肢はいいに違いないという仮説を考えると結構妥当かと思います。）

def labeling(data):
  for column in data.columns:
    #Likesは目的変数なので避ける。身長と年収はのちに標準化します。
    if not column in ['Likes', 'Heights', 'Salary']:
      #size of each category
      freq_encoding[column] = data.groupby(column).size()
      #get frequency of each category
      freq_encoding[column] = freq_encoding[column]/len(data)
      #print(encoding)
      data[column] = data[column].map(freq_encoding[column])
      freq_encoding[column] = freq_encoding[column].to_dict()
  return freq_encoding, data

# freq_encodingは今後の予想したいデータを頻度ラベリングする際に使い回す。
freq_encoding, data = labeling(data)

身長と年収は標準化しました。

def normalize(data):
  # #標準化
  # 身長：曰く171.5(平均)/5.8(標準偏差)らしい
  data['Heights'] = ((data['Heights']-171.5)/5.8)
  # 年収は標準偏差が得られず...
  data['Salary'] = ((data['Salary']-data['Salary'].mean())/data['Salary'].std())
  return data

data = normalize(data)

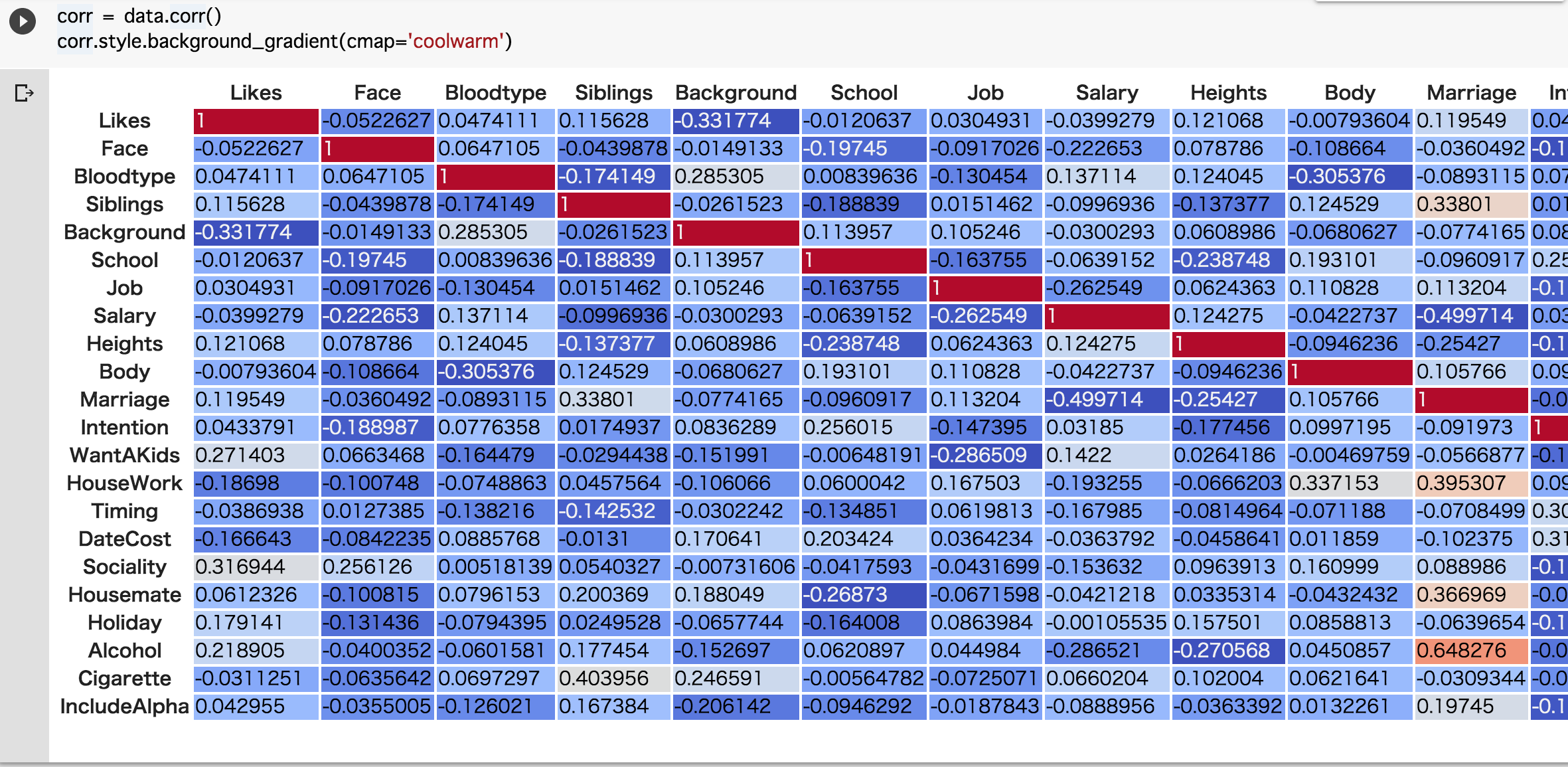
さてその上で、それぞれの特徴量とライク数の相関係数を出して見たいと思います。
この文脈で行くと、相関関係があるということは、強者が揃って選択している選択肢があるということですね。

どうでしょう。Likesの列(最初の列)を見てください。

・Background （学歴）
・WantAKids （子供が欲しいか）
・Sociality （社交性）
・Alcohol （お酒）
に多少の相関が見られます。（数値が１に近いほど相関がある）

要するにここら辺を強者の真似をすればライクが増えるかもしれませんね！！

##特徴量の選定
過程は端折りますが、色々な特徴量を抜いたりしたところ、下記の特徴量は含まないのが精度が一番良かったです。

・顔の有無
・体型
・年収

相関比/相関係数が低い物を削ればいいわけでもなかったので、特徴量の削減というのは実際に試すしかないんでしょうかね。

というか体型と年収はライク数には関係がないっていうのは結構意外ですね。
（但し、年収500万以上に限るということを忘れるなよ！）

[2019/11/14 追記--]
【謝罪】
顔の有無に関してですが、"1枚目に顔が判別できるほど写っているか"というフラグであるのが実際です。（画像は複数枚登録できるのを忘れていました。）
ですので、顔が関係ないという話ではありません。
[-- 2019/11/14 追記]

##モデルの選定
今回は機械学習の勉強ということで深層学習は用いませんでした。
線形回帰（ノーマル・Lasso・Ridge）、決定回帰木、SVRを試したところ、SVRが一番マシでした。

また、このデータセットが少ない中ではあまりやってはいけないと言われているホールドアウト法でですが、約83％の精度を出すことができました。

過適合が考えられますが、あまり時間をかけても仕方がないので、この精度で進めます。

[2019/11/12 追記 --]
ちなみにtrainとtestは約８：２です。
[-- 2019/11/12 追記]

##自分のライク数を予想してみた
１ヶ月も立たずにやめてしまいましたが、私のライク数は約80でした（トホホ...

そんな私のデータを正しく予想できるのかやって見ました。

私のデータは以下です。

my_df = pd.DataFrame({
  'ライク数': 80.0,
  '顔': 'あり',
  '血液型': 'O型',
  '兄弟姉妹': '長男',
  '学歴': '大学卒',
  '学校名': 'なし',
  '職種': 'IT関連', #2019/11/11 試しに会社員にしてたのを忘れてました。
  '年収': '***',  # 年収は関係ないので秘密
  '身長': '171',
  '体型': '普通',
  '結婚歴': '独身（未婚）',
  '結婚に対する意思': '良い人がいればしたい',
  '子どもが欲しいか': 'わからない',
  '家事・育児': '積極的に参加したい',
  '出会うまでの希望': '気が合えば会いたい',
  '初回デート費用': '男性が全て払う',
  '社交性': '少人数が好き',
  '同居人': '一人暮らし',
  '休日': '土日',
  'お酒': '飲む',
  'タバコ': '吸わない',
  '名前_alpha': 0
}, index=[0])

##以下ラベルエンコーディングしたり頻度エンコーディングしたり...

# ライク数は落としてnumpyに変換
X = my_df.iloc[:, 1:].values 

# いざ予想！！！！
print(model_svr_rbf1.predict(X))

結果

[73.22405579]

遠からずな数字出してんじゃねぇよ!!!!（っていうか機械学習しゅごい）

（2019/11/11: 試しに職種を会社員にしてたのを忘れてました（結果：64ライクくらい）。当時の入力であるIT関連に直しました。IT関連の方が好印象！？）

ちなみに、この後自分の値も入れて学習させたら（全体の）精度が上がったんで（約83→86%）私のもらったライクは妥当な数字だったという可能性が大いにあります（涙

##データを変えて遊んでみた
###大学院卒にしてみた

...
  '学歴': '大学院卒', #大学卒から変更
...

# 結果
[207.56731856]

おそるべし学歴。

###身長180cmにしてみた

...
  '身長': '180', #171から変更
...

# 結果
[164.67592949]

おそるべし身長。

#最後に
約86%というぼちぼちな精度で予想機が出来てしまいました。
これはつまり選択肢でライク数は変わるということではないでしょうか。

そして、年収（500万～であれば）と体型（私は普通体型ですが）は関係ありませんでした。
つまり私が選択した選択肢に上がらない要因があった可能性があります。

結果を踏まえて、年収はあまり関係ないみたいなので今後は身長を伸ばす事を頑張ろうと思います(違