#はじめに#
この記事はLinkbal_Advent_Calendar_2020の12日目の記事です。
この数年間、人工知能(Artificial Intelligence、略称：AI)の言葉って所々でもよく聞くはずですね。簡単に目的を言えば機械が自身で学習して自ら賢くなることも間違うわけではありません。
人工知能の週類はいくつかありますが、大学時代にちょっと調べたことがあって面白い感じがしたのは進化的計算です。
生物学から浮かばれた手法で、ある問題の最高解決策を進化や突然変異を適用して求めることです。この手法は遺伝的アルゴリズムと群知能に分類される。今日は遺伝的アルゴリズム(Genetic Algorithm、略称：GA)の概要についてザッと紹介させていただきます！
#概要#
遺伝的アルゴリズムはダーウィン(Darwin)の進化論に基づき、生物突然変異や交叉や選択などを使って最適化または検索問題に対する高品質の解決策を調べるために使用されています。
では、何が進化論に基づくか遺伝的操作がどうやって真似して取り込むかこれから以下のように簡単に説明します。
#アルゴリズムの流れと主な要因#
##流れの省略##
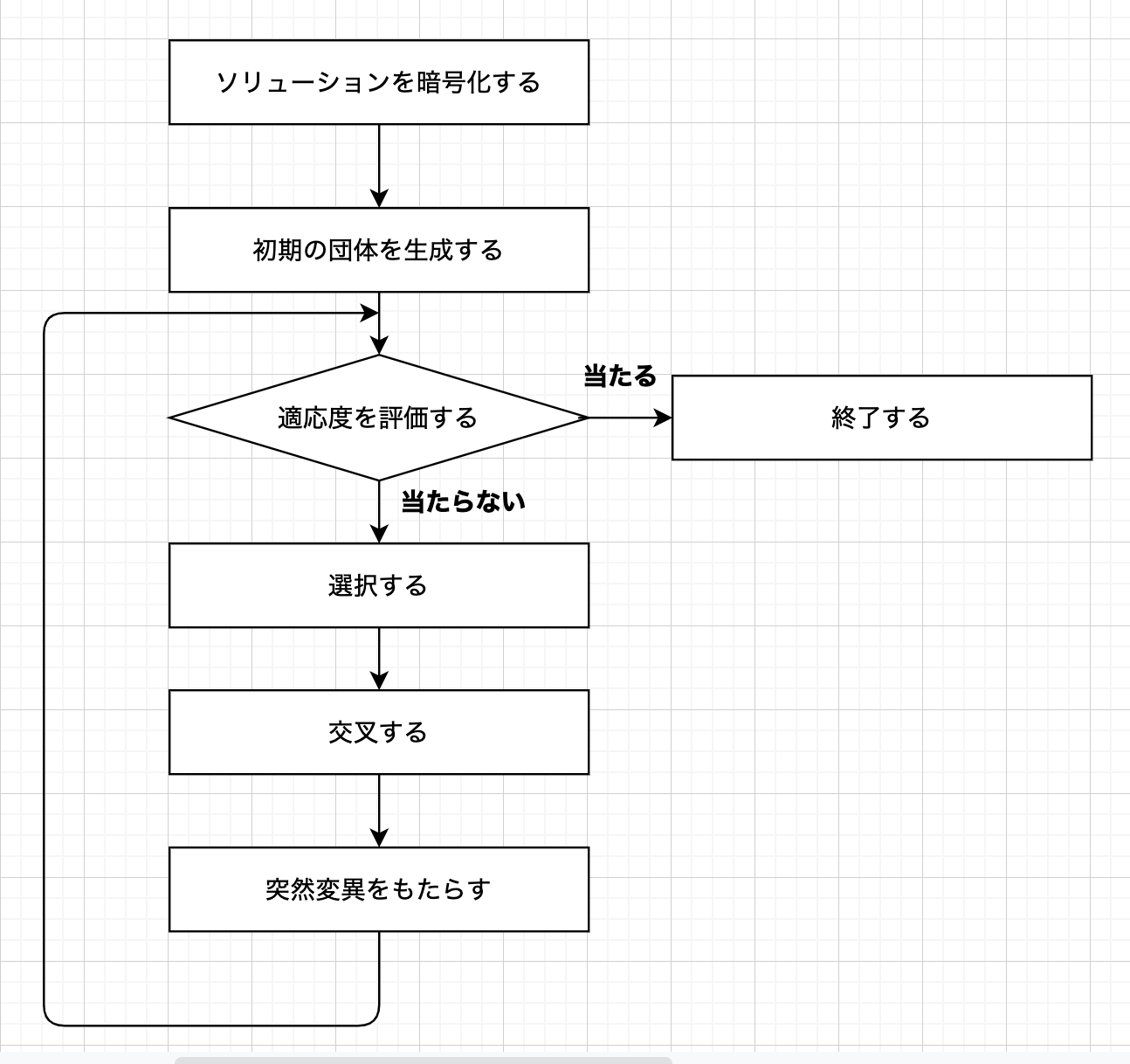
アプローチはいくつかあってもまとめておけばこの流れのようになります。四つあります！
- 問題の答えを暗号化する（バイナリー変換するとか置換するとか）
- 以上のソリューションを個体として初期の団体を生成する（N個体）
- 適応評価を計算して遺伝的数学を使って新しい個体を生成する
- 望みたい結果に近づかないとまた先ほど作られた個体で次世代を作り、それから繰り返す
##主な要因の概要##
###選択###
選択は生物の自然淘汰説を基づいて、適応度で判断して個体を増やすか削除するかの操作です。 選択のアルゴリズムはたくさんありますのでもっともわかりやすいのを紹介します。
ルーレット選択
ルーレット選択は個体 $i$ を選ぶ確率を $p_i$ と置いたとき、
$p_i = \frac{f_i}{\sum_{k=1}^N f_k}$ （$f_i$は個体の適応度である）
とする選択方式です。と言うと $f_i$ は個体 $i$ の適応度を表示する。見るとわかるはずなのは最も適度が高い個体は大分次世代に変遷できることです。しかし、適応度が高いことが前提になると最小値を求める問題なら使いづらいと分かられています。さらに、もしかしたら個体間の適応度の格差が激しい場合は非常に選ばれるのは適応度の高い個体なって、初期収束になってしまいます（全部同じ個体）。
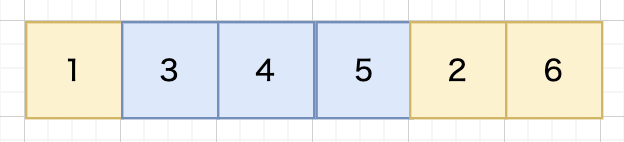
トーナメント選択
トーナメント選択は決めた数（トーナメントサイズ）だけ集団の中からランダムで個体を取り出してその中から最も適応度の高い個体を選択する方式です。トーナメントサイズを変更すると選択圧を変更できる特徴があります。だが、サイズを大きくしたら選択圧を高めることができても初期収束による局所的な最適解に陥りやすくなってしまします。
###交叉###
交叉は生物が交配によって子孫を残すことをモデル化したもので、個体の遺伝子の一部を入れ換える操作です。すなわち、最も重要な遺伝的操作と言うこともできます。切る数は $X$ なら $X$ 点交叉と言われます。
一点交叉
切れた部分を交換することです。
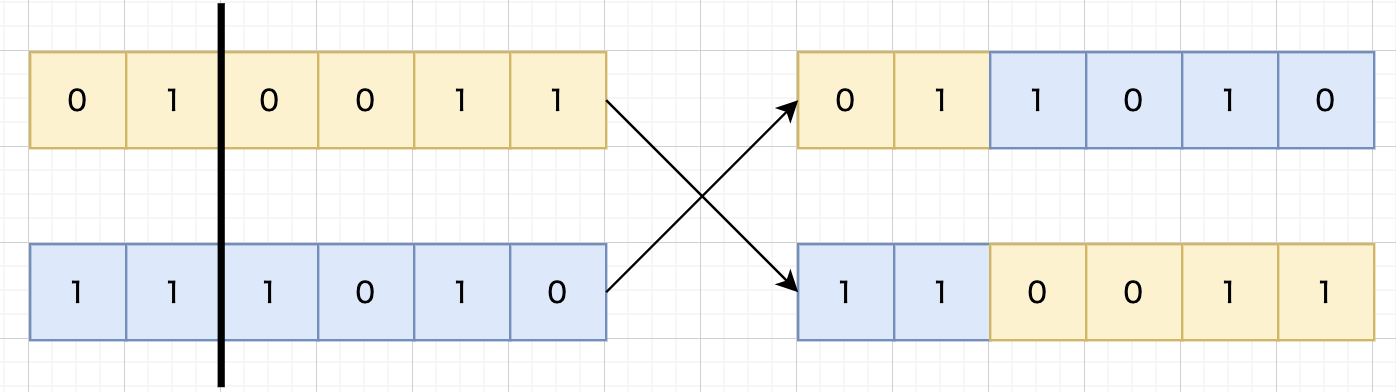
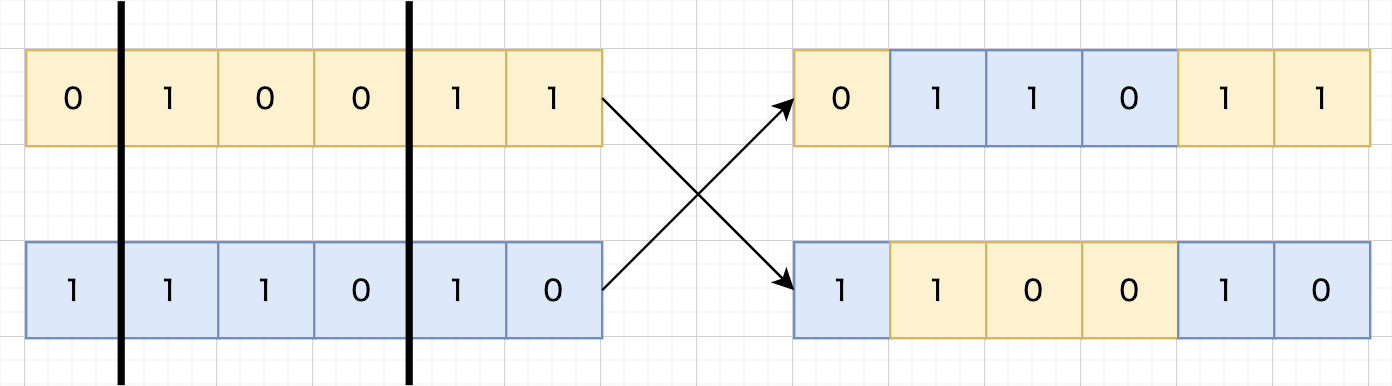
二点交叉
二つの交叉点に挟まれている部分を入れ換えるということです。
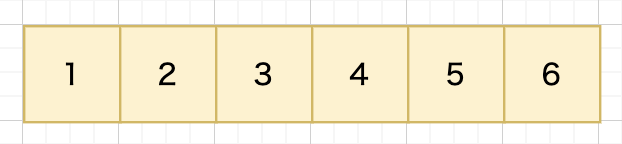
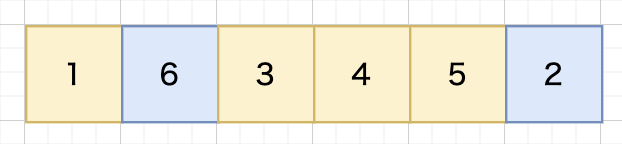
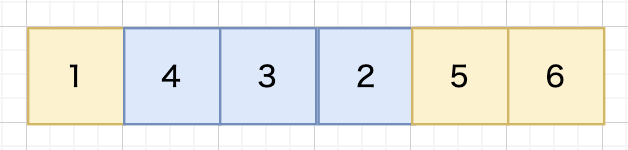
###突然変異###
突然変異は生物に見られる遺伝子の突然変異をモデル化したもので、個体の遺伝子の一部を一括変化させる操作です。局所的な最適解に陥ることを防ぐ効果があるのため実装されてます。
注意すべき点は突然変異の確率は0.1%~1%です。なぜかというと、確率が低すぎると局所的な最適解に陥りやすくなりますが、高すぎるとランダム探索に近づいてしまうからです。
元々
交える突然変異
個体の中に二つの部分を変換します。
逆にする突然変異
個体の一部の中に逆順にします。
変異する突然変異
個体の一部を別の位置に変異します。
#終わりに#
ここでは以上ですが、よかったら次の記事で例を上げたいと思ってます。単なる概要ですが、みなさんに遺伝的アルゴリズムについての興味をもたらしますでしょうか。とっても詳しいとは言えないですので間違ったところを見つければ是非ご意見いただきたくと幸いです。