今回は、Scalaの末尾再帰について書いていきたいと思います。大学では型理論とかを学んだわけじゃないので割とそこらへんは雑です。
最近、再帰ロジックをプロダクションコードに導入するのが個人的に流行っているので、こういうテーマを選択しました。Scalaに関する末尾再帰の記事はそこそこ既に出揃っており、Scalaとして特に目新しいことは全く無いと思います。各セクションの下部、もしくは途中に参考資料のリンクを張っています。また、最下部に、全ての参考資料をまとめています。
なぜ再帰で書くべきか
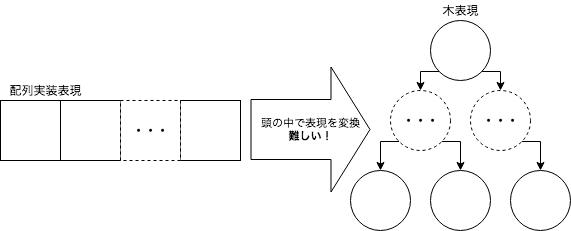
ツリーのような複雑な再帰データ構造は、メモリ効率の良い配列実装が一般的になっています。しかし人間からしてみると、配列内部の状態と実際に構築されているツリーのイメージを結びつけることが困難です。
そのためメモリ要件に特に厳しい制約が存在しない場合は、人間のイメージをできる限りそのまま表現したオブジェクトチェーンによるツリー構造をデザインした方が、ロジックの可読性を高めることができると考えられます。
再帰的データ型を用いることで、配列実装のデータ型を用いる時と比べ、以下のようなメリットを得ることができます(個人的感想)。
-
無制限なジャンプを制限する
-
whileループを用いるようなジャンプ制御は、無制限なジャンプを可能にします。無制限なジャンプを使用したランダムアクセスが発生すると、存在しない値へのアクセス(ArrayIndexOutOfRange)や、意図しない制御への遷移など、バグの温床になります。)
-
-
再帰関数のロジックは直感的にわかりやすい
-
whileループを用いるようなジャンプ制御では、カウンタ変数(例えば変数i,jのような)を導入して処理を行う。しかしカウンタ変数を用いたロジックは、本質的ではないのでわかりずらい。再帰ロジックであれば、思考をダイレクトに反映したロジックを記述しやすい。
-
ソフトウェア開発の現場では、再帰ロジックが使われることはあまり無いような気がします。弊社でも積極的に再帰を使用したロジックの記述はあまり見たことがありません。
しかし、リストやツリーをはじめとする再帰的データ型に対して、whileループのようなジャンプ制御を用いるより、再帰ロジックを用いた方がシンプルな記述になることが多いはずです。
しかし、再帰呼び出しは下手な実装を行ってしまうと、コールスタックを消費することによるスタックオーバーフローやメモリ不足を引き起こしてしまう可能性があります。
高い可用性が必須なプロダクション環境で、このようなエラーを発生させるロジックを採用することは危険を招きます。
そのため、再帰呼び出しをジャンプ制御に変換することができる末尾再帰パターンで記述される末尾再帰関数を実装する必要があります。
末尾再帰とは
Wikipediaによれば、
末尾再帰(まつびさいき)とは、再帰的な関数やプロシージャにおいて、自身の再帰呼び出しが、その計算における最後のステップになっているような再帰のパターンのことである。再帰にかかわらず一般に、そのような最後の呼び出しを末尾呼び出し (en:Tail call)という。呼び出しではなく、戻り先を保存しないジャンプに最適化できるという特徴がある(#末尾呼出し最適化)。
ある関数が関数を呼び出す時、一般に呼び出し元と呼び出し先の両方の状態を保持する必要があるので、この情報をコールスタックに積んでいかなければなりません。これは再帰呼び出しでなくても再帰呼び出しでも変わらない点です。
再帰関数はwhileのようなジャンプ制御ではなく、関数内部で自分自身を再帰的に呼び出すことでループを表現します。その特性上、自分自身を大量に呼び出す必要があるケースが少なくありません。再帰呼び出しでもコールスタックを積んでいくので、メモリを消費してしまいスタックオーバーフローやメモリ不足に陥ることがあります。
再帰関数を、末尾再帰と呼ばれる再帰パターンで記述することで、言語によっては最適化を行えます。この最適化によって、コールスタックを消費する関数呼び出しではなく、ジャンプ制御に変換されます。ジャンプ制御に変換されることで、処理が高速になったり、スタックオーバーフローやメモリ不足に陥ることを防ぐことができます。
Scalaにおける再帰と末尾再帰
では、Scalaにおける再帰と末尾再帰についてみていきましょう。
Scalaで再帰を使うべき理由
配列などを用いた木構造の実装は非常にメモリ効率の良いものになりますが、前述したように実装理解が難しいと考えられます。また、配列を用いている以上、後の機能の追加や振る舞いの変更に対応しづらいかもしれません。
Scalaはオブジェクト指向と関数型のパラダイムを併せ持つ言語です。
そのため、豊かな表現力を持ったオブジェクトと、強力なパターンマッチであるmatch-case式を用いた可読性の高い再帰関数を実装することが容易です。
Scalaでの末尾最適化
Scalaにおいても末尾再帰で書かれた再帰関数は、コンパイラによって最適化がかかり、最終的にジャンプ制御に変換してくれます。実際には、whileループに変換されるようです。
Scalaには@scala.annotation.tailrecというアノテーションが用意されており、このアノテーションを付与したメソッドは、コンパイル時に末尾再帰かどうかをチェックしてくれます。もしこのアノテーションを付与したメソッドが末尾再帰の形になっていなければ、コンパイル時にエラーになり、最適化がかかっているか、かかっていないかを確認することができます。また、Intellijではコンパイルせずとも末尾再帰になっているかなっていないかをチェックする機能があり、大変便利です。
Scalaでは、再帰関数はrecursiveやgoという単純な名前のローカルメソッドとして定義されることが多いようです。ローカルメソッドであれば、メソッド内で閉じた名前空間が生成され、他のメソッドでrecursiveやgoという名前が衝突することもありませんし、ローカルメソッドはコンパイル時にクラス内のprivate finalなメソッドとして定義されるようなので、呼び出しの度に関数定義が評価されるということはありません。
以下によく使う末尾再帰をロジックに使うメソッドの例を示します。
def f(...): T = {
@scala.annotation.tailrec
def recursive(...): T = {
???
}
recursive(...)
}
末尾最適化されない再帰
残念ながら、Scalaでは末尾最適化できない末尾再帰パターンも存在します。
ここからは、末尾最適化できない2つの再帰を紹介します。
末尾相互再帰
相互再帰は、複数の関数がお互いを再帰呼び出ししている形式の再帰です。
相互再帰を構成する関数が二つだけの場合は以下のようになります。
def f(...): T = {
def foo(...): T = {
??? // 最後の計算ステップがfooの呼び出しもしくはbarの呼び出し
}
def bar(...): T = {
??? // 最後の計算ステップがbarの呼び出しもしくはforの呼び出し
}
// fooもしくはbarの呼び出し
}
しかし、fooの関数内の最後の計算ステップで自分自身が呼び出されないので、Scalaでは末尾最適化を行うことができません。
継続渡しスタイルの再帰
And/Or条件式を模した以下の多分木を、複数のAnd条件の線形リストに分解するようなロジックを考えましょう。
sealed trait Cond[T]
final case class And[T](conds: Cond[T]*) extends Cond[T]
final case class Or[T](conds: Cond[T]*) extends Cond[T]
final case class Elem[T](value: T) extends Cond[T]
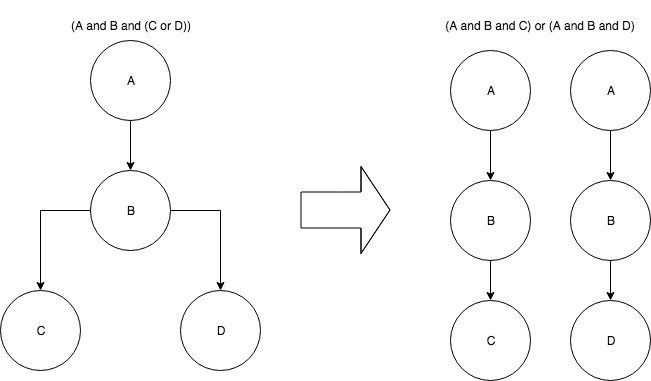
And/Or条件式の多分木は、以下のようにして複数の線形リストに分解することが可能です。
これは、どのような条件式でも以下の形に分解できるということです。
(値 and 値 [and 値]*) (or (値 and 値 [and 値]*))*
入力に対する出力サンプルは以下のようになっています。
val cond = And[Int](
Elem[Int](1),
And[Int](
Elem[Int](2),
And[Int](
Elem[Int](5),
Elem[Int](6)),
Elem[Int](7)),
And[Int](
Elem[Int](3),
Elem[Int](4)))
scala> Cond.recursive(cond)
res: List[List[Int]] = List(List(1, 2, 5, 6, 7, 3, 4))
val cond = And[Int](
Elem[Int](1),
Or[Int](
Elem[Int](2),
And[Int](
Or[Int](
And[Int](Elem(10), Elem(11), Elem(21)),
And[Int](Elem(32), Elem(9), Elem(12)),
Elem(14)),
Elem[Int](6)),
Elem[Int](7)),
And[Int](
Elem[Int](3),
Elem[Int](4)))
scala> Cond.recursive(cond)
res: List[List[Int]] = List(List(1, 2, 3, 4), List(1, 10, 11, 21, 6, 3, 4), List(1, 32, 9, 12, 6, 3, 4), List(1, 14, 6, 3, 4), List(1, 7, 3, 4))
まずは通常の再帰での実装を見ていきましょう。
object Cond {
def recursive[T](cond: Cond[T]): List[List[T]] =
cond match {
case And(Elem(value)) => (value :: Nil) :: Nil
case And(cond: Cond[T]) => recursive(cond)
case And(Elem(value), conds @ _*) =>
recursive(And(conds: _*)) map (value :: _)
case And(cond: Cond[T], conds @ _*) =>
for {
headExpr <- recursive(cond)
tailExpr <- recursive(And(conds: _*))
} yield headExpr ++ tailExpr
case Or(Elem(value)) => (value :: Nil) :: Nil
case Or(cond: Cond[T]) => recursive(cond)
case Or(Elem(value), conds @ _*) =>
(value :: Nil) :: recursive(Or(conds: _*))
case Or(cond: Cond[T], conds @ _*) =>
recursive(cond) ++ recursive(Or(conds: _*))
}
}
通常の再帰の実装ではrecursive(And(conds: _*)) map (value :: _)をはじめとする複数箇所で、末尾呼び出しが自分自身になっていないため、@tailrecアノテーションを付けるとコンパイルエラーが発生します。
そこで、継続渡しスタイルと呼ばれる再帰関数の手法を用いることにしましょう。継続渡しスタイルは、今現在の関数呼び出しの中で、次の再帰呼び出しの結果に対する処理を記述した「継続」を渡すものです。
単に値を次の再帰呼び出しに渡すようなアキュムレーターとは異なり、関数を渡すことになります。
継続渡しスタイルに書き直した実装は以下になります。
object Cond {
def recursive[T](cond: Cond[T], cont: List[List[T]] => List[List[T]]): List[List[T]] =
cond match {
case And(Elem(value)) => cont((value :: Nil) :: Nil)
case And(cond: Cond[T]) =>
recursive(cond, (stacks: List[List[T]]) => cont(stacks))
case And(Elem(value), conds @ _*) =>
recursive(
And(conds: _*),
(stacks: List[List[T]]) => cont(stacks map (value :: _)))
case And(cond: Cond[T], conds @ _*) =>
recursive(
cond,
(headStacks: List[List[T]]) => {
val concatExpr = for {
headExpr <- headStacks
tailExpr <-
recursive(
And(conds: _*),
(tailStacks: List[List[T]]) => tailStacks)
} yield headExpr ++ tailExpr
cont(concatExpr)
}
)
case Or(Elem(value)) => cont((value :: Nil) :: Nil)
case Or(cond: Cond[T]) =>
recursive(cond, (stacks: List[List[T]]) => cont(stacks))
case Or(Elem(value), conds @ _*) =>
recursive(
Or(conds: _*),
(stacks: List[List[T]]) => cont((value :: Nil) :: stacks))
case Or(cond: Cond[T], conds @ _*) =>
recursive(
cond,
(headStacks: List[List[T]]) => {
val tailStacks =
recursive(
Or(conds: _*),
(tailStacks: List[List[T]]) => tailStacks)
cont(headStacks ++ tailStacks)
}
)
}
}
末尾関数呼び出しが全て自分自身になっていることが確認できます。
しかし、@tailrecアノテーションを付けるとコンパイルエラーになってしまいます。Haskellなどの言語では、継続渡しスタイルは末尾最適化されるそうなのですが、Scalaと継続渡しスタイルは相性が悪いようで末尾最適化を行うことができないようです。
トランポリン化による末尾最適化
「末尾最適化されない再帰」では、末尾相互再帰と、継続渡しスタイルの再帰があることを紹介しました。しかし、トランポリン化と呼ばれる方法によって、標準では最適化ができなかった末尾再帰であっても最適化可能になります。トランポリン化自体の詳細についてはあまりわからないので、以下に参考資料を載せておきます。
Scalaでトランポリン化を使って末尾再帰最適化を行うには、scala.util.control.TailCallsを使う必要があります。
使用例は公式ドキュメントに載ってます。Stackless Scala With Free Monadsという論文に基づいた実装がなされており、スタックレスな末尾再帰を記述することが可能になっているみたいです。
注意すべきは、このトランポリン化によって行う末尾最適化というのはScalaがコンパイル時に「whileループに自動的に変換してくれるようにする」のではなく、「既にスタックレスな再帰が記述できている」ということです。ですので、トランポリン化したスタックレス再帰は@scala.annotation.tailrecアノテーションを付与すれば分かると思いますが、Scalaはそれが末尾最適化可能であるということを認識できていません
末尾相互再帰
末尾相互再帰の場合でも同様にスタックレス再帰として記述することが可能です。
def f(...): T = {
def foo(...): TailRec[T] = {
??? // 最後の計算ステップがfooの呼び出しもしくはbarの呼び出し
}
def bar(...): TailRec[T] = {
??? // 最後の計算ステップがbarの呼び出しもしくはforの呼び出し
}
// (fooもしくはbarの呼び出し).result
}
継続渡しスタイルの再帰
継続渡しスタイルの再帰は、トランポリン化を使うことで継続渡しスタイルではない形式で記述することができます。再帰呼び出しの結果をmapやflatMapなどを使って扱うことができます。
object Cond {
import scala.util.control.TailCalls._
def recursive[T](cond: Cond[T]): TailRec[List[List[T]]] =
cond match {
case And(Elem(value)) => done((value :: Nil) :: Nil)
case And(cond: Cond[T]) =>
tailcall { recursive(cond) }
case And(Elem(value), conds @ _*) =>
tailcall { recursive(And(conds: _*)) } map { exprs =>
exprs map (value :: _)
}
case And(cond: Cond[T], conds @ _*) =>
for {
headExprs <- tailcall { recursive(cond) }
tailExprs <- tailcall { recursive(And(conds: _*)) }
} yield for {
headExpr <- headExprs
tailExpr <- tailExprs
} yield headExpr ++ tailExpr
case Or(Elem(value)) => done((value :: Nil) :: Nil)
case Or(cond: Cond[T]) =>
tailcall { recursive(cond) }
case Or(Elem(value), conds @ _*) =>
tailcall { recursive(Or(conds: _*)) } map { exprs =>
(value :: Nil) :: exprs
}
case Or(cond: Cond[T], conds @ _*) =>
for {
leftExprs <- tailcall { recursive(cond) }
rightExprs <- tailcall { recursive(Or(conds: _*)) }
} yield leftExprs ++ rightExprs
}
}
トランポリン化によって記述されたスタックレス再帰は、通常の再帰で書かれた場合とよく似ているのがわかります。トランポリン化によって変わったのが、再帰呼び出しの結果がTailRec[T]でラップされているぐらいなので、通常の再帰で書いた場合とあまり変わりません。
まとめ
一般的な末尾再帰、再帰的データ型のメリット、Scalaにおける再帰、末尾最適化、末尾最適化できない再帰、トランポリン化によるスタックレス再帰について色々書きました。
簡単な再帰ロジックであれば、アキュムレータを使用することで、コンパイラによる末尾最適化の恩恵を受けることができます。実際コンパイラによる末尾最適化は、whileへの変換なので、速度的な面でいうと@tailrecできちんと末尾再帰として認識される再帰ロジックを記述した方が好ましいと考えられます。
実際、トランポリン化とアキュムレータの性能比較で計測された結果によれば、常にアキュムレータを使用した方がトランポリン化よりかは高速のようです。