はじめに
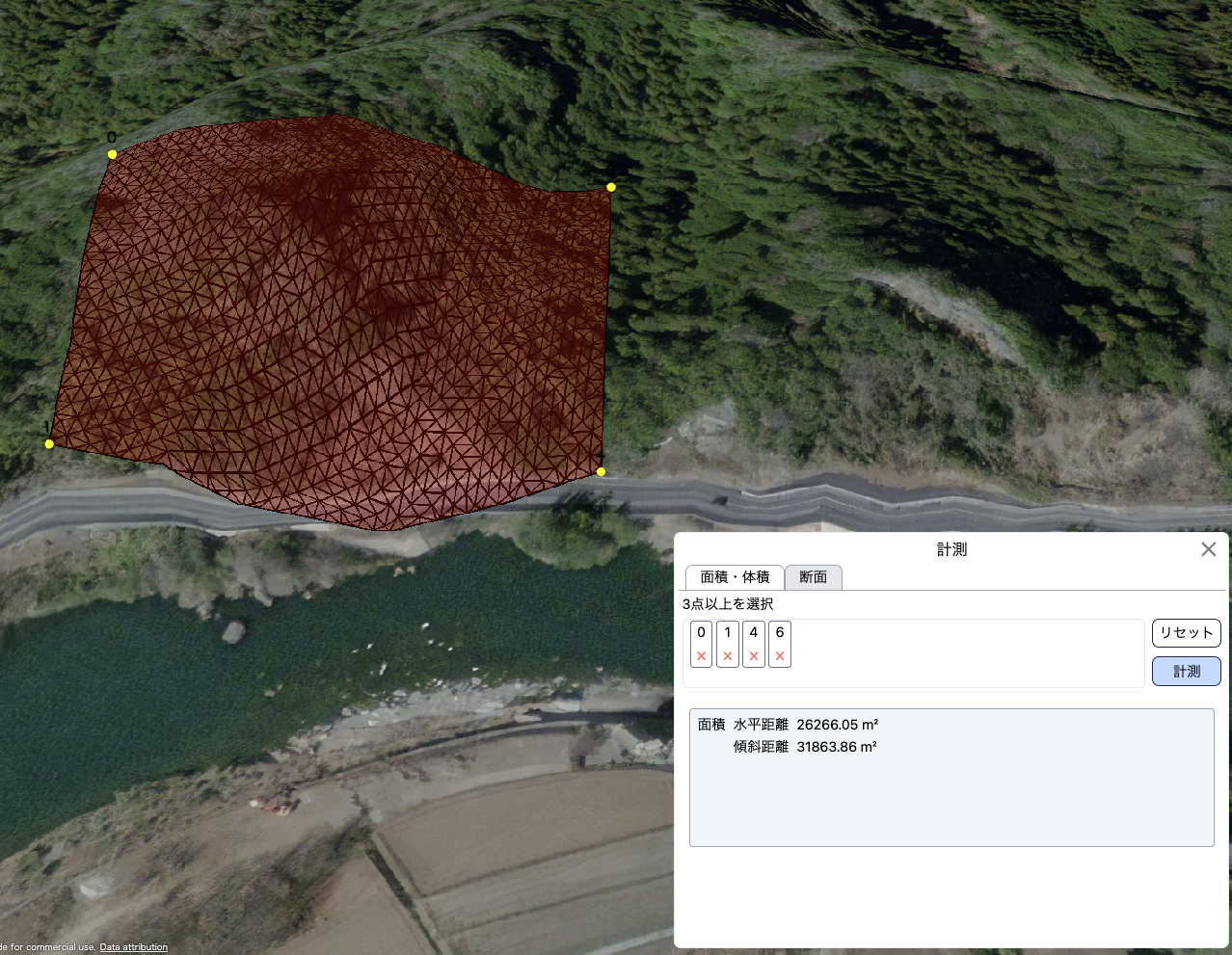
Cesiumで指定したポリゴンの地形の表面積をフロントのみで算出してみた。
イメージ
処理の概要
処理としては、指定したポリゴンを三角形に分割し、それぞれの面積を合計することで表面積を求めている
- 計測対象のポリゴンを指定する(説明は省略
- ポリゴンの中に等間隔にポイントをプロットする
- 等間隔のポイントをもとに三角グリッドを作成する
- 三角形の3辺の高さを考慮した長さを算出する
- ヘロンの公式で面積計算
- すべての三角形の面積を合算して、ポリゴンの表面積を算出する
ヘロンの公式
3辺の長さから三角形の面積を求められる公式
$$
S=\sqrt{s(s-a)(s-b)(s-c)}
$$
ただし
$$
s=\frac{a+b+c}{2}
$$
2. ポリゴンの中に等間隔にポイントをプロットする
ポリゴンの中に等間隔にポイントをプロットするにはTurf.jsの「pointGrid」を使用した。
ポリゴンのBBOX内に等間隔にポイントをプロットし、当該ポリゴンでマスクをすることで、指定したエリアのみにプロットできる。
const gridPoints = pointGrid(bbox(targetPolygon), 0.005, {
units: 'kilometers',
mask: targetPolygon
})
ここでは5m間隔で指定したポリゴン(targetPolygon)内にポイントをプロットしている。
得られた結果
このままでは、境界部に間が空いているため、ポリゴンの頂点間に等間隔のポイントをプロットした。
これはTurf.jsのlineChunkを使用した。
// 頂点のポイント線分の等分のポイントを作成
const dividedPoints: Array<Array<number>> = [];
// 頂点でループ
Object.values(cartographicPoints).forEach((point, index: number) => {
const nextIndex = (index + 1) % Object.values(cartographicPoints).length;
// 頂点間の線分
const line = lineString([point, Object.values(cartographicPoints)[nextIndex]]);
// 頂点間の線分を分割した線分の終点を取得
lineChunk(line, 0.005, { units: 'kilometers' }).features.forEach((feature) => {
dividedPoints.push(feature.geometry.coordinates[1]);
});
});
ここでは、頂点の線分をループで回し、lineChunkで0.5mづつの線分に分割、その終点を等間隔なポイントとして取得している。
ポリゴン内の等間隔の点と境界部の等間隔の点を結合させると以下のような結果が得られる。
3. 等間隔のポイントをもとに三角グリッドを作成する
等間隔の点から三角グリッドを作成するのは、Turf.jsのtinを使用する。
// 三角形分割
const triangles = tin(allPoints);
ここではすべての等間隔の点を引数に、それらを繋げた三角形のリストを取得している。
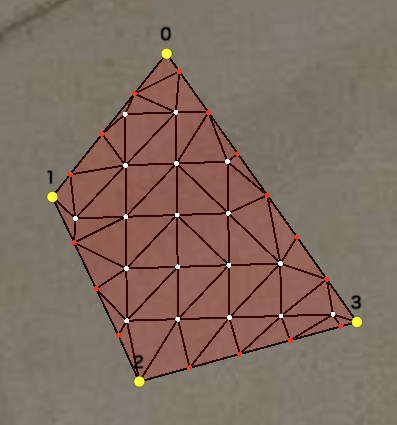
実行すると以下のような結果が得られる。
一方で、tinは近傍の点をつなげるので、へっこんでいる場合にはポリゴン外に三角形ができる。
これは生成された三角形のうち、重心がポリゴン内にあるもののみに絞り込めば良い。
// 重心がポリゴン内にある三角形のみ抽出
const filteredTriangles: Feature<Polygon, GeoJsonProperties>[] = triangles.features.filter(
(triangle) => {
const trianglePolygon = polygon([triangle.geometry.coordinates[0]]);
const centroidPoint = centroid(trianglePolygon);
return booleanWithin(centroidPoint, targetPolygon);
}
);
ここでは各三角形の重心を求め、Turf.jsのbooleanWithinで当該ポリゴン内に存在するかの確認をしている。
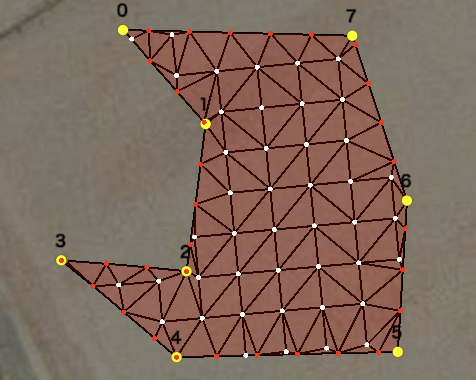
このように絞り込むことで以下のようにへっこんでいるポリゴンについても三角グリッドが正常に生成されることが確認できる。
4. 三角形の3辺の高さを考慮した長さを算出する
まずは標高を取得する。
標高の取得にはCesiumのsampleTerrainMostDetailedを使用することで、取得可能な最も細かい標高を取得することができる。
// 経緯度からCartographicインスタンスを生成
const cartographicPoint = Cartographic.fromDegrees(point[0], point[1]);
// sampledPoint.heightに標高が格納されている
const [sampledPoint] = await sampleTerrainMostDetailed(terrainProvider, [
cartographicPoint
]);
ただし、これは使用する地形データの3D Tilesにavailability(エリアとズームレベルの関係性)が定義されていない場合は使用することはできない。なので、sampleTerrainで再起的に高いズームレベルの標高を取得する必要がある。
例えば、手元に手軽な3D Tilesがなく、シームレス標高タイルを産総研の「NumericalPngTerrainProvider & ExtendedNumericalPngTerrainProvider」を使用してCesiumに描画している場合に発生する。
サンプルコード
function getElevationAtZoomLevel(
terrainProvider: CesiumTerrain, // 対象地形
zoomLevel: number, // ズームレベル
cartographic: Cartographic // Cartographic形式の座標
): Promise<number | undefined> {
return sampleTerrain(terrainProvider as unknown as TerrainProvider, zoomLevel, [cartographic])
.then((updatedCartographics: Cartographic[]) => {
const elevation = updatedCartographics[0]?.height;
// 標高が取得できた場合はその値を返す
if (elevation !== undefined && elevation !== 0) {
return elevation;
}
// 標高が0またはundefinedの場合、ズームレベルを下げて再試行
if (zoomLevel > 0) {
return getElevationAtZoomLevel(terrainProvider, zoomLevel - 1, cartographic);
}
// 最低ズームレベルでも標高が取得できない場合はundefinedを返す
return elevation === 0 ? 0 : undefined;
})
.catch((error) => {
console.error('Error sampling terrain:', error);
return undefined;
});
}
このように取得した標高から、ポイントの2点間の距離をピタゴラスの定理を使用して求める
// 水平距離
const horizontalDistance = distance(point1, point2, { units: 'kilometers' }) * 1000;
// 垂直距離
const heightDifference = Math.abs(elevation1 - elevation2);
// 斜距離
const slopeDistance = Math.sqrt(
horizontalDistance * horizontalDistance + heightDifference * heightDifference
);
このようにすることで、各三角形の3辺の長さを取得することができる。
ここでグリッドを確認してみよう。
1つの頂点を複数の三角形が共有していることがわかる。また辺についても同じだ。
頂点の取得、また辺の算出はダブりがあるのでキャッシュをさせることでより、効率的かつ無駄のない処理が実現できる。
またループで処理を回すのは時間がかかるので、非同期で行うのが好ましい。
const elevationCache = new Map<string, number>();
// 標高を取得する関数
async function getElevation(point: number[]) {
// elevationCacheを使用して標高を取得
const key = point.map((coord) => coord.toFixed(7)).join(',');
if (elevationCache.has(key)) {
// キャッシュに存在
return elevationCache.get(key);
} else {
// キャッシュに存在しない
const cartographicPoint = Cartographic.fromDegrees(point[0], point[1]);
const [sampledPoint] = await sampleTerrainMostDetailed(terrainProvider, [
cartographicPoint
]);
elevationCache.set(key, sampledPoint.height);
return sampledPoint.height;
}
}
// 全ての標高を並行して取得
const elevationPromises = dividedTriangles.map(async (triangle) => {
const coordinates = triangle.geometry.coordinates[0];
const elevations = await Promise.all(
[coordinates[0], coordinates[1], coordinates[2]].map(getElevation)
);
return { coordinates, elevations };
});
ここでは頂点の座標をキーとし、キャッシュに存在しない場合は取得しキャッシュに格納する処理を行っている。
またPromise.allを使用することで非同期に一度に行うように処理を行っている。
距離についても同様に以下のようにキャッシュを効かせることができる。
// 距離のキャッシュ
const distanceCache = new Map<string, number>();
// 座標をソートして一意のキーを生成
const sortedPoints = [point1, point2].sort((a, b) => a[0] - b[0] || a[1] - b[1]);
const key = `${sortedPoints[0].map((coord) => coord.toFixed(7)).join(',')}-${sortedPoints[1].map((coord) => coord.toFixed(7)).join(',')}`;
if (distanceCache.has(key)) {
return distanceCache.get(key) || 0;
}
// 水平距離
const horizontalDistance = distance(point1, point2, { units: 'kilometers' }) * 1000;
// 垂直距離
const heightDifference = Math.abs(elevation1 - elevation2);
// 斜距離
const slopeDistance = Math.sqrt(
horizontalDistance * horizontalDistance + heightDifference * heightDifference
);
// キャッシュに保存
distanceCache.set(key, slopeDistance);
5. ヘロンの公式で面積計算
あとは各三角形の3辺の長さから面積を求めるだけである。
参考までに以下のコードを使用する。
const s = (slopeDistance01 + slopeDistance02 + slopeDistance12) / 2;
const triangleArea = Math.sqrt(
s * (s - slopeDistance01) * (s - slopeDistance02) * (s - slopeDistance12)
);
あとは算出された各三角形の面積を合算するだけである。
まとめ
この処理を行うことでフロントのみで表面積を算出することができる。
ただし、ほとんどの三角形は単位面積の直角三角形が傾いただけなので、より効率的な算出方法があるだろう。