数学の軌跡を求める問題
問題
高校数学の数学IIの図形と方程式の問題です。
実数のパラメータ$t$によって,次のように定まる$x$,$y$を座標とする点Pの軌跡を求めます。
$$x=\frac{t}{1+t^2}\cdots\text{①},\quad y=\frac{1}{1+t^2}\cdots\text{②}$$
解答その1
$t$を消去して,$x$,$y$の関係式を作ります。
$x=ty$、$y\neq 0$なので,$t=\frac xy$として,②に代入し,
$$y=\frac{1}{1+\frac{x^2}{y^2}}=\frac{y^2}{x^2+y^2}$$
$$\therefore y(x^2+y^2)=y^2$$
$$\therefore y(x^2+y^2-y)=0$$
となります。$y\neq 0$より,
$$x^2+y^2-y=0$$
$$\therefore x^2+\left(y-\frac12\right)^2=\frac14$$
よって、点Pは
$$\text{中心}\displaystyle{\left(0,,\frac12\right)}\text{,半径}\displaystyle{\frac12}\text{の円周上}$$
にあることがわかります。
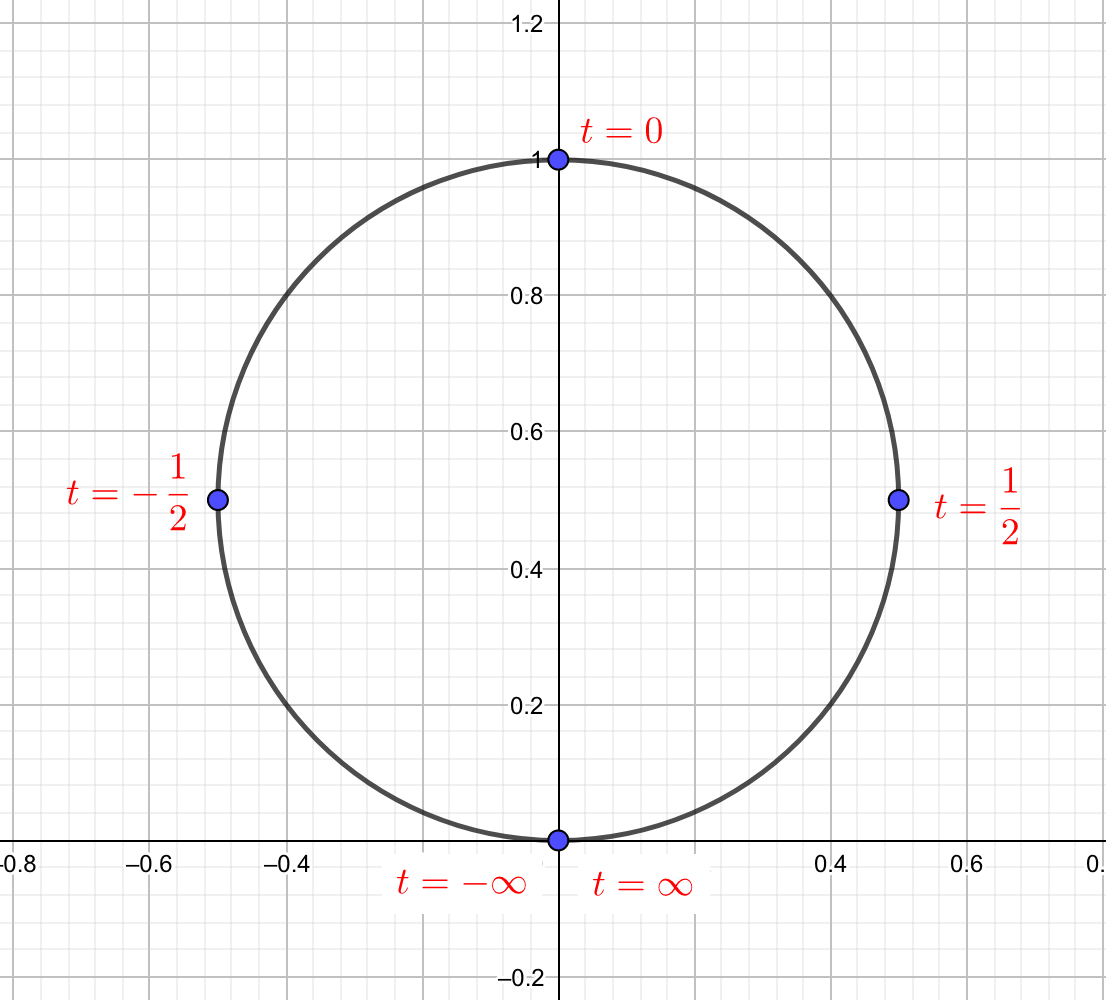
しかしながら,この円周上のすべての点に点Pが来るかどうかはわかりません。実際に,Pは原点に来ることはありません。
パラメータ$t$で点Pを追跡すると,下の図のようになります。