3x3の○×ゲーム（三目並べ）の全事象

はじめに

peing のサイトに『3×3の○×ゲームの全事象は何通りあるのでしょうか』と質問がきました。面白そうなので，考えてみることにしました。

ざっくりと

先手を○，後手を×とする。9個のマス

1 2 3
4 5 6
7 8 9

に○×○×○×○×○を順に入れていくこと考えます。

そうすると，
$$9!=362880\text{（通り）}$$
となります。

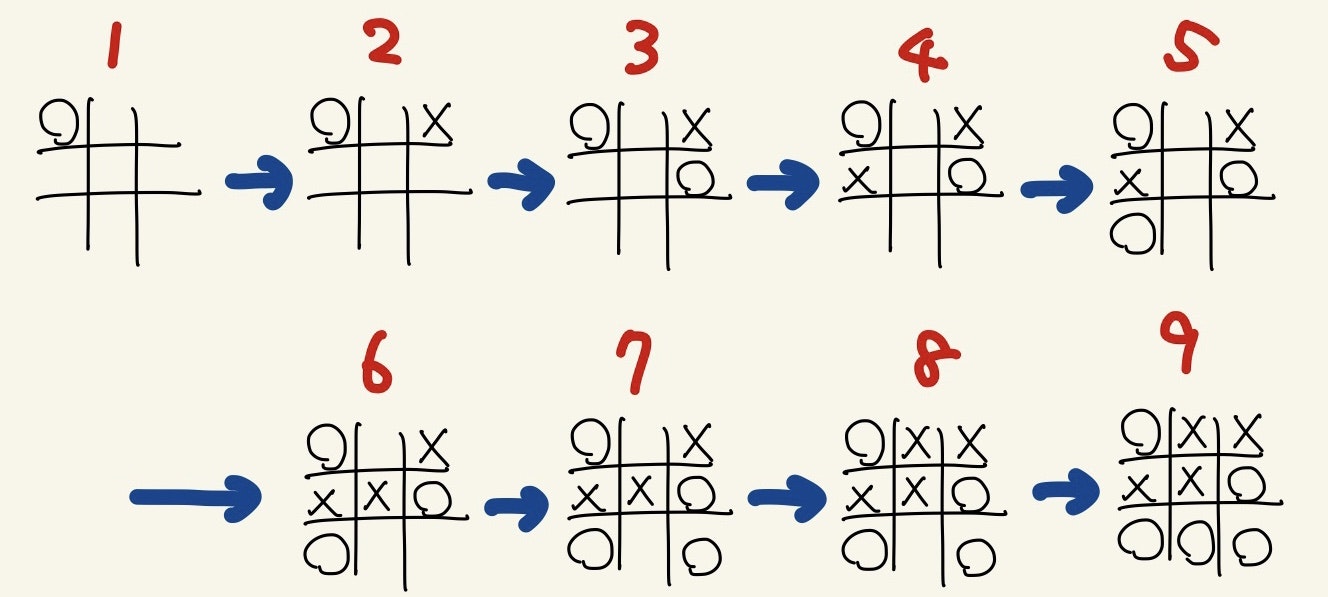
例 1

1	3	6	4	7	5	9	2	8
○	×	○	×	○	×	○	×	○

のケースは

で9回目で先手の勝利となります。

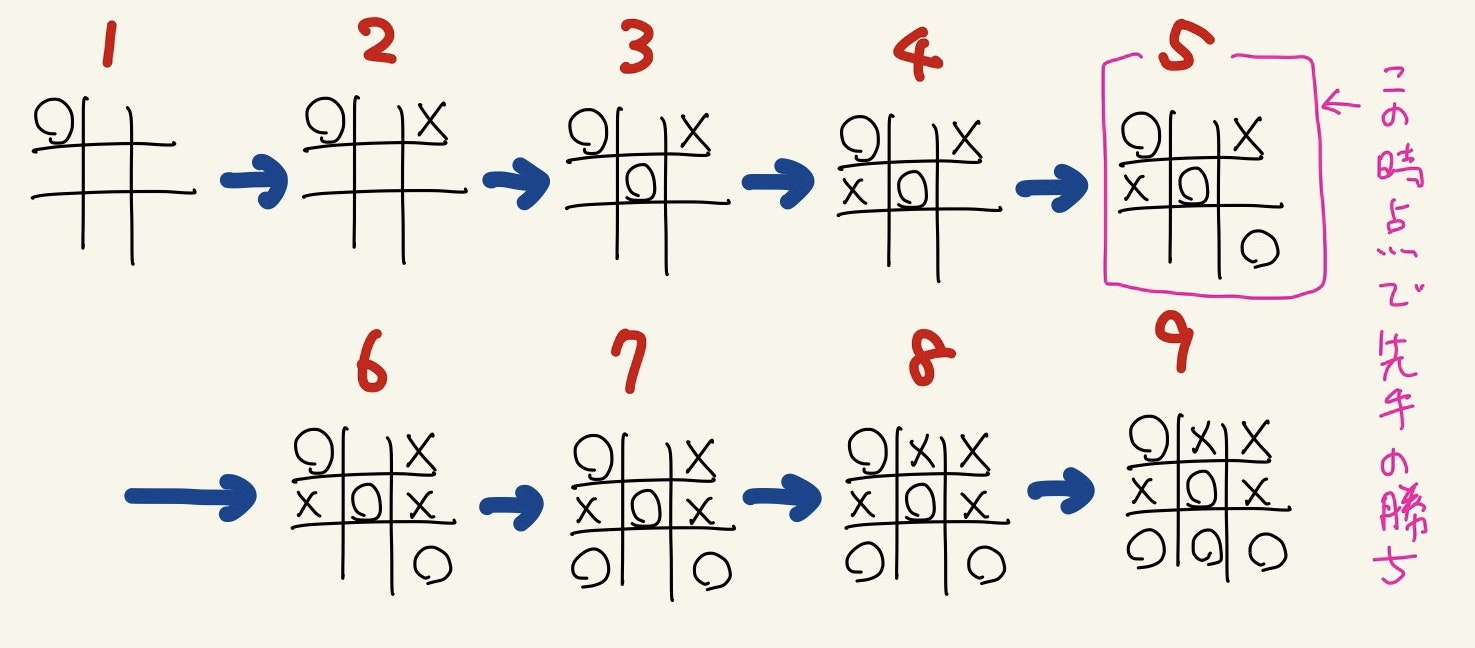
例 2

1	3	5	4	9	6	7	2	8
○	×	○	×	○	×	○	×	○

のケースは

で5回目で先手の勝利となります。通常は6手目から9手目はやりません。
6手目から9手目を変更しても，5回目で先手の勝利であることは変わらないので，
5回目までのところで，終了すると，例1のケースよりも$4!=24$倍の重みがあることになります。

本格的に数える！

まず，それぞれゲームの終わる回数別に分けていきます。

• 先手が勝つ場合
  ５手目，７手目，９手目

• 後手が勝つ場合
  ６手目，８手目

• 引き分けの場合
  ９手目

です。この６パターンで場合の数を計算します。

コーディング

3x3game.jl

function eva(X)
    a,b,c,d,e,f,g,h,i=X[1],X[2],X[3],X[4],X[5],X[6],X[7],X[8],X[9]
    abs(a+b+c)==3 || abs(d+e+f)==3 || abs(g+h+i)==3 || abs(a+d+g)==3 || abs(b+e+h)==3 || abs(c+f+i)==3 || abs(a+e+i)==3 || abs(c+e+g)==3
end

using Combinatorics
X=[1,2,3,4,5,6,7,8,9]
Y=collect(permutations(X))
Z=[]
for i=1:length(Y)
    A=Y[i]
    B=[0,0,0,0,0,0,0,0,0]
    for k in [1,3]
        B[A[k]]=1
        B[A[k+1]]=-1   
    end

    B[A[5]]=1
    if eva(B)
        append!(Z,5)
        continue
    end
    

    B[A[6]]=-1
    if eva(B)
        append!(Z,6)
        continue
    end 


    B[A[7]]=1
    if eva(B)
        append!(Z,7)
        continue
    end  


    B[A[8]]=-1
    if eva(B)
        append!(Z,8)
        continue
    end 
    
    
    B[A[9]]=1
    if eva(B)
        append!(Z,9)
        else append!(Z,10)
    end 
end

println("5手目で先手が勝つのは",Int(count(Z.==5)/24),"通り")
println("6手目で後手が勝つのは",Int(count(Z.==6)/6),"通り")
println("7手目で先手が勝つのは",Int(count(Z.==7)/2),"通り")
println("8手目で後手が勝つのは",count(Z.==8),"通り")
println("9手目で先手が勝つのは",count(Z.==9),"通り")
println("9手目で引き分けとなるのは",count(Z.==10),"通り")
println("先手の勝つ確率は",(count(Z.==5)+count(Z.==7)+count(Z.==9))/factorial(9))
println("後手の勝つ確率は",(count(Z.==6)+count(Z.==8))/factorial(9))
println("引き分けの確率は",(count(Z.==10))/factorial(9))

結果

5手目で先手が勝つのは1440通り
6手目で後手が勝つのは5328通り
7手目で先手が勝つのは47952通り
8手目で後手が勝つのは72576通り
9手目で先手が勝つのは81792通り
9手目で引き分けとなるのは46080通り
先手の勝つ確率は0.584920634920635
後手の勝つ確率は0.28809523809523807
引き分けの確率は0.12698412698412698

全事象の個数は
$$1440+5328+47952+72576+81792+46080=255168\text{（通り）}$$
です。

重みが違うので確率を求めるときは注意です。重みを考えると，
$$1440\times24+5328\times6+47952\times2+72576+81792+46080=362880=9!\text{（通り）}$$
となります。
先手の勝つ確率は
$$\frac{1440\times 24+47952\times2+81792}{362880}=0.584920634920635$$

後手の勝つ確率は
$$\frac{5328\times 6+72576}{362880}=0.28809523809523807$$

引き分けの確率は

$$\frac{46080}{362880}=0.12698412698412698$$

戦略的に進めると

確率は求まりましたが，実際にはゲームは先手・後手が必ず負けないように戦略的に配置することができるので，うまくやると，ずっと引き分けが続きます。

○と×を書く場所を戻さない形のくじ引きで決めていくと，それぞれの確率は前述のようになります。

＜参考＞
https://ja.wikipedia.org/wiki/三目並べ