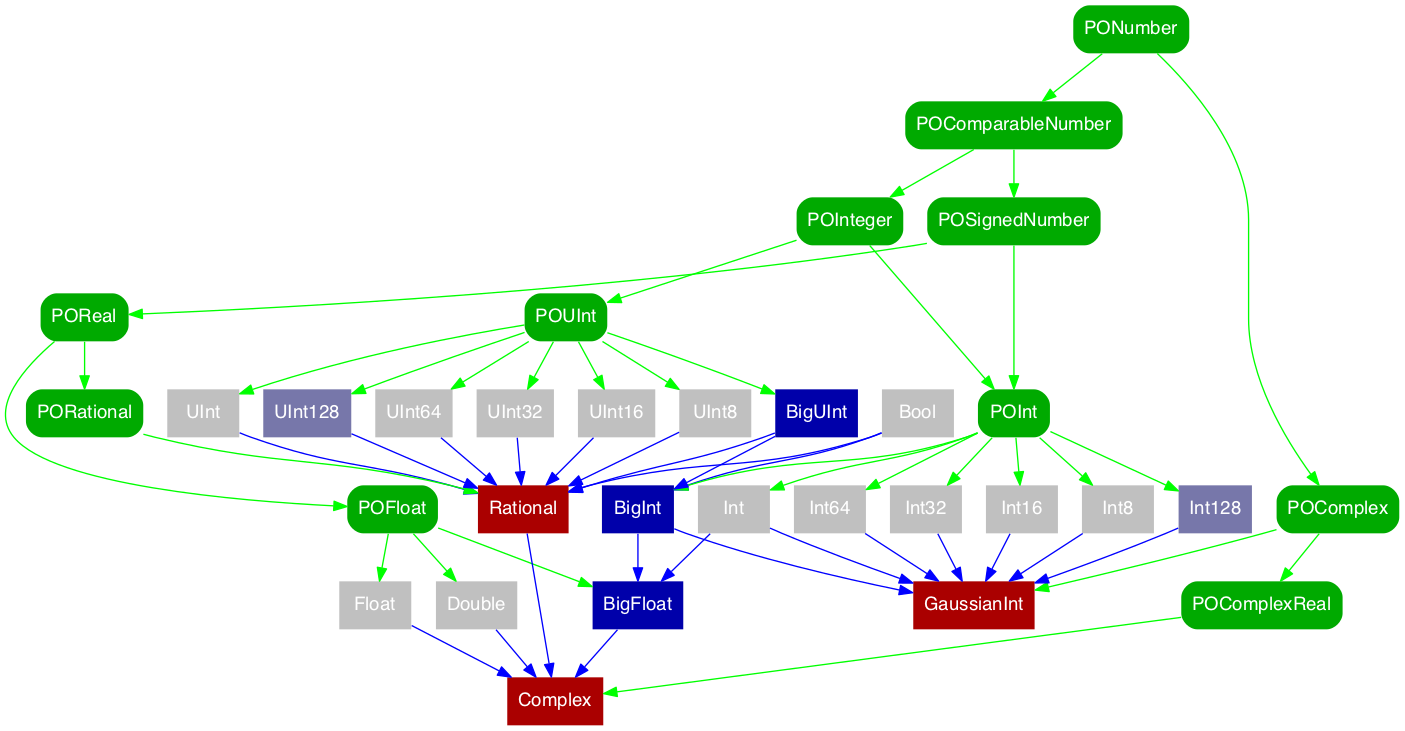
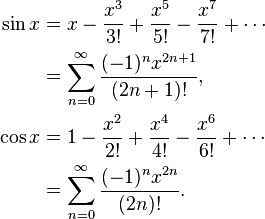まだ荒削りですが、お披露目してもいいところまで来たので。
売り口上
これでSwiftでも
- GMPとか外部ライブラリなしで任意精度整数(BigInt)や任意精度分数(BigRat)や任意精度浮動小数点数(BigFloat)が使えるようになります。
- 外部依存がないので、Xcodeでなくてもswiftcがあれば使えます。もちろんOS XだけでなくてLinuxもサポート
- その任意精度数も、四則演算以外の演算を最初からサポートしています。整数は素数判定できますし、任意精度実数は
<math.h>の関数を使えます。
これだけでもかなりハッピーになれます。
でも本当のウリは、そこじゃないんですよ…
承前: 古き良きCの時代
例えばman powとしてみます。こんな答えが返ってくるでしょう。
SYNOPSIS
#include <math.h>
double
pow(double x, double y);
long double
powl(long double x, long double y);
float
powf(float x, float y);
なんで全く同じことをする関数が三つあるのか?
異なった型ごとに、違う実装が必要だから。
20世紀までは仕方ないことだったのかもしれませんが、21世紀ももう1/8過ぎた2016年にこんなの付き合ってられませんよね?
で、Swiftでは、
同じpowという名前でDoubleにもFloatにも対応しています。やったね!
import Cocoa // this is an OSX playground
let twelveTet = pow(2.0, 1.0/12)
pow(Float(twelveTet), 12) // not exactly 2.0 but you get the point
でも、使う側でなくて作る側として、どうしたらそのような関数が書けるでしょう?
とりあえずfibってみる
とりあえずみんな大好きフィボナッチ数でも数えてみますか。前世紀脳だと、こんな感じになりますか。
勤勉なやり方
func fib(n:Int8)->Int8 { return n < 2 ? i : fib(n-2)+fib(n-1) }
func fib(n:Int16)->Int16 { return n < 2 ? i : fib(n-2)+fib(n-1) }
func fib(n:Int32)->Int32 { return n < 2 ? i : fib(n-2)+fib(n-1) }
func fib(n:Int64)->Int64 { return n < 2 ? i : fib(n-2)+fib(n-1) }
// hey, don't forget UInt(8|16|32|64)?
つまり、型シグネチャーが異なる同名の関数を、型の数だけ繰り返す、と。
やってられるか!
<T:Hoge>でどうHogeる?
幸いSwiftには総称型があります。ならこう書ける?
func fib<T>(i:T)->T { return i < 2 ? i : fib(n-2)+fib(n-1) }
残念でした。Tで<できたり、Tどうし+できたりって誰が保証してくれるんですか?
それを保証してくれるのが、Protocolなんですが…
func fib<T:Hoge>(i:T)->T { return i < 2 ? i : fib(n-2)+fib(n-1) }
で、Hogeプロトコルが<と+をサポートしてさえすれば、これは動くはずです。
が、そのHogeってどこにあるの?
import PONS
PONSの役割は、それを提供すること。
import PONS // make sure you have built the framework before this!
func fib<T:POInteger>(n:T)->T { // with a little better algorithm
if n < T(2) { return n }
var (a, b) = (T(0), T(1))
for _ in 2...n {
(a, b) = (b, a+b)
}
return b
}
ちょっとアルゴリズムを改良しました。
で、これが本当に動くのか?
let F11 = fib(11 as Int8)
let F13 = fib(13 as UInt8)
let F23 = fib(23 as Int16)
let F24 = fib(24 as UInt16)
let F46 = fib(46 as Int32)
let F47 = fib(47 as UInt32)
let F92 = fib(92 as Int64)
let F93 = fib(93 as UInt64)
動くんです。
しかし、PONSの本領はここからがはじまりです。あなたが苦労して実装した新たな整数方も受け付けてGeneric Programmingを名乗れるというものです。
でもどうやってそれを証明する?
そのためにBigInt実装しちゃいましたよ。てへぺろ。
よってこれが動きます。
let F666 = fib(666 as BigInt)
ちなみに6859356963880484413875401302176431788073214234535725264860437720157972142108894511264898366145528622543082646626140527097739556699078708088だそうです。
整数だけで許されるのは小学生までだよねー
カントールをパワハラして後世の評判を多いに下げたクロネッカーは、こうのたまいました。
整数は神の作ったものだが、他は人間の作ったものである
人間上等、というわけで我々はさまざまな数を作ってきました。有理数に実数にそして複素数。あの古き良きCですらC99で複素数をサポートしたぐらいです。それくらい数値というのは切実なわけです。
ところがSwiftは標準で複素数をサポートしていません。というわけで書いたのが
なのですが、これを書いたことでむしろ欲求不満は高まりました。
「たしかに総称型で、たしかにIntもDoubleも受け入れられるけど、BigIntとかRationalとか突っ込んでも大丈夫?っつうかそれ以前に突っ込むべき数値型が見当たらないんだが」
というわけで実装しましたよ。Genericで「整数」型ならBigIntだって分子と分母に使えるRationalに…
let bq = BigInt(1).over(bn) // (1/18446744073709551617)
bq + bq // (2/18446744073709551617)
bq - bq // (0/1)
bq * bq // (1/340282366920938463500268095579187314689)
bq / bq // (1/1)
bq.denominator == bn // true, of course!
bq.reciprocal.numerator == bn // so is this
そのRational含め、「実数」型なら実部と虚部に使えるComplex。
let bz = bq + bq.i // ((1/18446744073709551617)+(1/18446744073709551617).i)
bz + bz // ((2/18446744073709551617)+(2/18446744073709551617).i)
bz - bz // ((0/1)+(0/1).i)
bz * bz // ((0/1)+(2/340282366920938463500268095579187314689).i)
bz / bz // ((1/1)+(0/1).i)
動くぞ、動くぞ!
でも、整数におけるfact(orial)やfib(onacci)なようなデモを、実数とか複素数でやるにはどうしたらいいの?
<math.h>な関数が、総称型でも動くことを見せつければいい!
という気持ちでやった。後悔はしていない。
Double.sqrt(2)
Double.sqrt(2) // 1.414213562373095
BigRat.sqrt(2) // (112045541949572279837463876455/79228162514264337593543950336)
BigFloat.sqrt(2) // 1.414213562373095048801688724198
Complex.sqrt(-2) // (0.0+1.4142135623731.i)
Complex.sqrt(BigRat(-2)) // 112045541949572279837463876455/79228162514264337593543950336).i)
個人的に一番感動したのは、これ。
Complex.exp(Double.PI.i) // (-1.0+1.22464679914735e-16.i) != (-1.0+0.0.i) // :(
// default 64-bit precision is still not good enough…
Complex.exp(BigRat.pi().i) // (-(1/1)-(1/4722366482869645213696).i)
// but with 128-bit precision…
Complex.exp(BigRat.pi(128).i) // (-(1/1)+(0/1).i) // as it should be!
128bit精度の有理数型なら e ** πi == -1 に本当になるんです!(厳密にはsin(pi) < ulpのというわけなのですが)。
すべての型別実装を、生まれる前に消し去りたい
PONSの存在意義は、 Write once, runs on every type (that conform to the protocol) が、数値型でも成立することを示すことにあります。
例えば三角関数のcosとsinは、(現時点において)
以下のように定義されています。
public static func cos(x:Self, precision:Int = 64)->Self {
if let dx = x as? Double { return Self(Double.cos(dx)) }
let px = Swift.max(x.precision, precision)
let epsilon = Self(Double.ldexp(1.0, -px))
let x2 = x * x
var (r, t) = (Self(1), Self(1))
for i in 1...px {
t *= x2.divide(Self((2 * i - 1) * 2 * i), precision:px)
t.truncate(px + 32)
r += i & 1 == 1 ? -t : t
r.truncate(px + 32)
if t < epsilon { break }
}
return r.truncate(px)
}
public static func sin(x:Self, precision:Int = 64)->Self {
if let dx = x as? Double { return Self(Double.sin(dx)) }
let px = Swift.max(x.precision, precision)
let epsilon = Self(Double.ldexp(1.0, -px))
let x2 = x * x
var r = x < 0 ? -x : x
var t = r
for i in 1...px {
t *= x2.divide(Self((2 * i + 1) * 2 * i), precision:px)
t.truncate(px + 32)
r += i & 1 == 1 ? -t : t
r.truncate(px + 32)
if t < epsilon { break }
}
return x < 0 ? -r.truncate(px) : r.truncate(px)
}
数学者でなくとも、これはテイラー展開
をほぼそのままであることが見て取れるかと思いますが、重要なのはこれがFloatやDoubleはおろか、BigRat = Rational<BigInt>でもBigFloatでもまったく変更なしに動くこと。一行目に
if let dx = x as? Double { return Self(Double.sin(dx)) }
とはありますが、これはコメントアウトしても動きます(その分Double.cosやDouble.sinは遅くはなりますが)。
なんで/でなくて.divideなのか、.truncateは何をしているかとかは後日別記事で紹介する予定ですが、いずれにせよ将来Float128とか実装したとしても、サインコサインできちゃうわけです。
とりあえず使ってみるには
git clone して PONS.xcworkspace開いて、フレームワークをbuildしたらplaygroundで遊べます。Xcodeがなくともmake replすればコマンドラインから遊べます。自分のプロジェクトで使いたい場合は、ソースをまるっとコピーするだけです。
当初予定を超えて大きなプロジェクトになったので、まだまだ全然説明したりないのですが、とりあえず「なんぞこれ」はこれで伝わっているといいなあ…
Enjoy!
Dan the Protocol-Oriented Swift Programmer