はじめに
Tableauでレーダーチャートを作ったり、線グラフを曲げたり(円を描いたり)する方法として、データから三角関数を使って座標を計算し、その座標を行・列にプロットしていく方法があります。
たとえばこんなの(URL)

レーダーチャートや、上記のような曲がった棒グラフ(ラジアルバーチャート)の作り方を解説しているブログはあるものの、座標プロットの基本を紹介しているものが見当たらなかったので、ちょっと書いてみようと思います。
Tableau2024.2でViz Extensionが導入され、高度なチャートが簡単に作れるようになりましたが、そんな今だからこそ、動作原理を学んでみましょう。
注意
本記事は、三角関数を使った座標プロットの方法のみ紹介します。この手法を用いた各チャートの作成方法までは解説しません。
三角関数の定義
まず第一に、本記事で使用する「三角関数(sin,cos)」について一応定義をしておきましょう。
「一般角θに対する、sinθ, cosθの定義を述べよ。」という問題が1999年にどこかの大学入試問題で出た、というのは一部界隈で有名な話ですね。
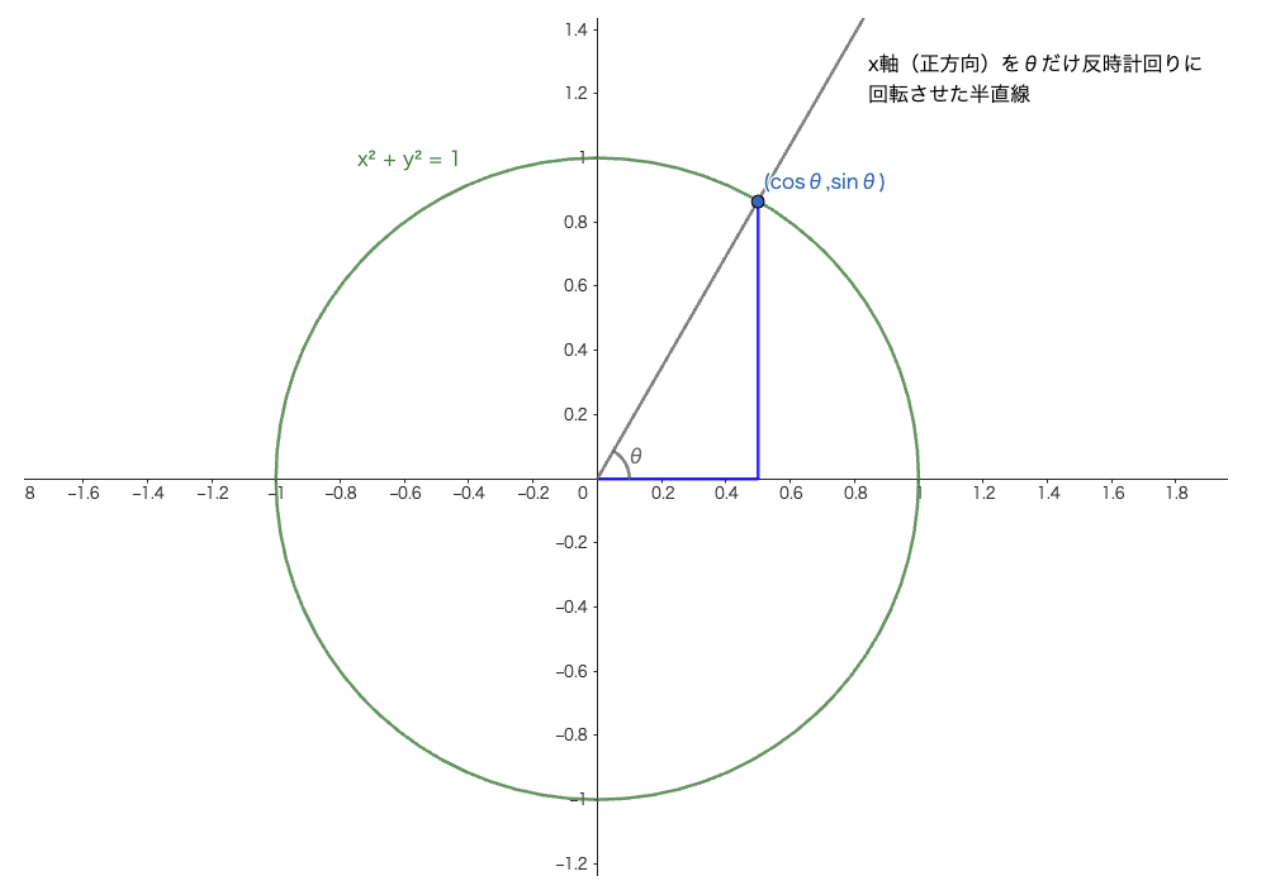
直角三角形の角(90°未満)ではなく、一般角(任意の実数)に対する定義なので、「円: $x^2 + y^2 = 1$ (単位円と呼ぶ)と、x軸の正の部分を原点を中心にθだけ反時計回りに回転させた半直線との交点のx座標をcosθ、y座標をsinθと定義」します。
言葉ではわかりづらいですが、定義を図にすると以下のようになります。
とりあえずプロットしてみる
いったん角度情報だけのデータを使って、Tableau上に座標をプロットしてみましょう。
データセットはとても簡単な以下のようなものを用意します。
Angle
0
30
60
90
120
150
180
210
240
270
※続く説明のため、360°までではなく270°までにしています
まず、角度に対するsin、cosを求めましょう。TableauにはSIN()関数,COS()関数が用意されていますのでこれらを使うのですが、 関数の引数となる角度は弧度法で記載しなければならない ことに気をつけてください。
・度数法:いわゆる0°〜360°で角度を記述したもの
・弧度法:360°=2π として角度を記述したもの
※数学の記事ではないので厳密な定義ではありません
今回のデータセットは、度数法で0°と270°を記載していますから、弧度法への変換が必要です。もちろん、Tableauには弧度法への変換関数があるので安心してください。
RADIANS()関数を使って、度数法の角度を弧度法の角度に変換します。
一度にsin、cosまで求めるとすると、計算式は以下のようになります。
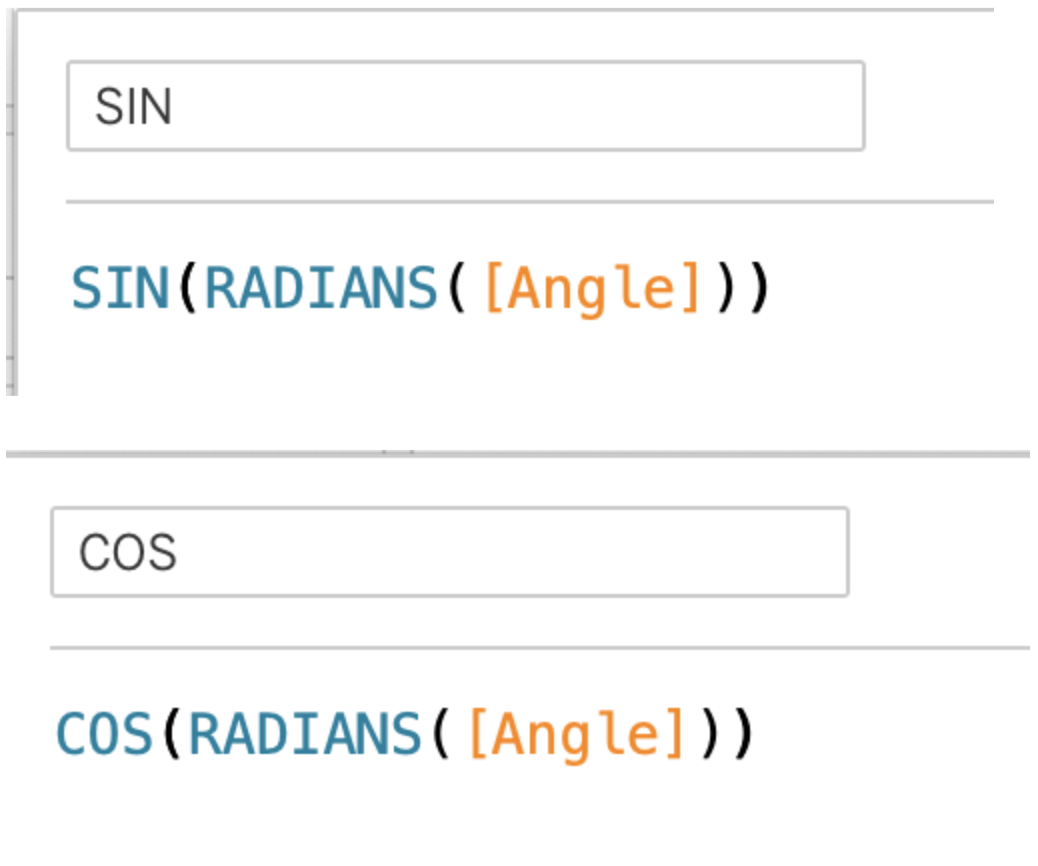
準備は整ったので、早速プロットしてみましょう。
Angleがメジャーとして読み込まれている場合はディメンションに変換したうえで、
・Angleを詳細とテキスト
・COS(最小値)を列
・SIN(最小値)を行
に設定します。
※今回、同じAngleは1行しかありませんから、メジャーは合計でもよいのですが、実データを使用する時に「あれ?」とならないように念の為最小値を使用しています。Angleが同じであれば、計算されるSIN,COSの値も同じになるので、もちろん最大値でも平均でもOKです。
そうすると以下のように点が座標平面上にプロットされます。
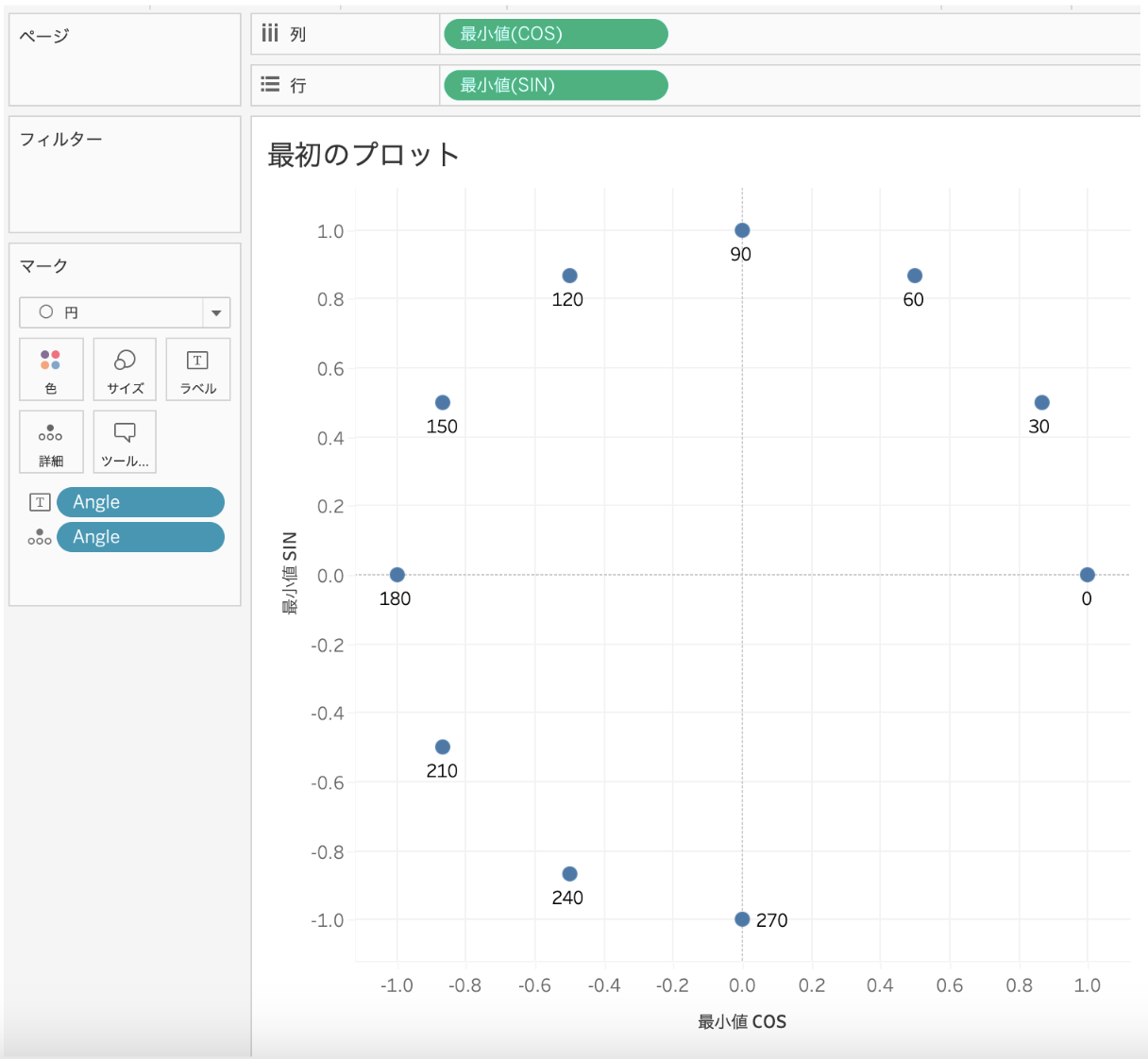
ここで留意してほしいのは、 それぞれの点が、座標(1,0) = (cos0°, sin0°)を出発点として、反時計回りに並んでいることです。これは冒頭の三角関数の定義に照らすと明らかですね。
しかし、Tableauの優れたビジュアライゼーションは、時計回りに座標がプロットされていたり、円弧が描かれていたりすることがよくあります。というか、そっちのパターンのほうが多いですよね。
時計回りにするにはどうすればよいでしょうか?
答えは簡単で、「X座標とY座標を入れ替えて、SINをX座標、COSをY座標にすればOK」 です。
先ほどのシートを複製して、行と列を入れ替えると下のようになります。
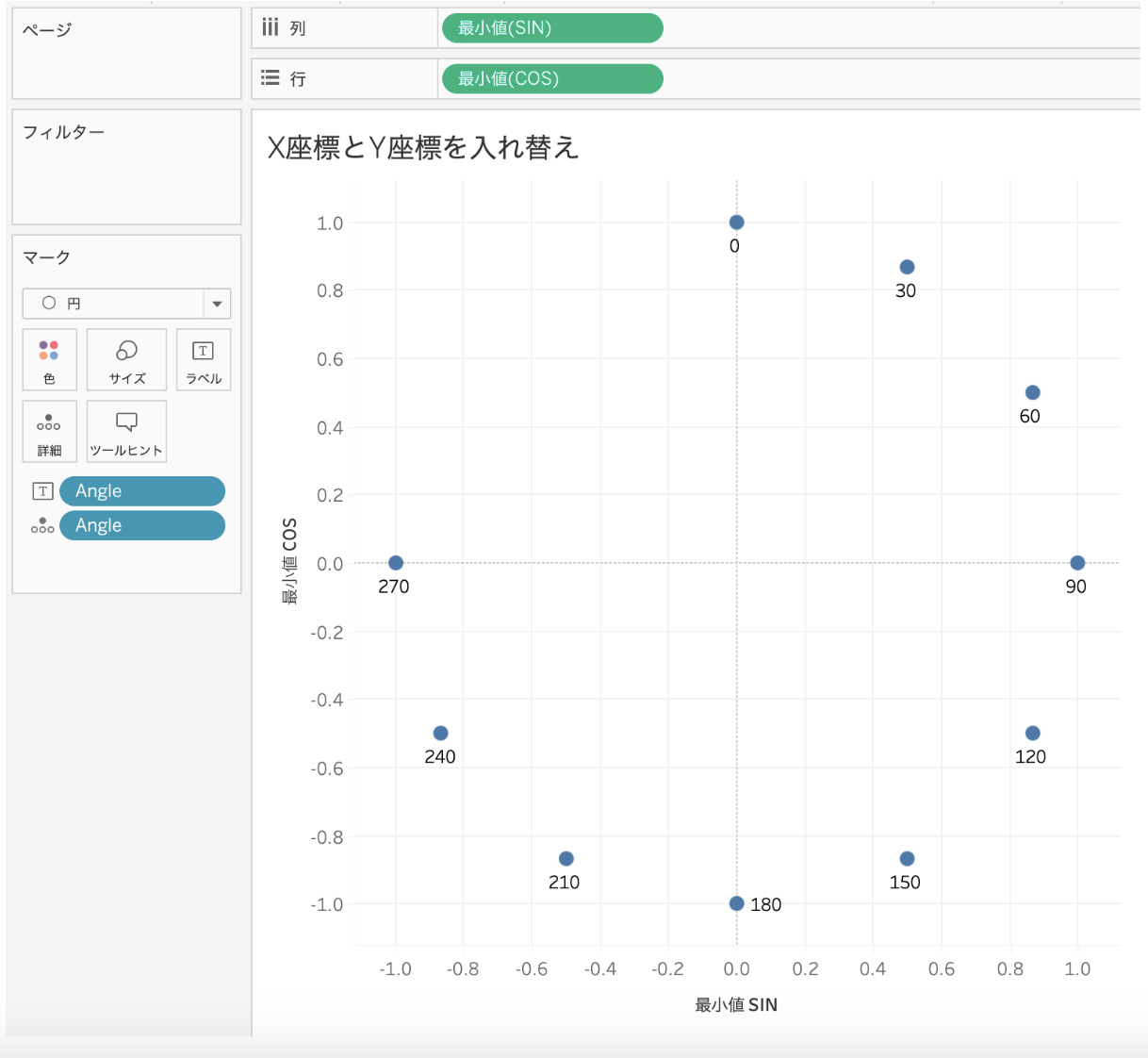
点(0,1) = ( sin0°, cos0° ) を出発点として、時計回りに点を並べることができました。
サンプルでは座標の数が少ないので円弧のようにはなりませんが、マークタイプを「線」に、「Angle」を「パス」にすると、線でつなぐことができます。なんとなくラジアルバーチャートに近くなってきましたね。
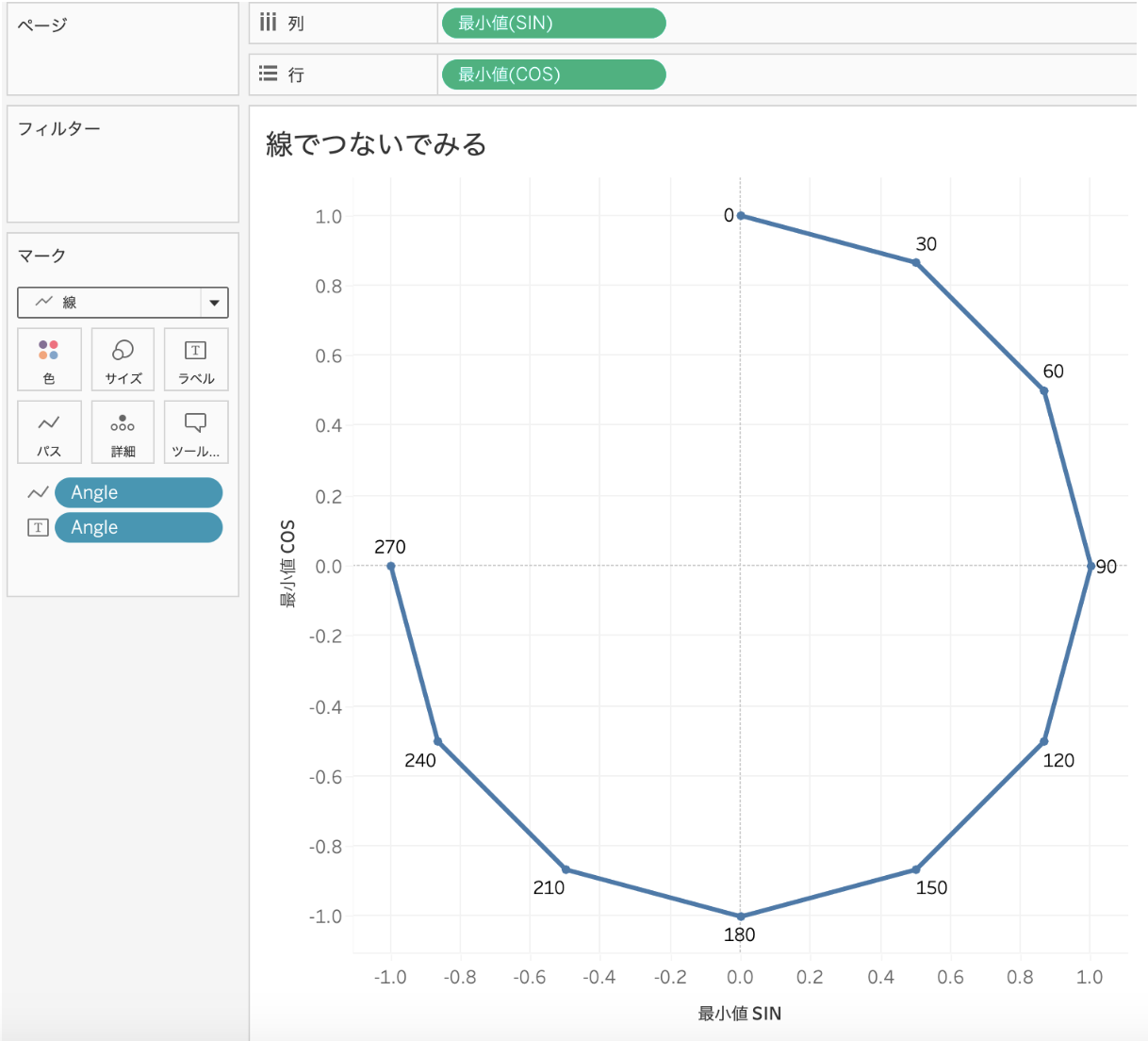
三角関数を使って座標をプロットするとき、
・反時計回りにプロットするときはCOSをX座標にする
・時計回りにプロットするときはSINをX座標にする
と覚えておけば大丈夫です。
実際のデータで少しやってみる
本記事は基本的な考え方のみお伝えするものです!といっても、何も作らないのも…ということで、スーパーストアのデータを使って、いくつかの計算式を作るだけでできるチャートを作ってみます。
完成系は以下の通りです。

1月〜12月の売上が、時計回りに並んで、線でつながれています。
売上の大きさは、原点からの距離で表されています。
準備
データを2021年にフィルタします(本記事ではTableauDesktop2024.1に付属のデータを使っています)
次に、1ヶ月あたりの角度を何度にすればよいかを考えます。
1年は12ヶ月ですから、360°÷12=30°が一ヶ月あたりの角度になることがわかります。
30という数値を入れておいてもいいのですが、いったん計算式を設定しておくこととします。

度数法ではなく、弧度法で最初から角度を計算するときは、PI()関数を使います。

次に、月に順番を振るためにIndex()関数を使用します。
このあとの数式に直接書いてもいいのですが、いったん計算フィールドとして用意しておきます。
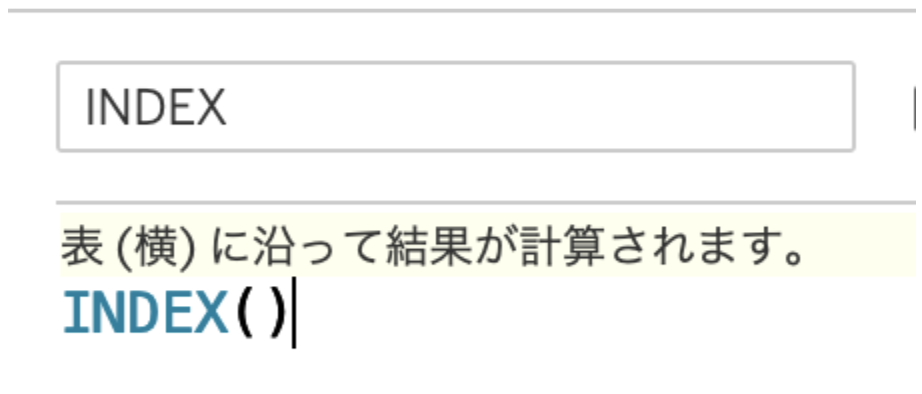
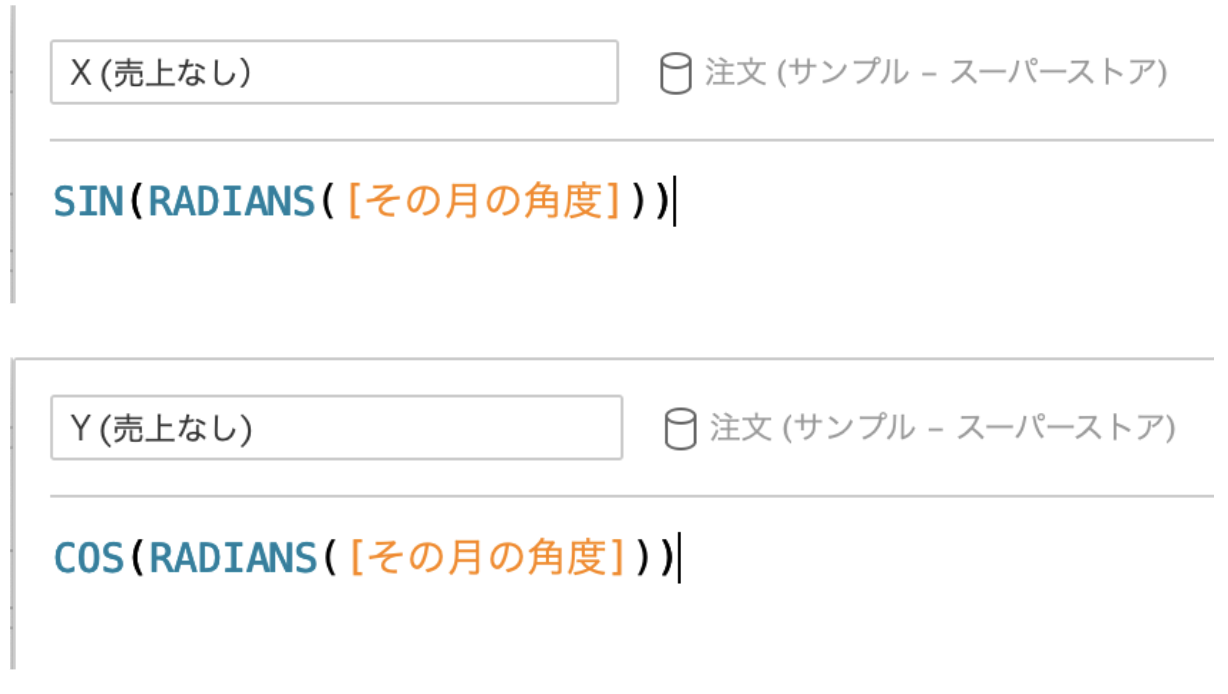
いったん、売上の大きさを無視して、とりあえず月をシートにプロットしてみます。
以下の前提で進めます。
・スタートは真上とし時計回りに月を並べる(つまりX座標がSIN、Y座標がCOS)
・1月をスタートとする
X,Y座標をそれぞれ作るのですが、ここでINDEXを使用します。
INDEXは(後に行う設定によって)1月=1, 2月=2,,, という風に振られていきます。
1月あたりの角度が30°ですので、この角度にINDEXを掛ければ各月の角度が求められそうです。
ただし、「1月をスタートとする」という前提にしていますので、1月は0°でなければなりません。Indexは1から始まっているので、1を引いて0始まりにしてあげればよさそうです。
よって、各月の角度を求める計算式は以下のようになります。

さて、角度が求まったので、X座標、Y座標を計算しましょう。今回は時計回りですから、以下の計算式で座標が求められますね。
※「1月あたりの角度」を弧度法で求めた場合はRADIANS関数は不要です
チャートの作成
さて、計算フィールドが揃ったのでプロットしていきます。
・オーダー日の月を詳細とテキストに
・Xを列に → 「次を使用して計算」で「オーダー日」を選択
・Yを行に → 「次を使用して計算」で「オーダー日」を選択
とすると、以下のようになり、正しくプロットできたことがわかります。
※表計算の方向を「オーダー日」にすることで、1月〜12月に順番に番号(INDEX)が振られます
角度の計算は良さそうなので、売上の大小を反映しましょう。売上は原点からの距離で表すことにしていますので、X座標、Y座標それぞれに売上の合計を掛けてあげます。
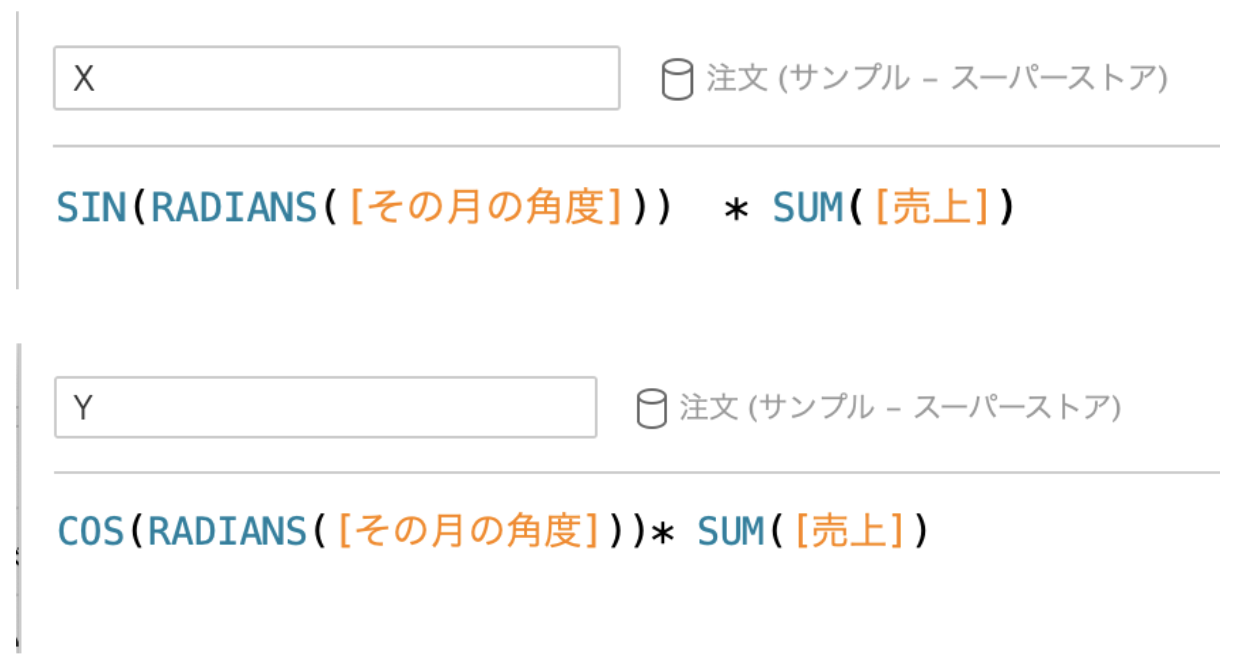
そして、以下の操作をすると背景となる図形が出来上がります。
・マークタイプを「多角形」に
※これをしないと現在のデータでは、12月と1月がつながりません
・オーダー日の月を「パス」に
・色の「不透明度」「枠線」を調整
・X軸、Y軸の範囲を正方形になるように調整(今回は-5M〜5Mの範囲にしています)

これだけだと各月の位置がわかりにくいので、「円」マークもおいて二重軸にします。
・列シェルフのXを複製
※行シェルフのYを複製してもよいが本記事ではXを複製したものとして説明します
・複製したほうのマークタイプを「円」に変更
・色の不透明度、サイズを調整
・オーダー日の月を「ラベル」に
・二重軸にする
・(オプション)売上(合計)をツールヒントに
これで、完成系が出来上がりました。

このような表現方法に意味があるか、、、はさておき、
・ディメンションの数から1つあたりの角度を計算
・Index()関数を使って番号を振る
・1つあたりの角度とIndexを使って各マークの角度を計算
・SIN,COSを計算して座標にプロット
という流れを掴んでいただけたのではないかと思います。
おまけ 開始位置を変更する
SINをX座標にしたとき、開始位置は上(0,1)になるという説明をしましたが、他の位置から始めたいときはどうしたらよいでしょうか?
たとえば、ゲージチャートは、左(−1,0)の地点から、右(1,0)に向かって時計回りにチャートが伸びていきますよね。

出典: WorkoutWednesday 2024 Week 14
開始位置を変えたいときは、「角度を足し引きしてずらす」ことで対処します。
例えば上のゲージチャートの例であれば、通常は0°(上)から始まるところ、左に90°だけ回転させれば-90°(=270°、左)から始めることができます。
いま、(三角関数の定義とは違って)時計回りに角度が増えていく前提にしているので、左(反時計回り)に回転させたいときは、回転させたい分だけ角度を引いてあげればOKです。
最初のシンプルなデータを使ってやってみましょう。
COS、SINの式をそれぞれ以下のように変更します。

弧度法に直す前に度数法で90°引くので、引き算の位置に注意してください。
もしRADIANS()の関数の外で引くなら、90°はπ/2なので、こうなりますね。
SINまたはCOS (RADIANS( [Angle] ) - PI()/2 )
このように計算式を変更した上で、Angleを180までにフィルタしてあげると、以下のように左から右に円弧状に点が並びます。

おわりに
本記事では三角関数を用いた座標プロットの基本を紹介しました。冒頭に記載した通り、このテクニックを用いたさまざまなチャートの作り方は紹介していませんが、他の方のブログなどを参照される際に、本記事の内容を念頭に置いておくと理解がより容易になると思います。