matplotlib ３次元グラフ（アスペクト比調整と多角形塗りつぶし）

はじめに

格子桁解析を行っているのだが、結果の断面力図は３次元で表示する必要がある。これまで3次元描画はGMT（Generic Mapping Tools）を使っていたのだが、なんとかPythonでやってみたい。
Pythonで３次元描画を行う上での問題点は、「各軸の縮尺（アスペクト比）を合わせること」および、「多角形（ポリゴン）の着色」であったが、一応これらを思ったとおりに実行できるようになったので、基本的なところを紹介しておく。なお、この原稿の下書きは、最近使い出したメモアプリ（マークダウンエディタ） Obsidian で行っている。なかなかいいですぞ。

環境は以下の通り。

• macOS Monterey
• Python 3.9.7
• matplotlib 3.4.3

参考サイトを以下に示しておく。

アスペクト比関係
３Dポリゴン関係（１）
3Dポリゴン関係（２）

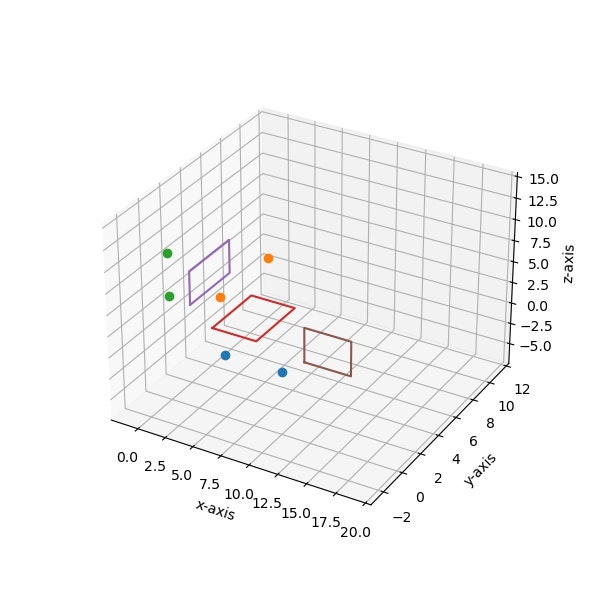
デフォルト描画

デフォルトだと背景やアスペクト比が自動で設定されてしまい、ゴタゴタすぎる感がある。

以下に作図プログラムを示す。

import matplotlib.pyplot as plt 

fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
xmin,xmax=-2,20
ymin,ymax=-3,12
zmin,zmax=-7,15
ax.set_xlim3d(xmin, xmax)
ax.set_ylim3d(ymin, ymax)
ax.set_zlim3d(zmin, zmax)
ax.set_xlabel('x-axis')
ax.set_ylabel('y-axis')
ax.set_zlabel('z-axis')
# plot bullets
ax.plot([5,10],[0,0],[0,0],'o')
ax.plot([0,0],[5,10],[0,0],'o')
ax.plot([0,0],[0,0],[5,10],'o')
# plot square shape
ax.plot([2,6,6,2,2],[2,2,6,6,2],[0,0,0,0,0],'-')
ax.plot([0,0,0,0,0],[2,6,6,2,2],[2,2,6,6,2],'-')
ax.plot([12,16,16,12,12],[0,0,0,0,0],[2,2,6,6,2],'-')

plt.savefig('fig_1.jpg',dpi=100)
plt.show()

アスペクト比をあわせる・視点を変える

ここでは、以下を実行。

• (1) 視点を変更する。
• (2) デフォルトの軸・背景はとってしまう。
• (3) x,y,z軸の縮尺を合わせる（アスペクト比を調整）。

(1) ax.view_init(elev=30, azim=-135)
(2) plt.axis('off')
(3) ax.set_box_aspect((xmax-xmin,ymax-ymin,zmax-zmin))

視点は、elev ：z軸を見下げる角度、azim ：x-y平面の回転角で指定する。

アスペクト比の調整はax.set_box_aspect((1,1,1)) とするようなものをよく目にするが、x,y,z軸の長さが等しいときにしか使えないため、ここではそれぞれの軸の長さを指定している。

以下に作図プログラムを示す。３つの正方形の座標を与えているが、一応正方形になっているようである。

import matplotlib.pyplot as plt 

xmin,xmax=-2,20
ymin,ymax=-3,12
zmin,zmax=-7,15

fsz=10
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=30, azim=-135)
plt.axis('off')
ax.set_box_aspect((xmax-xmin,ymax-ymin,zmax-zmin))
ax.set_xlim3d(xmin, xmax)
ax.set_ylim3d(ymin, ymax)
ax.set_zlim3d(zmin, zmax)
# draw axes
ax.plot([xmin,xmax],[0,0],[0,0],'-',color='#000000',lw=1)
ax.plot([0,0],[ymin,ymax],[0,0],'-',color='#000000',lw=1)
ax.plot([0,0],[0,0],[zmin,zmax],'-',color='#000000',lw=1)
ax.text(xmax,0,0,'x',fontsize=fsz)
ax.text(0,ymax,0,'y',fontsize=fsz)
ax.text(0,0,zmax,'z',fontsize=fsz)
# plot bullets
ax.plot([5,10],[0,0],[0,0],'o')
ax.plot([0,0],[5,10],[0,0],'o')
ax.plot([0,0],[0,0],[5,10],'o')
# plot square shape
ax.plot([2,6,6,2,2],[2,2,6,6,2],[0,0,0,0,0],'-')
ax.plot([0,0,0,0,0],[2,6,6,2,2],[2,2,6,6,2],'-')
ax.plot([12,16,16,12,12],[0,0,0,0,0],[2,2,6,6,2],'-')

plt.savefig('fig_2.jpg',dpi=100)
plt.show()

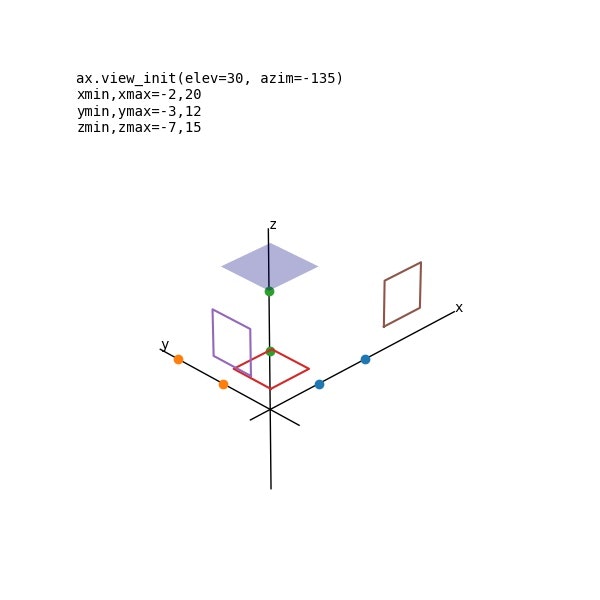
塗りつぶし四角形・文字を加える

多角形の塗りつぶしを行うには以下をインポート。

from mpl_toolkits.mplot3d.art3d import Poly3DCollection

プロット及び塗りつぶしは以下の要領で行う。

xx=np.array([0,5,5,0,0])
yy=np.array([0,0,5,5,0])
zz=np.array([10,10,10,10,10])
verts = [list(zip(xx,yy,zz))]
ax.add_collection3d(Poly3DCollection(verts,facecolor='#000080',alpha=0.3))

点の座標指定はリストでも問題ないが、描画軸の入れ替えを行う際などで符号を付ける際の扱いがnumpy配列のほうが便利なので、numpy配列にしている。verts を指定するリストは zip で囲うところがミソらしい。色および透明度の指定は、Poly3DCollection() の中で行うことができる。

文字列の描画は３次元座標でも指定できるが、ここでは、グラフ領域を(0,0)~(1,1) で表す座標を用いて、以下のように文字を描画している。すなわち、グラフ領域の左上に、上詰め・左詰めで文字列 ls を配置している。

ax.text2D(0, 1, ls, va='top',ha='left',transform=ax.transAxes,fontsize=fsz)

作図用プログラムを以下に示す。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np


xmin,xmax=-2,20
ymin,ymax=-3,12
zmin,zmax=-7,15

fsz=10
fig = plt.figure(figsize=(6,6))
plt.rcParams['font.family']='monospace'
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=30, azim=-135)
plt.axis('off')
ax.set_box_aspect((xmax-xmin,ymax-ymin,zmax-zmin))
#ax.set_box_aspect((1,1,1))
ax.set_xlim3d(xmin, xmax)
ax.set_ylim3d(ymin, ymax)
ax.set_zlim3d(zmin, zmax)
# draw axes
ax.plot([xmin,xmax],[0,0],[0,0],'-',color='#000000',lw=1)
ax.plot([0,0],[ymin,ymax],[0,0],'-',color='#000000',lw=1)
ax.plot([0,0],[0,0],[zmin,zmax],'-',color='#000000',lw=1)
ax.text(xmax,0,0,'x',fontsize=fsz)
ax.text(0,ymax,0,'y',fontsize=fsz)
ax.text(0,0,zmax,'z',fontsize=fsz)
# plot bullets
ax.plot([5,10],[0,0],[0,0],'o')
ax.plot([0,0],[5,10],[0,0],'o')
ax.plot([0,0],[0,0],[5,10],'o')
# plot square shape
ax.plot([2,6,6,2,2],[2,2,6,6,2],[0,0,0,0,0],'-')
ax.plot([0,0,0,0,0],[2,6,6,2,2],[2,2,6,6,2],'-')
ax.plot([12,16,16,12,12],[0,0,0,0,0],[2,2,6,6,2],'-')
# colored polygon
xx=np.array([0,5,5,0,0])
yy=np.array([0,0,5,5,0])
zz=np.array([10,10,10,10,10])
verts = [list(zip(xx,yy,zz))]
ax.add_collection3d(Poly3DCollection(verts,facecolor='#000080',alpha=0.3))

ls1='ax.view_init(elev=30, azim=-135)'
ls2='xmin,xmax=-2,20'
ls3='ymin,ymax=-3,12'
ls4='zmin,zmax=-7,15'
ls=ls1+'\n'+ls2+'\n'+ls3+'\n'+ls4
ax.text2D(0, 1, ls, va='top',ha='left',transform=ax.transAxes,fontsize=fsz)

plt.savefig('fig_3.jpg',dpi=100)
plt.show()

作品例

ここで紹介した手法を用いて格子桁解析結果を示す断面力図を作成した事例を以下に示す。これの作図用コードは、格子桁解析の結果読み込みから始まり冗長なので省略する。こんな図も作れるんだ程度に見てほしい。もっと見やすくできないかについては更に経験値を積むことにするが、まずまずの出来か？（自画自賛）

以　上