Python, matplotlibでリアプノフ・フラクタルを描く

はじめに

2016年8月22日より，2ヶ月の予定でマレーシアに出張してきている．ホテル暮らしで休日は暇なので，久しぶりに趣味のプログラムを作ってみることにした．

フラクタル関係では，マンデルブロー，ブッダブロ，ジュリア集合などを描いたことがあるが，いずれもFortranで座標の色を計算し，GMTで出力させるものであったが，今回は全てPythonでやってみることにした．

作図機能としては，Python-matplotlibのヒートマップ描画機能（pcolor）を使っている．x座標，y座標，z値（作図上は色を示す値）をそれぞれ2次元配列で準備する必要があるが，作図用コーディングは非常にシンプルにでき，このような作図には便利である．

プログラム事例

以下のプログラムは，参考サイト(1)に記載のBASICプログラムをPythonに書き換えたものです．多少筆者の趣味で変更してある．

変化させる変数は以下のとおり

ab	a=0, b=1 として描きたい基本文字列（プログラム上では1次元配列）を作成
nm	1次元配列 *ab* の繰り返し数
a0, a1	x軸の範囲
b0, b1	y軸の範囲
irx, iry	x軸範囲およびy軸範囲の分割数

py_lyapunov0.py

import numpy as np
import matplotlib.pyplot as plt

ab=np.array([0,1])
nab=len(ab)
nm=10
a0=2
a1=4
b0=2
b1=4
irx=800
iry=600

x = np.linspace(a0,a1,irx+1)
y = np.linspace(b0,b1,iry+1)
X, Y = np.meshgrid(x, y)

z=np.empty((iry+1,irx+1))
for i in range(0,irx+1):
    a=a0+(a1-a0)/(irx)*i
    for j in range(0,iry+1):
        b=b0+(b1-b0)/(iry)*j
        s=0
        xx=0.5
        for n in range(0,nm):
            for m in range(0,nab):
                if ab[m]==0:
                    rr=a
                else:
                    rr=b
                xx=rr*xx*(1-xx)
                v=np.abs(rr*(1-2*xx))
                if 0<v: s=s+np.log(v)
        s=s/(nm*nab)
        if 2<s:
            z[j,i]=2
        elif s<-5:
            z[j,i]=-5
        else:
            z[j,i]=s

print(np.max(z))
print(np.min(z))

z=-1.0*z
plt.xlim(a0,a1)
plt.ylim(b0,b1)
plt.pcolor(X, Y, z, cmap=plt.cm.spectral)
plt.colorbar()
plt.show()

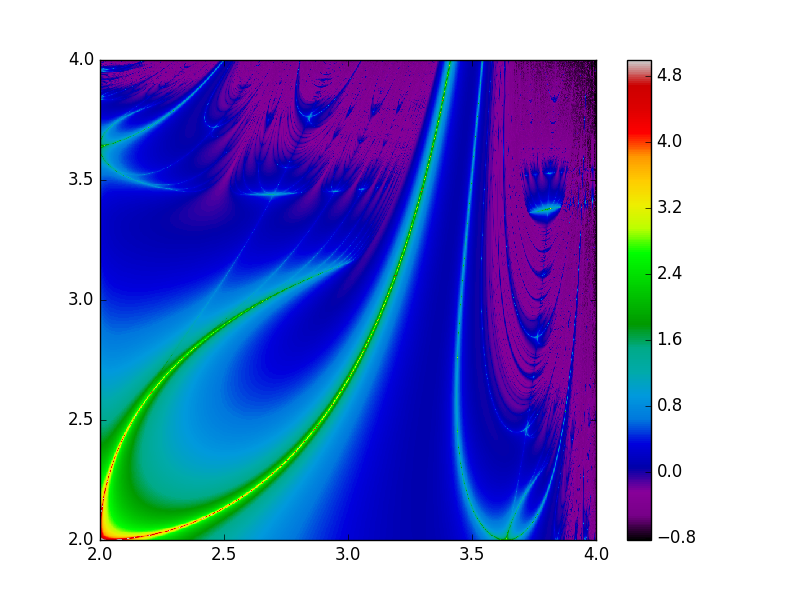
作図事例

上記プログラムに記載の変数により作図した事例を以下に示す．

参考サイト

(1) Lyapunov フラクタル作図プログラム事例
http://www.rowan.edu/colleges/csm/departments/math/facultystaff/osler/15.%20A%20quick%20look%20at%20Lyapunov%20space.pdf

(2) ヒートマップ実例
http://yoshihikomuto.hatenablog.jp/entry/2015/04/10/105615

(3) ヒートマップ基礎
http://d.hatena.ne.jp/y_n_c/20091122/1258904025

(4) リアプノフ・フラクタル（Wikipedia）
[https://ja.wikipedia.org/wiki/%E3%83%AA%E3%82%A2%E3%83%97%E3%83%8E%E3%83%95%E3%83%BB%E3%83%95%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%AB]
(https://ja.wikipedia.org/wiki/%E3%83%AA%E3%82%A2%E3%83%97%E3%83%8E%E3%83%95%E3%83%BB%E3%83%95%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%AB)

以上