LoginSignup
19
29

More than 5 years have passed since last update.

@damyarou

Pythonで２次元非定常熱伝導解析

Last updated at Posted at 2016-11-28

概要

Pythonで２次元非定常熱伝導解析プログラムを作ってみました．
要素は，浸透流解析と同じ，４節点４ガウス積分点を有するアイソパラメトリック要素です．

非定常熱伝導解析のための有限要素式

ここでは，以下の要素の有限要素式を用いています．

$$
[\boldsymbol{k}]\{\boldsymbol{\phi}\}+[\boldsymbol{c}]\left\{\cfrac{\partial \boldsymbol{\phi}}{\partial t}\right\}=\{\boldsymbol{f}\}
$$

$$
\begin{align}
&[\boldsymbol{k}]=\int_A \kappa\left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA
+\int_s \alpha_c[\boldsymbol{N}]^T [\boldsymbol{N}]ds \\
&[\boldsymbol{c}]=\int_A \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]dA \\
&{\boldsymbol{f}}=\int_A \dot{Q}[\boldsymbol{N}]^T dA+\int_s \alpha_c T_c [\boldsymbol{N}]^T ds
\end{align}
$$

  • $[\boldsymbol{k}]$ : 熱伝導マトリックス．第２項は熱伝達境界によるもの
  • $[\boldsymbol{c}]$ : 熱容量マトリックス
  • ${\boldsymbol{\phi}}$ : 節点温度ベクトル
  • ${\boldsymbol{f}}$ : 熱流束ベクトル．第１項は発熱によるもの，第２項は熱伝達によるもの
  • $[\boldsymbol{N}]$ : 内挿関数行列
  • $\kappa$, $\rho$, $c$ : 熱伝導率，密度，比熱
  • $\alpha_c$, $T_c$ : 熱伝達率，熱伝達境界の外部温度
  • $\dot{Q}$ : 発熱率
  • $\int_A$, $\int_S$ : 要素面積および要素辺での積分

発熱の考慮

コンクリートの熱伝導解析を意識して，コンクリートの断熱温度上昇特性を入れられるようにしてあります．

$$
T(t)=T_k (1-e^{-\alpha t})
$$

ここに，$T_k$は最終温度上昇量，$\alpha$は発熱速度を示すパラメータです．
上式を用い，発熱量$Q$および発熱率$\dot{Q}$は以下のように表現できます．
$$
\begin{equation}
Q=\rho \cdot c \cdot T(t) \qquad \rightarrow \qquad \dot{Q}=\rho \cdot c \cdot T_k \cdot \alpha \cdot e^{-\alpha t}
\end{equation}
$$

時間離散化手法

非定常有限要素式を解く上での時間離散化手法として,Crank-Nicolson 差分式を用いています．
実際には差分式を用い，時刻$t$における既知ベクトルを用いて$t+\Delta t$における節点温度を逐次求めていきます．
記号を大文字にしているのは，解析範囲全体のマトリックス・ベクトルを示すためです．

$$
\begin{equation}
\left(\frac{1}{2}[\boldsymbol{K}]+\frac{1}{\Delta t}[\boldsymbol{C}]\right){\boldsymbol{\Phi}(t+\Delta t)}
=\left(-\frac{1}{2}[\boldsymbol{K}]+\frac{1}{\Delta t}[\boldsymbol{C}]\right){\boldsymbol{\Phi}(t)}+\frac{{\boldsymbol{F}(t+\Delta t)}+{\boldsymbol{F}(t)}}{2}
\end{equation}
$$

要素の材料特性は時間により変化しない設定をしているため，時間ステップ計算では，numpy.linalg.inv(A)で一回だけ逆行列を求め，これを記憶して各時刻の温度履歴を計算しています．

境界条件

  • 境界条件は，断熱，温度固定，熱伝達を考慮できます．
  • 境界条件として何も入れなければ断熱境界になります．
  • 温度固定境界の場合は，節点温度を指定します．
  • 熱伝達境界の場合は，要素の辺および外部温度を指定します．

使えるか？

使えるかという点では，400要素，441自由度，計算時間ステップ数1000回で38秒程度．評価は個人のセンスによりますが，私の場合は待てない時間ではない．ちなみにFortranでは同じモデルの計算が1.6秒で完了します．

プログラム

FEMプログラムと同時に，作図プログラムを作りました．言語はPythonですが，温度履歴グラフはmatplotlibを，３次元温度分布図はGMT(Generic Mapping Tools)で描画しています．matplotlibの３次元グラフはあまりかっこよくないので．

プログラムおよび入力データ事例は，Gistに貼り付けたものへのリンクで示します．

実行用スクリプト

FEM計算実行スクリプト

a_py.txt
python3 py_fem_heat.py inp_div20_model.txt inp_div20_thist.txt out_div20.txt

作図実行スクリプト

Pythonによる温度履歴グラフ，GMTによる３次元温度分布図を作成するためのスクリプト

a_fig.txt
python3 py_heat_2D.py out_11_div20_10.txt
python3 py_heat_3D.py out_11_div20_10.txt
bash _a_gmt_3D.txt
mogrify -trim -density 300 -bordercolor 'transparent' -border 10x10 -format png *.eps
rm *.eps

TeXによるpdf作成とImageMagickによるpng画像作成

TeXでpdfを作成後，ImageMagickにより余白を削除（調整）したpng画像を作成するスクリプト

a_tex.txt
platex tex_fig.tex
dvipdfmx -p a3 tex_fig.dvi

convert -trim -density 400 tex_fig.pdf -bordercolor 'transparent' -border 20x20 -quality 100 tex_fig.png
tex_fig.tex

TeX文書

８枚のpng画像を並べてA3用紙に配置するためのTeX文書

tex_fig.tex
\documentclass[english]{jsarticle}
\usepackage[a3paper,top=25mm,bottom=25mm,left=25mm,right=25mm]{geometry}
\usepackage[dvipdfmx]{graphicx}
\pagestyle{empty}

\begin{document}

\begin{center}
\begin{tabular}{cc}
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_0.png}\end{minipage}&
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_1.png}\end{minipage}\\
 & \\
 & \\
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_2.png}\end{minipage}&
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_3.png}\end{minipage}\\
 & \\
 & \\
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_4.png}\end{minipage}&
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_5.png}\end{minipage}\\
 & \\
 & \\
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_6.png}\end{minipage}&
\begin{minipage}{12.0cm}\vspace{0.2zh}\includegraphics[width=12.0cm,bb={0 0 1900 1122}]{_fig_gmt_xyz_7.png}\end{minipage}\\
\end{tabular}
\end{center}

\end{document}

入力データ書式

入力データとして２つのファイルを用います．

１つは，モデルデータ．節点数，要素数などの基本諸量，材料特性，要素ー節点関係，節点座標，境界条件などを入力します．

もう１つは，温度指定境界・熱伝達境界の外部温度の時刻歴データファイルです．情報量が多くなるので，モデルデータとは分離して入力するようにしました．

モデルデータ

npoin  nele  nsec  kot  koc  delta          # Basic values for analysis
Ak  Ac  Arho  Tk  Al                        # Material properties
     ....(1 to nsec)....                    #
node-1  node-2  node-3  node-4  isec        # Element connectivity, Material set number
     ....(1 to nele)....                    # (counterclockwise order of node numbers)
x  y  T0                                    # Coordinates of node, initial temperature of node
     ....(1 to npoin)....                   # (x: right-direction, y: upward direction)
nokt                                        # Node number of temperature given boundary
     ....(1 to kot)....                     # (Omit data input if kot=0)
nekc_0  nekc_1  alphac                      # Element number, node number defined side, heat transfer rate
     ....(1 to koc)....                     # (Omit data input if koc=0)
n1out                                       # Number of nodes for output of temperature time history
n1node_1   ....(1 line input)....           # Node number for above
n2out                                       # frequency of output of temperatures of all nodes
n2step_1  ....(1 line input)....            # Time step number for above
                                            # (Omit data input if ntout=0)
npoin, nele, nsec 節点数，要素数，材料特性数
kot, koc 温度指定境界節点数，熱伝達境界要素辺数
delta 計算時間間隔
Ak, Ac, Arho 熱伝導率，比熱，密度
Tk, Al 最高断熱上昇温度，発熱速度パラメータ
x, y, T0 節点x座標，節点y座標，節点初期温度
nokt 温度指定境界節点番号
nekc_0, nekc_1, alphac 熱伝達境界を有する要素番号，熱伝達境界要素辺の節点番号，熱伝達境界の熱伝達率
n1out 全時刻歴を出力する節点数
n1node 全時刻歴を出力する節点番号
n2out 全節点温度を出力する時間ステップ数
n2step 全節点温度を出力する時間ステップ番号

熱伝達境界では，要素の辺を指定する必要があります．このため，熱伝達境界辺を有する要素番号および辺を指定する節点番号を指定します．FEMでは要素を指定する節点番号は，反時計回りに入力するので，辺を構成する最初の節点番号を入力すれば，その辺を特定することができます．

温度指定境界・熱伝達境界外部温度データ

   1   TE[1] ... TE[kot] TC[1] ... TC[koc]   # data of 1st time step
   2   TE[1] ... TE[kot] TC[1] ... TC[koc]   # data of 2nd time step
   3   TE[1] ... TE[kot] TC[1] ... TC[koc]   #
    ....(repeating until end time).....      # data is read step by step
itime  TE[1] ... TE[kot] TC[1] ... TC[koc]   #
  • kot: 温度指定境界節点数
  • koc: 熱伝達境界要素辺数
  • TE[1~kot]: 温度指定境界での温度履歴
  • TC[1~koc]: 熱伝達境界での外部温度履歴

出力データ書式

npoin  nele  nsec   kot   koc           delta  niii n1out n2out
   25    16     1     0    16   1.0000000e+00   101     5     0
  sec              Ak              Ac            Arho              Tk              Al
    1   2.5000000e+00   2.8000000e-01   2.3500000e+03   4.0000000e+01   2.0000000e-01
 node               x               y          tempe0  Tfix
    1  -5.0000000e-01  -5.0000000e-01   2.0000000e+01     0
    2  -5.0000000e-01  -2.5000000e-01   2.0000000e+01     0
    3  -5.0000000e-01   0.0000000e+00   2.0000000e+01     0
..... (omit) .....
0
   23   5.0000000e-01   0.0000000e+00   2.0000000e+01     0
   24   5.0000000e-01   2.5000000e-01   2.0000000e+01     0
   25   5.0000000e-01   5.0000000e-01   2.0000000e+01     0
 nek0  nek1 alphac         
    1     1   1.0000000e+01
    5     6   1.0000000e+01
    9    11   1.0000000e+01
   13    16   1.0000000e+01
   13    21   1.0000000e+01
   14    22   1.0000000e+01
   15    23   1.0000000e+01
   16    24   1.0000000e+01
   16    25   1.0000000e+01
   12    20   1.0000000e+01
    8    15   1.0000000e+01
    4    10   1.0000000e+01
    4     5   1.0000000e+01
    3     4   1.0000000e+01
    2     3   1.0000000e+01
    1     2   1.0000000e+01
 elem     i     j     k     l   sec
    1     1     6     7     2     1
    2     2     7     8     3     1
    3     3     8     9     4     1
    4     4     9    10     5     1
    5     6    11    12     7     1
    6     7    12    13     8     1
    7     8    13    14     9     1
    8     9    14    15    10     1
    9    11    16    17    12     1
   10    12    17    18    13     1
   11    13    18    19    14     1
   12    14    19    20    15     1
   13    16    21    22    17     1
   14    17    22    23    18     1
   15    18    23    24    19     1
   16    19    24    25    20     1
  iii           ttime         Node_11         Node_12         Node_13         Node_14         Node_15
    0   0.0000000e+00   2.0000000e+01   2.0000000e+01   2.0000000e+01   2.0000000e+01   2.0000000e+01
    1   1.0000000e+00   2.5712484e+01   2.7416428e+01   2.7023876e+01   2.7416428e+01   2.5712484e+01
    2   2.0000000e+00   2.8833670e+01   3.3625990e+01   3.2820487e+01   3.3625990e+01   2.8833670e+01
..... (omit) .....
   98   9.8000000e+01   1.1182079e+01   1.2141098e+01   1.2494074e+01   1.2141098e+01   1.1182079e+01
   99   9.9000000e+01   1.1140143e+01   1.2065139e+01   1.2405593e+01   1.2065139e+01   1.1140143e+01
  100   1.0000000e+02   1.1099694e+01   1.1991874e+01   1.2320250e+01   1.1991874e+01   1.1099694e+01
n=25  time=0.147 sec
niii 計算ステップ数（初期温度を含む）
Tfix 節点温度指定の有無（０：温度指定なし，１：温度指定あり）
iii, ttime, Node_x 時間ステップ，時刻，温度履歴を出力する節点番号
これ以降は，各時刻での温度履歴が出力される

出力事例

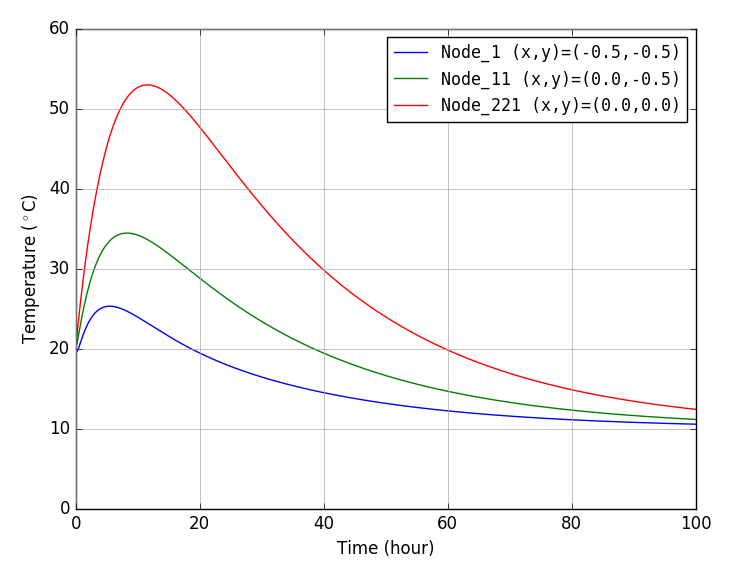
matplotlibで作成した温度履歴グラフ

_fig_tem_his.png

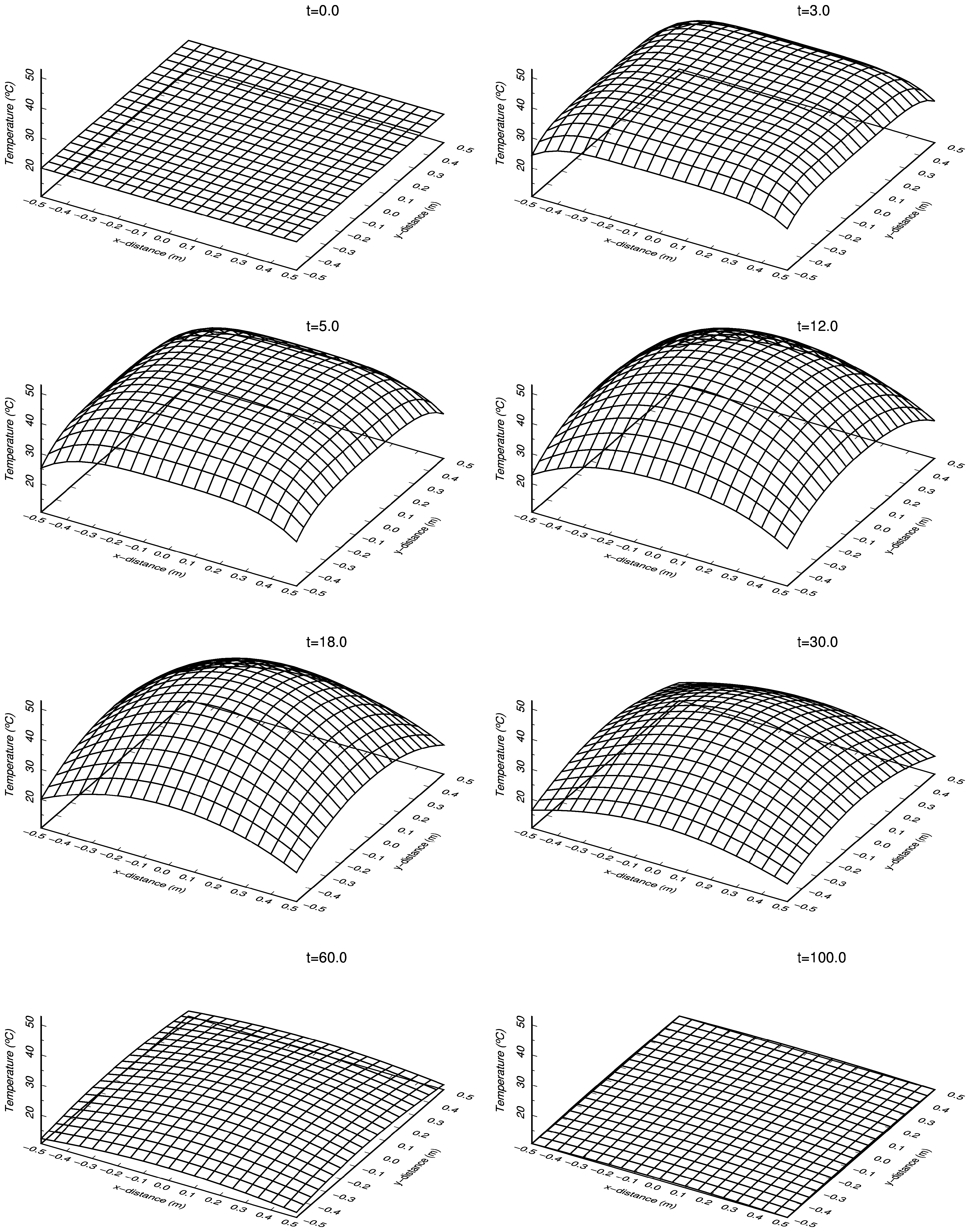
GMTで作成した各時刻の温度分布図

時間の単位は，hourです．
tex_fig.png

以　上

19
29
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
19
29